próbny egzamin ósmoklasisty 2024, egzamin ósmoklasisty matematyka, arkusz matematyka 2024, przygotowanie do egzaminu, test ósmoklasisty online, próbne arkusze egzaminacyjne, ósmoklasista materiały edukacyjne, egzamin grudzień 2024, matematyka próbny test, arkusze PDF do pobrania.
próbny egzamin ósmoklasisty 2024, egzamin ósmoklasisty matematyka, arkusz matematyka 2024, przygotowanie do egzaminu, test ósmoklasisty online, próbne arkusze egzaminacyjne, ósmoklasista materiały edukacyjne, egzamin grudzień 2024, matematyka próbny test, arkusze PDF do pobrania.
PRÓBNY EGZAMIN ÓSMOKLASISTY Z MATEMATYKI CKE 2024
100%








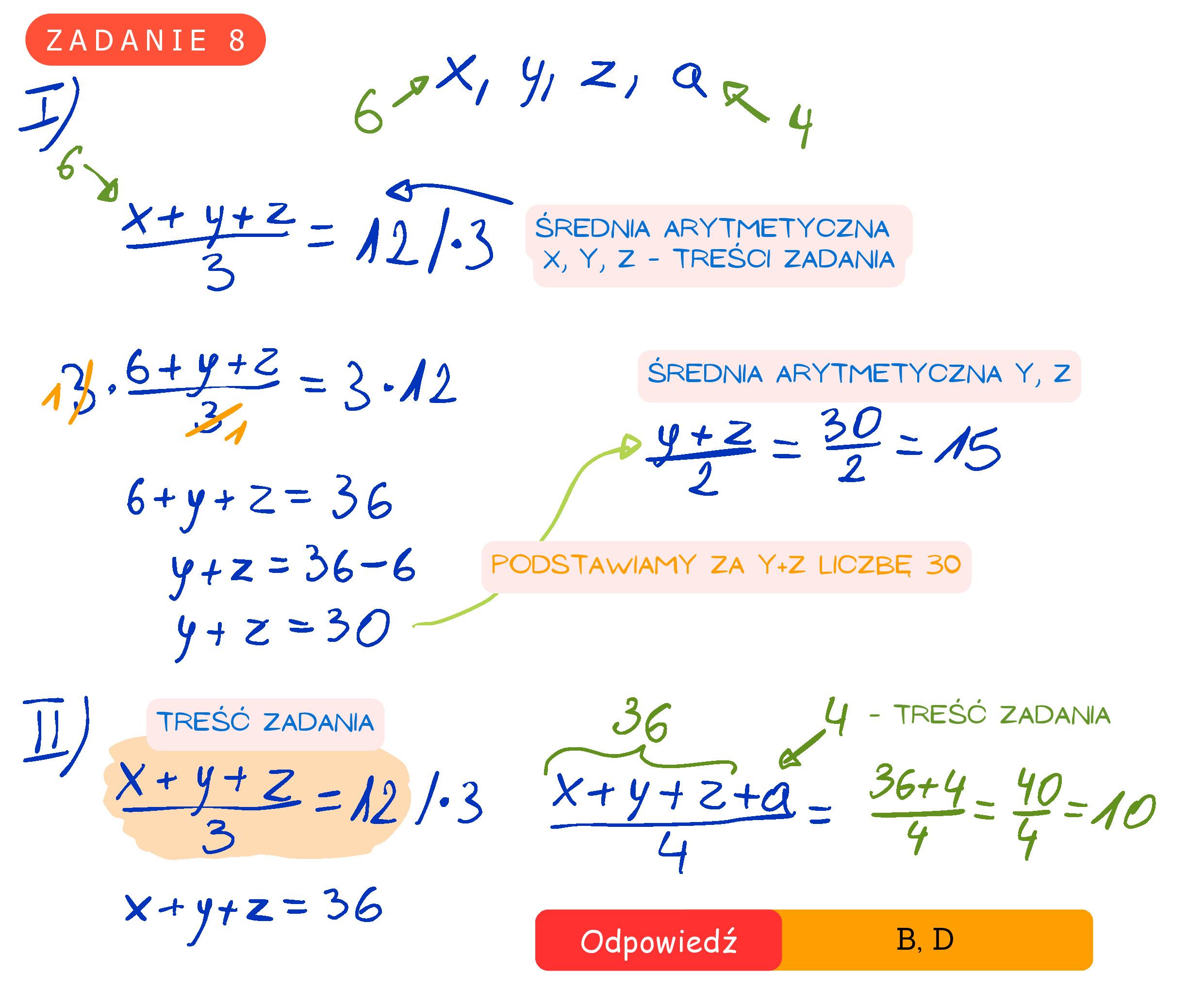
![Dane są cztery liczby: x, y, z, a. Wiadomo, że x =6, a =4 oraz średnia arytmetyczna
trzech liczb x, y, z jestrówna 12.
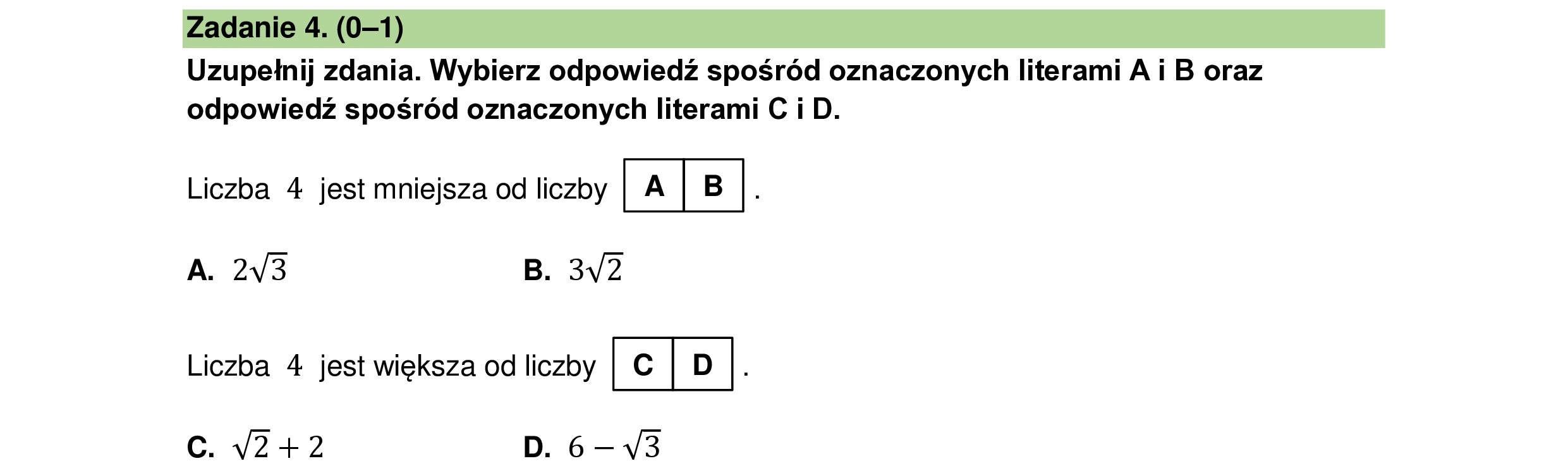
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz
odpowiedź spośród oznaczonych literami C i D.
Średnia arytmetyczna dwóch liczb y i z jest równa [a]B].
A. 6 B. 15
Średnia arytmetyczna czterech liczb: x, y, z, a, jest równa e|p].
C. 8 D. 10](https://firebasestorage.googleapis.com/v0/b/zdalnaszkola-images.appspot.com/o/egzamin_%C3%B3smoklasisty%2F2024_PRÓBNY_CKE_ZADANIE_8.jpg?alt=media)











PRÓBNY EGZAMIN ÓSMOKLASISTY Z MATEMATYKI CKE 2024
100%













![Dane są cztery liczby: x, y, z, a. Wiadomo, że x =6, a =4 oraz średnia arytmetyczna
trzech liczb x, y, z jestrówna 12.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz
odpowiedź spośród oznaczonych literami C i D.
Średnia arytmetyczna dwóch liczb y i z jest równa [a]B].
A. 6 B. 15
Średnia arytmetyczna czterech liczb: x, y, z, a, jest równa e|p].
C. 8 D. 10](https://firebasestorage.googleapis.com/v0/b/zdalnaszkola-images.appspot.com/o/egzamin_%C3%B3smoklasisty%2F2024_PRÓBNY_CKE_ZADANIE_8.jpg?alt=media)
























































