MATEMATYKA 2023 SIERPIEN POPRAWKOWA PODSTAWOWA
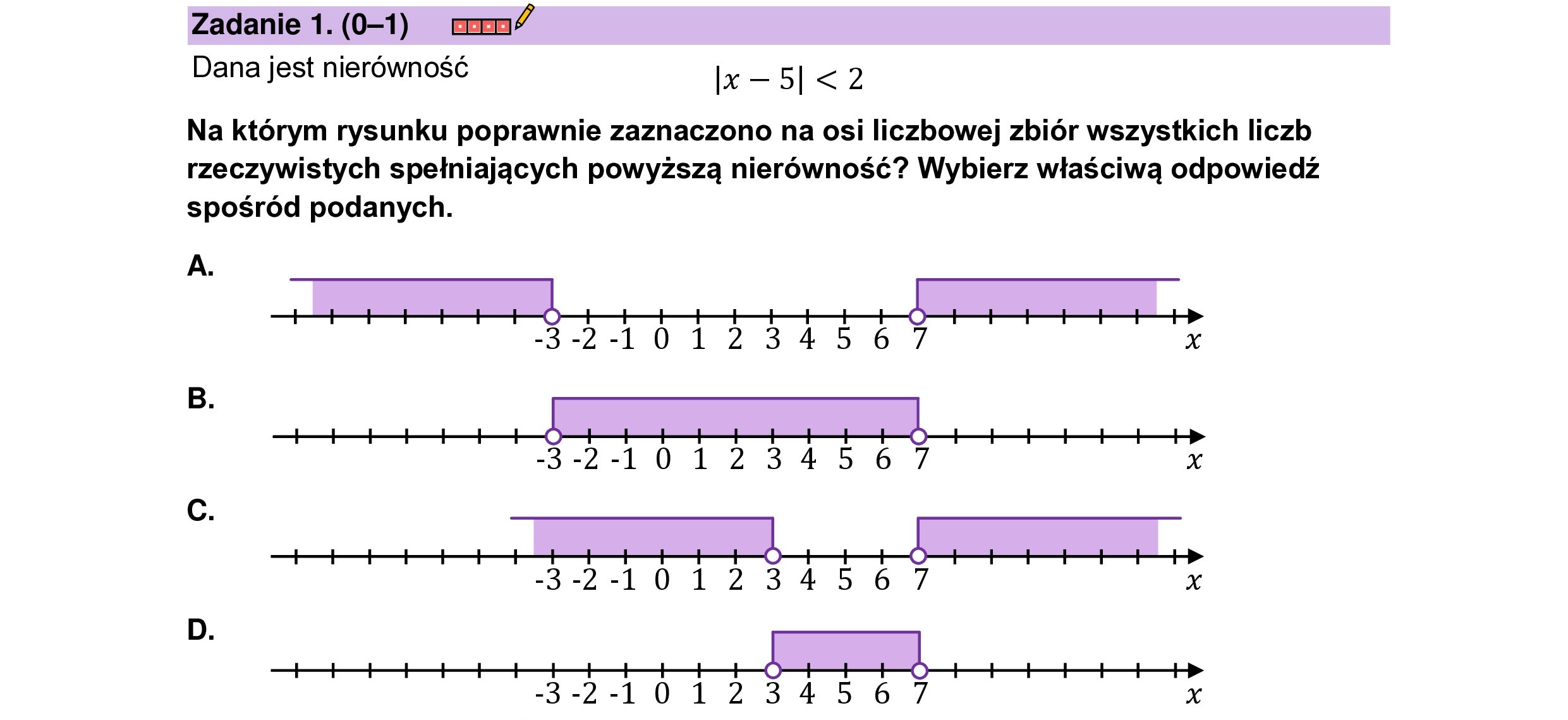
Zadanie 1.(0-1) crrm” Dana jest nierówność |x-5|<2 Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność? Wybierz właściwą odpowiedź spośród podanych. A. -3-2-10 1234567 x B. -3-2-10 1234567 £4 |e2 -3-2-10 1234567 x D. -3-2-10 1234567 x


Zadanie 2. (0-1) err” Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba 3Vv45 — v20 jest równa 1 1 A. (7-5) B. 5? C. 7 D „ fo 5 NI


Zadanie 3. (0—1) err Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba logos 1 — logos 5 jest równa A. (- 2) B. (-3) e) AIR U NI


Zadanie 4. (0—2) Wykaż, że dla każdej liczby naturalnej n > 1 liczba 3n* + 18n* + 15n jest podzielna przez 6.


Zadanie 5. (0-1) err” Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. —1 Wartość wyrażenia — — ' 81 jest równa 9 A. ę B. (-3) Cc. 3 D. (—3)


Zadanie 6. (0-1) crrmó Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wartość wyrażenia (2 — V3) — (V3— 2) jest równa A. (-2v3) B. 0 Cc. 6 D. 8V3


Zadanie 7. (0—1) err Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Dla każdej liczby rzeczywistej x różnej od 0 wartość wyrażenia m — x jest równa wartości wyrażenia 1 1-x A. x B. "2x 1-2x2 1 2x


Zadanie 8. (0-1) crrm? Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. (x2—3x)(x2+1) x2—25 A. jedno rozwiązanie. Równanie = (0 wzbiorze liczb rzeczywistych ma dokładnie B. dwa rozwiązania. C. trzy rozwiązania. D. cztery rozwiązania.

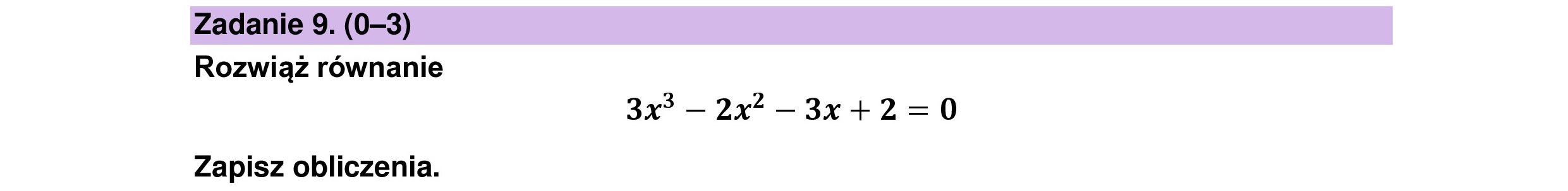
Zadanie 9. (0—3) Rozwiąż równanie 3x — 2x” —3x+2=0 Zapisz obliczenia.


Zadanie 10. (0-1) err Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. W kartezjańskim układzie współrzędnych (x,y), punkt (—8,6) jest punktem przecięcia prostych o równaniach A. 2x+3y=2 | —x ty = —14. B. 3x +2y = —12 i 2x +y=10. C. x+ty=-2 | x —2Ży=4. D. xy =—14 | —2x +y=22.


Zadanie 11. (0-1) err Miejscem zerowym funkcji liniowej f jest liczba 1. Wykres tej funkcji przechodzi przez punkt (—1, 4). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wzór funkcji f ma postać b 3 C. f(x) = —2x +2 D. f(x) = —3x +1 A. f(X) =-zx+1 B. f(X) = -3x+


Zadanie 12. (0-1) prrni Funkcja f_ jest określona dla każdej liczby rzeczywistej x wzorem f(x) = Żar » gdzie k jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek f(1) = 2. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wartość współczynnika k we wzorze tej funkcji jest równa A. (—3) B. 3 c. (—4) D. 4


Zadanie 13. (0-1) crrm* Funkcja kwadratowa f jest określona wzorem f(x) = (x — 13)? — 256. Jednym z miejsc zerowych tej funkcji jest liczba (—3). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Drugim miejscem zerowym funkcji f jest liczba A. (—29) B. (—23) C. 23 D. 29

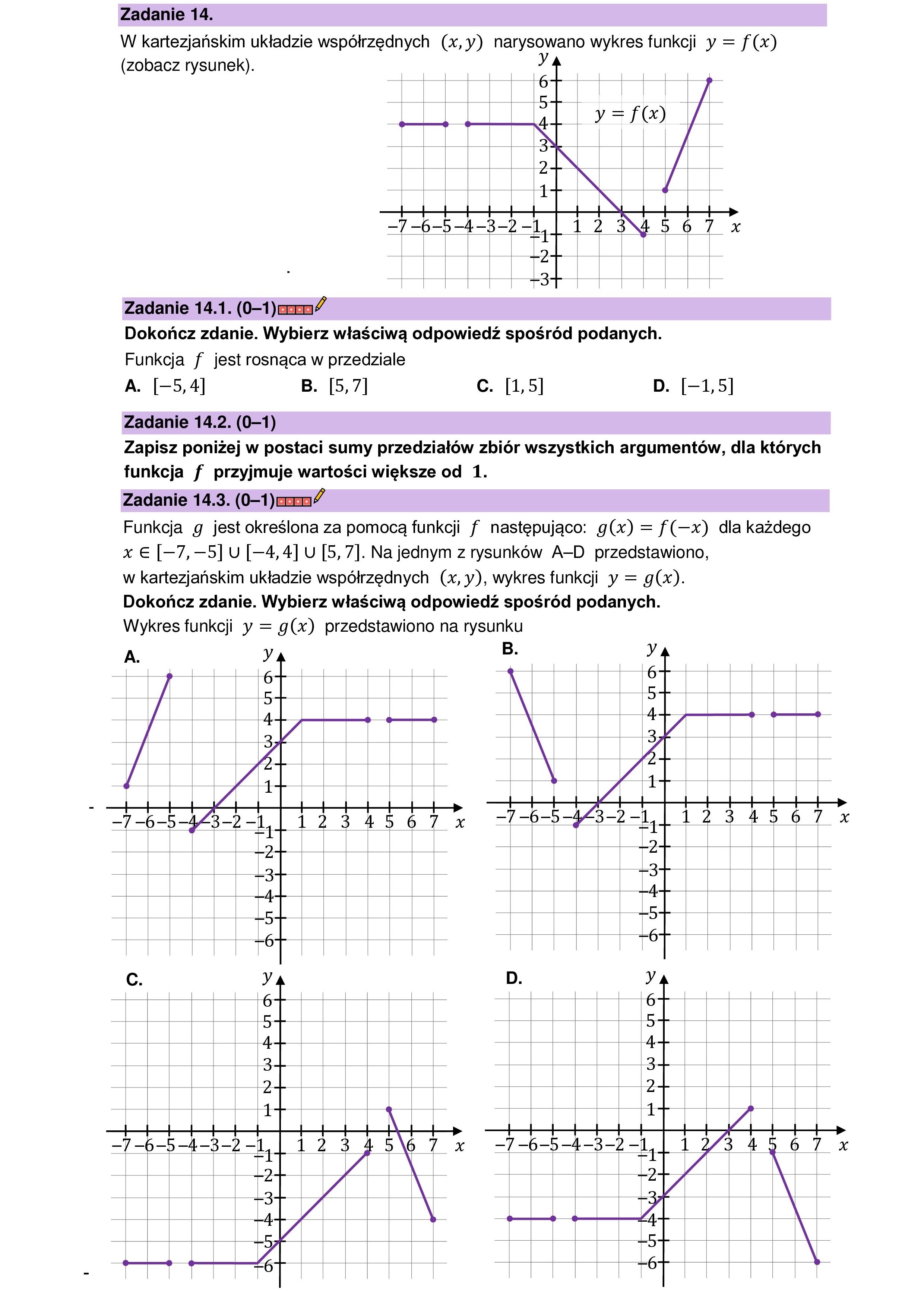
Zadanie 14. W kartezjańskim układzie współrzędnych (x,y) narysowano wykres funkcji y = f(x) (zobacz rysunek). y Zadanie 14.1. (0-1)crrm7 Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Funkcja f jest rosnąca w przedziale A. [-5,4] B. [5,7] c. [1,5] D. [—1,5] Zadanie 14.2. (0—1) Zapisz poniżej w postaci sumy przedziałów zbiór wszystkich argumentów, dla których funkcja f przyjmuje wartości większe od 1. Zadanie 14.3. (0-1)crrm* Funkcja g jest określona za pomocą funkcji f następująco: g(x) = f(—x) dla każdego x € [—7,-5] U [—4,4] U [5,7]. Na jednym z rysunków A-D przedstawiono, w kartezjańskim układzie współrzędnych (x, y), wykres funkcji y = g(x). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wykres funkcji y = g(x) przedstawiono na rysunku A. y E. y | 6 SZSZSZ || 16 3 3 1 1 —7-6-5-4/3-—2-1, | 12 3 4567 x 77-6-5-935-2-1,| 12 3 67 x 15 [12 15 |—5


Zadanie 15. (0—2) Funkcje A,B,C, D,E oraz F są określone dla każdej liczby rzeczywistej x. Wzory tych funkcji podano poniżej. Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A-F i wpisz te litery w wykropkowanych miejscach. Przedział (—oo, 2] jest zbiorem wartości funkcji ............. EFEZ mamus s A. A(x) = —(x — 3)7 +2 D. D(x) = (x — 2)? B. B(x)=1x* +2 E. E(x) = 2x? —8x + 10 c. C(x) =—5(x — 2)? F. F(x) =—2x? + 4x


Zadanie 16. (0-1) prrni Ciąg (a,„) jest określony wzorem a, = (—1)”: m dla każdej liczby naturalnej n > 1. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Trzeci wyraz tego ciągu jest równy A. 2 B. (-2) c. 3 D. (—1)


Zadanie 17. (0-1) err Dany jest ciąg geometryczny (a,), określony dla każdej liczby naturalnej n > 1. Pierwszy wyraz tego ciągu jest równy 128, natomiast iloraz ciągu jest równy (-;). Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F — jeśli jest fałszywe. Wyraz 4023 jest liczbą ujemną. P F Różnica a3 — A jest równa 96.


Zadanie 18. (0—2) Ciąg (3x? + 5x, x?, 20 — x?) jest arytmetyczny. Oblicz x. Zapisz obliczenia.


Zadanie 19. (0-1) crrmó Kąt a jestostryi cosa = z, Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Sinus kąta a jest równy A. Es B. 25 /6 49 7 |e2 49 D. JI OT


Zadanie 20. (0-1) crrmó Trapez T, , o polurównym 52 iobwodzie 36, jest podobny do trapezu T;, . Pole trapezu T, jestrówne 13. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Obwód trapezu T> jest równy A. 18 B. 9 c. | D. Sa


Zadanie 21. (0-1) crrm* Koło ma promień równy 3. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Obwód wycinka tego koła o kącie środkowym 30” jest równy 3 1 A. 47 B. 7" G. LEK D. 51 +6


Zadanie 22. (0-1) rrrm4 W okręgu O kątśrodkowy E oraz kąt wpisany a są oparte na tym samym łuku. Kąt 8 ma miarę o 40” większą od kąta a. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Miara kąta 5 jest równa A. 40? B. 80? c. 100” D. 120?


Zadanie 23. (0-1) zrm W trójkącie ABC długość boku AC jestrówna 3, a długość boku BC jest równa 4. Dwusieczna kąta ACB przecina bok AB w punkcie D. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Stosunek |AD| : |DB| jest równy A. 4:3 B. 4:7 C. 3:4 D. 3:7

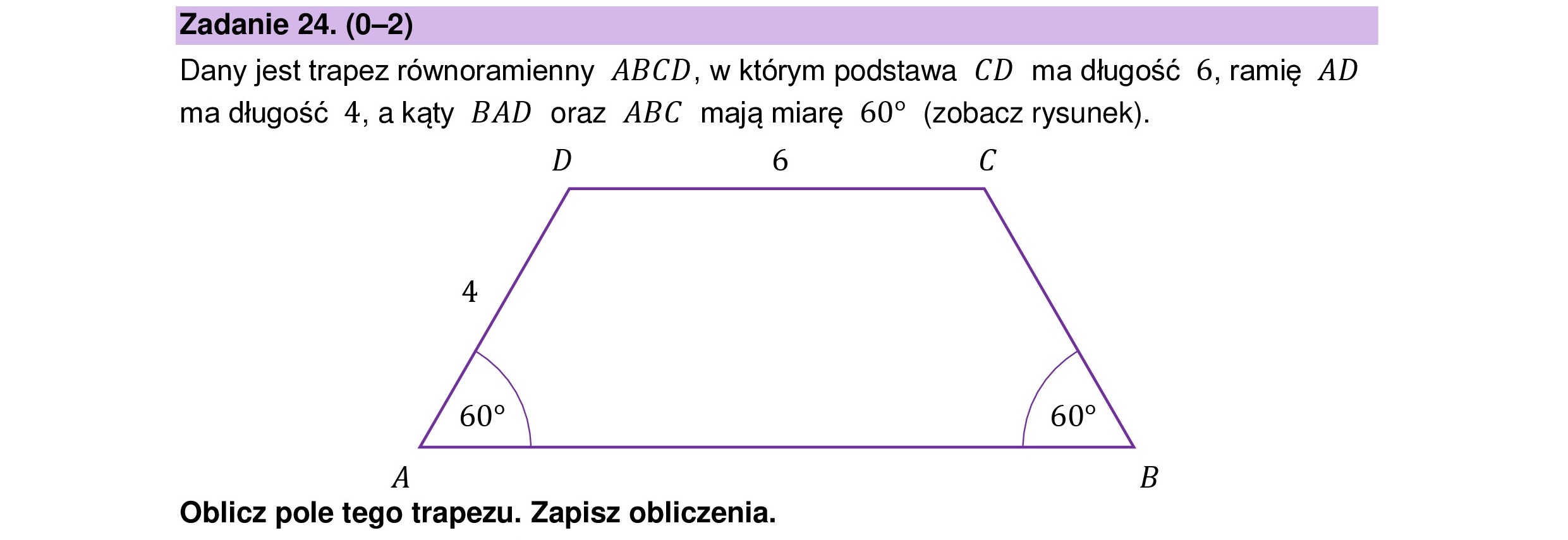
Zadanie 24. (0—2) Dany jest trapez równoramienny ABCD, w którym podstawa CD ma długość 6, ramię AD ma długość 4, akąty BAD oraz ABC mają miarę 60” (zobacz rysunek). D 6 C 4 A (a A B Oblicz pole tego trapezu. Zapisz obliczenia.


Zadanie 25. (0-1) crrm4 W kartezjańskim układzie współrzędnych (x,y) dane są prosta k o równaniu y = qx -3 oraz punkt P = (12, —1). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Prosta przechodząca przez punkt Pi równoległa do prostej k ma równanie A.y=—qx+8 B. y= qx—10 C.y= 3x —17 D.y=-gx+15 4


Zadanie 26. (0-1) crrm* W kartezjańskim układzie współrzędnych (x,y) dany jest okrąg O o środku S = (—1,2) i promieniu 3. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Okrąg O jest określony równaniem A. (x—1)?+(y +2)? =9 B. (x—1)7+(y+2)7=3 C. (x +1)” +(y-2)7=9 D. (x+1)7+(y-2)7=3


Zadanie 27. (0-1) crrm” W kartezjańskim układzie współrzędnych (x,y) proste o równaniach: 1 . = 3x +6 e = —43x + 6 . =——x— y y y J3% Ży przecinają się w punktach, które są wierzchołkami trójkąta KLM. Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3. Trójkąt KLM jest oś Ox przechodzi przez jeden z wierzchołków 1. | tego trójkąta i środek jednego z boków tego A. | równoramienny, trójkąta ponieważ | 2. | dwie z tych prostych są prostopadłe. B. | prostokątny, 3. |oś Oy zawiera dwusieczną tego trójkąta.


Zadanie 28. (0-1) err W kartezjańskim układzie współrzędnych (x,y) punkt A = (—1, —4) jest wierzchołkiem równoległoboku ABCD. Punkt S = (2,2) jest środkiem symetrii tego równoległoboku. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Długość przekątnej AC równoległoboku ABCD jest równa A. V5 B. 2Y5 Cc. 3Y5 D. 6Y5


Zadanie 29. Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Zadanie 29.1. (0-1)rrrm* Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Pole powierzchni całkowitej tego graniastosłupa jest równe A. 216 + 18V3 B. 216 + 54V3 C. 216 + 216V3 D. 216 + 108V3 Zadanie 29.2. (0—1) Oblicz cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa. Zapisz obliczenia.


Zadanie 30. (0-1) rrr Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wszystkich liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym cyfry się nie powtarzają, jest A. 9:10:10:10:10 B. 9-9-9-9 C. 10:9:8:7 D. 9:9:8:7


Zadanie 31. (0-2) Ze zbioru pięciu liczb f1, 2, 3,4,5) losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że obie wylosowane liczby są nieparzyste. Zapisz obliczenia.

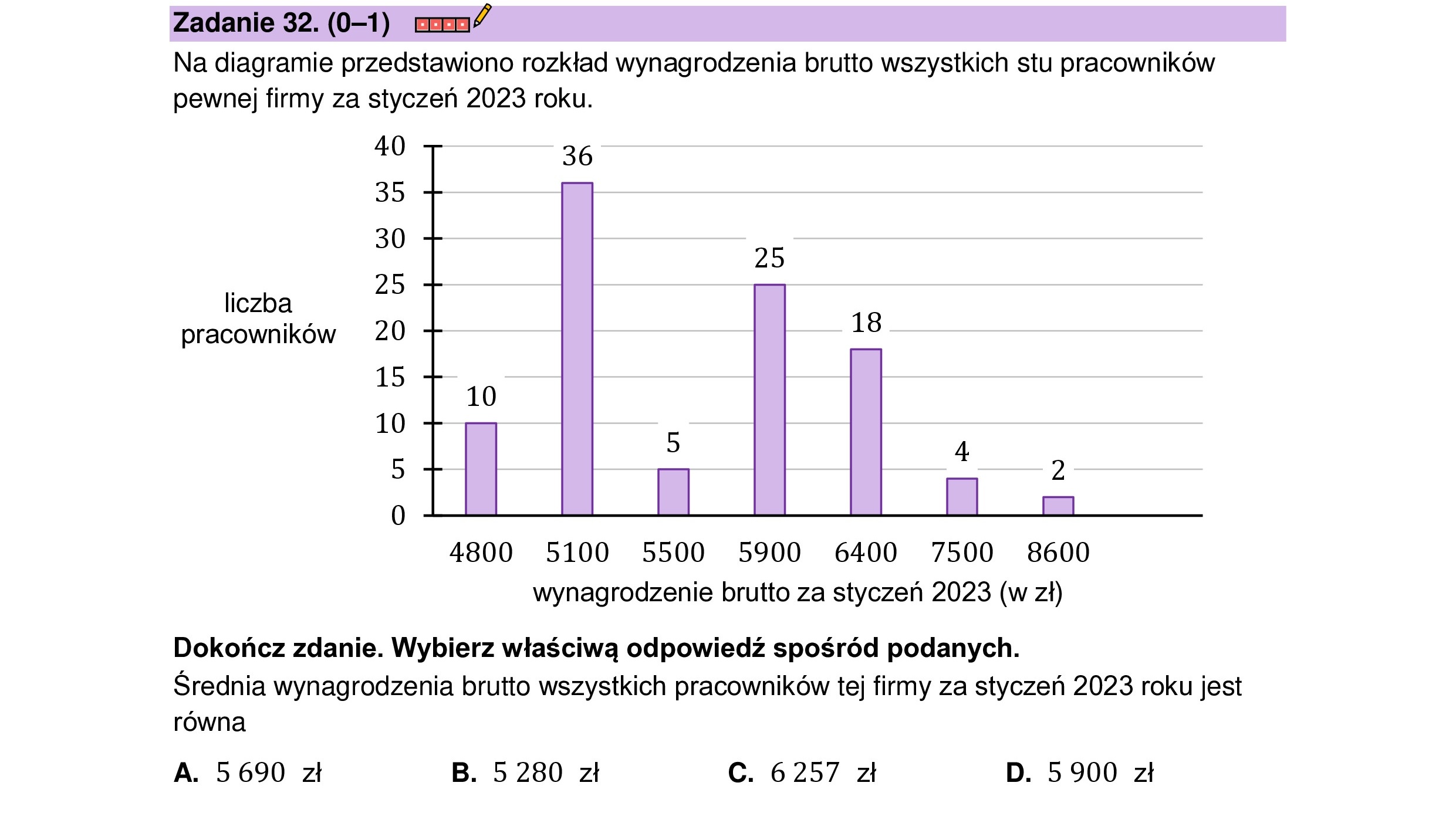
Zadanie 32. (0-1) crrm* Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich stu pracowników pewnej firmy za styczeń 2023 roku. 30 36 35 30 liczba 25 pracowników 20 15 10 5 2 0 25 18 10 4800 5100 5500 5900 6400 7500 8600 wynagrodzenie brutto za styczeń 2023 (w zł) Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Średnia wynagrodzenia brutto wszystkich pracowników tej firmy za styczeń 2023 roku jest równa A. 5690 zł B. 5 280 zł C. 6257 zł D. 5900 zł


Zadanie 33. (0-4) Zakład stolarski produkuje krzesła, które sprzedaje po 196 złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że: e przychód P (w złotych) ze sprzedaży x krzeseł można opisać funkcją P(x) = 196x e koszt K (w złotych) produkcji x krzeseł dziennie można opisać funkcją K(x) = 4x? + 4x + 240 Dziennie w zakładzie można wyprodukować co najwyżej 30 krzeseł. Oblicz, ile krzeseł powinien dziennie sprzedawać zakład, aby zysk ze sprzedaży krzeseł wyprodukowanych przez ten zakład w ciągu jednego dnia był możliwie największy. Oblicz ten największy zysk. Zapisz obliczenia. Wskazówka: przyjmij, że zysk jest różnicą przychodu i kosztów.

MATEMATYKA 2023 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1.(0-1) crrm” Dana jest nierówność |x-5|<2 Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność? Wybierz właściwą odpowiedź spośród podanych. A. -3-2-10 1234567 x B. -3-2-10 1234567 £4 |e2 -3-2-10 1234567 x D. -3-2-10 1234567 x


Zadanie 2. (0-1) err” Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba 3Vv45 — v20 jest równa 1 1 A. (7-5) B. 5? C. 7 D „ fo 5 NI


Zadanie 3. (0—1) err Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba logos 1 — logos 5 jest równa A. (- 2) B. (-3) e) AIR U NI


Zadanie 4. (0—2) Wykaż, że dla każdej liczby naturalnej n > 1 liczba 3n* + 18n* + 15n jest podzielna przez 6.


Zadanie 5. (0-1) err” Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. —1 Wartość wyrażenia — — ' 81 jest równa 9 A. ę B. (-3) Cc. 3 D. (—3)


Zadanie 6. (0-1) crrmó Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wartość wyrażenia (2 — V3) — (V3— 2) jest równa A. (-2v3) B. 0 Cc. 6 D. 8V3


Zadanie 7. (0—1) err Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Dla każdej liczby rzeczywistej x różnej od 0 wartość wyrażenia m — x jest równa wartości wyrażenia 1 1-x A. x B. "2x 1-2x2 1 2x


Zadanie 8. (0-1) crrm? Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. (x2—3x)(x2+1) x2—25 A. jedno rozwiązanie. Równanie = (0 wzbiorze liczb rzeczywistych ma dokładnie B. dwa rozwiązania. C. trzy rozwiązania. D. cztery rozwiązania.

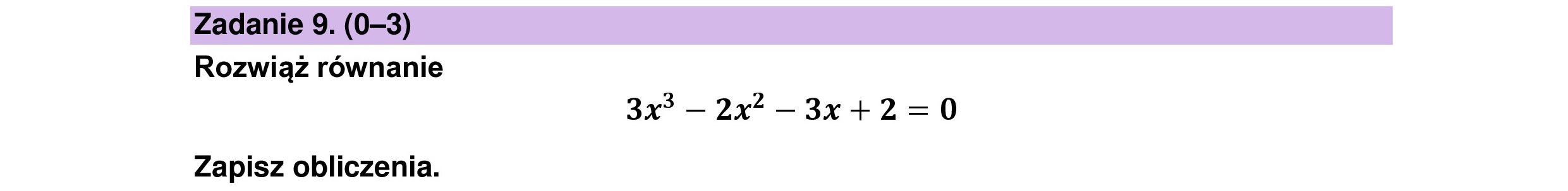
Zadanie 9. (0—3) Rozwiąż równanie 3x — 2x” —3x+2=0 Zapisz obliczenia.


Zadanie 10. (0-1) err Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. W kartezjańskim układzie współrzędnych (x,y), punkt (—8,6) jest punktem przecięcia prostych o równaniach A. 2x+3y=2 | —x ty = —14. B. 3x +2y = —12 i 2x +y=10. C. x+ty=-2 | x —2Ży=4. D. xy =—14 | —2x +y=22.


Zadanie 11. (0-1) err Miejscem zerowym funkcji liniowej f jest liczba 1. Wykres tej funkcji przechodzi przez punkt (—1, 4). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wzór funkcji f ma postać b 3 C. f(x) = —2x +2 D. f(x) = —3x +1 A. f(X) =-zx+1 B. f(X) = -3x+


Zadanie 12. (0-1) prrni Funkcja f_ jest określona dla każdej liczby rzeczywistej x wzorem f(x) = Żar » gdzie k jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek f(1) = 2. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wartość współczynnika k we wzorze tej funkcji jest równa A. (—3) B. 3 c. (—4) D. 4


Zadanie 13. (0-1) crrm* Funkcja kwadratowa f jest określona wzorem f(x) = (x — 13)? — 256. Jednym z miejsc zerowych tej funkcji jest liczba (—3). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Drugim miejscem zerowym funkcji f jest liczba A. (—29) B. (—23) C. 23 D. 29


Zadanie 14. W kartezjańskim układzie współrzędnych (x,y) narysowano wykres funkcji y = f(x) (zobacz rysunek). y Zadanie 14.1. (0-1)crrm7 Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Funkcja f jest rosnąca w przedziale A. [-5,4] B. [5,7] c. [1,5] D. [—1,5] Zadanie 14.2. (0—1) Zapisz poniżej w postaci sumy przedziałów zbiór wszystkich argumentów, dla których funkcja f przyjmuje wartości większe od 1. Zadanie 14.3. (0-1)crrm* Funkcja g jest określona za pomocą funkcji f następująco: g(x) = f(—x) dla każdego x € [—7,-5] U [—4,4] U [5,7]. Na jednym z rysunków A-D przedstawiono, w kartezjańskim układzie współrzędnych (x, y), wykres funkcji y = g(x). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wykres funkcji y = g(x) przedstawiono na rysunku A. y E. y | 6 SZSZSZ || 16 3 3 1 1 —7-6-5-4/3-—2-1, | 12 3 4567 x 77-6-5-935-2-1,| 12 3 67 x 15 [12 15 |—5


Zadanie 15. (0—2) Funkcje A,B,C, D,E oraz F są określone dla każdej liczby rzeczywistej x. Wzory tych funkcji podano poniżej. Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A-F i wpisz te litery w wykropkowanych miejscach. Przedział (—oo, 2] jest zbiorem wartości funkcji ............. EFEZ mamus s A. A(x) = —(x — 3)7 +2 D. D(x) = (x — 2)? B. B(x)=1x* +2 E. E(x) = 2x? —8x + 10 c. C(x) =—5(x — 2)? F. F(x) =—2x? + 4x


Zadanie 16. (0-1) prrni Ciąg (a,„) jest określony wzorem a, = (—1)”: m dla każdej liczby naturalnej n > 1. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Trzeci wyraz tego ciągu jest równy A. 2 B. (-2) c. 3 D. (—1)


Zadanie 17. (0-1) err Dany jest ciąg geometryczny (a,), określony dla każdej liczby naturalnej n > 1. Pierwszy wyraz tego ciągu jest równy 128, natomiast iloraz ciągu jest równy (-;). Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F — jeśli jest fałszywe. Wyraz 4023 jest liczbą ujemną. P F Różnica a3 — A jest równa 96.


Zadanie 18. (0—2) Ciąg (3x? + 5x, x?, 20 — x?) jest arytmetyczny. Oblicz x. Zapisz obliczenia.


Zadanie 19. (0-1) crrmó Kąt a jestostryi cosa = z, Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Sinus kąta a jest równy A. Es B. 25 /6 49 7 |e2 49 D. JI OT


Zadanie 20. (0-1) crrmó Trapez T, , o polurównym 52 iobwodzie 36, jest podobny do trapezu T;, . Pole trapezu T, jestrówne 13. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Obwód trapezu T> jest równy A. 18 B. 9 c. | D. Sa


Zadanie 21. (0-1) crrm* Koło ma promień równy 3. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Obwód wycinka tego koła o kącie środkowym 30” jest równy 3 1 A. 47 B. 7" G. LEK D. 51 +6


Zadanie 22. (0-1) rrrm4 W okręgu O kątśrodkowy E oraz kąt wpisany a są oparte na tym samym łuku. Kąt 8 ma miarę o 40” większą od kąta a. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Miara kąta 5 jest równa A. 40? B. 80? c. 100” D. 120?


Zadanie 23. (0-1) zrm W trójkącie ABC długość boku AC jestrówna 3, a długość boku BC jest równa 4. Dwusieczna kąta ACB przecina bok AB w punkcie D. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Stosunek |AD| : |DB| jest równy A. 4:3 B. 4:7 C. 3:4 D. 3:7


Zadanie 24. (0—2) Dany jest trapez równoramienny ABCD, w którym podstawa CD ma długość 6, ramię AD ma długość 4, akąty BAD oraz ABC mają miarę 60” (zobacz rysunek). D 6 C 4 A (a A B Oblicz pole tego trapezu. Zapisz obliczenia.


Zadanie 25. (0-1) crrm4 W kartezjańskim układzie współrzędnych (x,y) dane są prosta k o równaniu y = qx -3 oraz punkt P = (12, —1). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Prosta przechodząca przez punkt Pi równoległa do prostej k ma równanie A.y=—qx+8 B. y= qx—10 C.y= 3x —17 D.y=-gx+15 4


Zadanie 26. (0-1) crrm* W kartezjańskim układzie współrzędnych (x,y) dany jest okrąg O o środku S = (—1,2) i promieniu 3. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Okrąg O jest określony równaniem A. (x—1)?+(y +2)? =9 B. (x—1)7+(y+2)7=3 C. (x +1)” +(y-2)7=9 D. (x+1)7+(y-2)7=3


Zadanie 27. (0-1) crrm” W kartezjańskim układzie współrzędnych (x,y) proste o równaniach: 1 . = 3x +6 e = —43x + 6 . =——x— y y y J3% Ży przecinają się w punktach, które są wierzchołkami trójkąta KLM. Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3. Trójkąt KLM jest oś Ox przechodzi przez jeden z wierzchołków 1. | tego trójkąta i środek jednego z boków tego A. | równoramienny, trójkąta ponieważ | 2. | dwie z tych prostych są prostopadłe. B. | prostokątny, 3. |oś Oy zawiera dwusieczną tego trójkąta.


Zadanie 28. (0-1) err W kartezjańskim układzie współrzędnych (x,y) punkt A = (—1, —4) jest wierzchołkiem równoległoboku ABCD. Punkt S = (2,2) jest środkiem symetrii tego równoległoboku. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Długość przekątnej AC równoległoboku ABCD jest równa A. V5 B. 2Y5 Cc. 3Y5 D. 6Y5


Zadanie 29. Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Zadanie 29.1. (0-1)rrrm* Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Pole powierzchni całkowitej tego graniastosłupa jest równe A. 216 + 18V3 B. 216 + 54V3 C. 216 + 216V3 D. 216 + 108V3 Zadanie 29.2. (0—1) Oblicz cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa. Zapisz obliczenia.


Zadanie 30. (0-1) rrr Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wszystkich liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym cyfry się nie powtarzają, jest A. 9:10:10:10:10 B. 9-9-9-9 C. 10:9:8:7 D. 9:9:8:7


Zadanie 31. (0-2) Ze zbioru pięciu liczb f1, 2, 3,4,5) losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że obie wylosowane liczby są nieparzyste. Zapisz obliczenia.


Zadanie 32. (0-1) crrm* Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich stu pracowników pewnej firmy za styczeń 2023 roku. 30 36 35 30 liczba 25 pracowników 20 15 10 5 2 0 25 18 10 4800 5100 5500 5900 6400 7500 8600 wynagrodzenie brutto za styczeń 2023 (w zł) Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Średnia wynagrodzenia brutto wszystkich pracowników tej firmy za styczeń 2023 roku jest równa A. 5690 zł B. 5 280 zł C. 6257 zł D. 5900 zł


Zadanie 33. (0-4) Zakład stolarski produkuje krzesła, które sprzedaje po 196 złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że: e przychód P (w złotych) ze sprzedaży x krzeseł można opisać funkcją P(x) = 196x e koszt K (w złotych) produkcji x krzeseł dziennie można opisać funkcją K(x) = 4x? + 4x + 240 Dziennie w zakładzie można wyprodukować co najwyżej 30 krzeseł. Oblicz, ile krzeseł powinien dziennie sprzedawać zakład, aby zysk ze sprzedaży krzeseł wyprodukowanych przez ten zakład w ciągu jednego dnia był możliwie największy. Oblicz ten największy zysk. Zapisz obliczenia. Wskazówka: przyjmij, że zysk jest różnicą przychodu i kosztów.






























