MATEMATYKA 2023 MAJ MATURA STARA PODSTAWOWA

Zadanie 1. (0—1) Liczba logo 27 + logg 3 jest równa A. 81 B. 9


Zadanie 2. (0—1) Liczba |-q6' V2 jest równa A. (- ;) B. 3 WIN


Zadanie 3. (0-1) Cenę aparatu fotograficznego obniżono o 15%, a następnie o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po tych dwóch obniżkach aparat kosztuje 340 zł. Przed obiema obniżkami cena tego aparatu była równa A. 500zł B. 425zł Cc. 400zł D. 375zł


Zadanie 4. (0—1) Dla każdej liczby rzeczywistej a wyrażenie (2a — 3)? — (2a + 3)? jest równe A. —24a B. 0 Cc. 18 D. 16a? — 24a

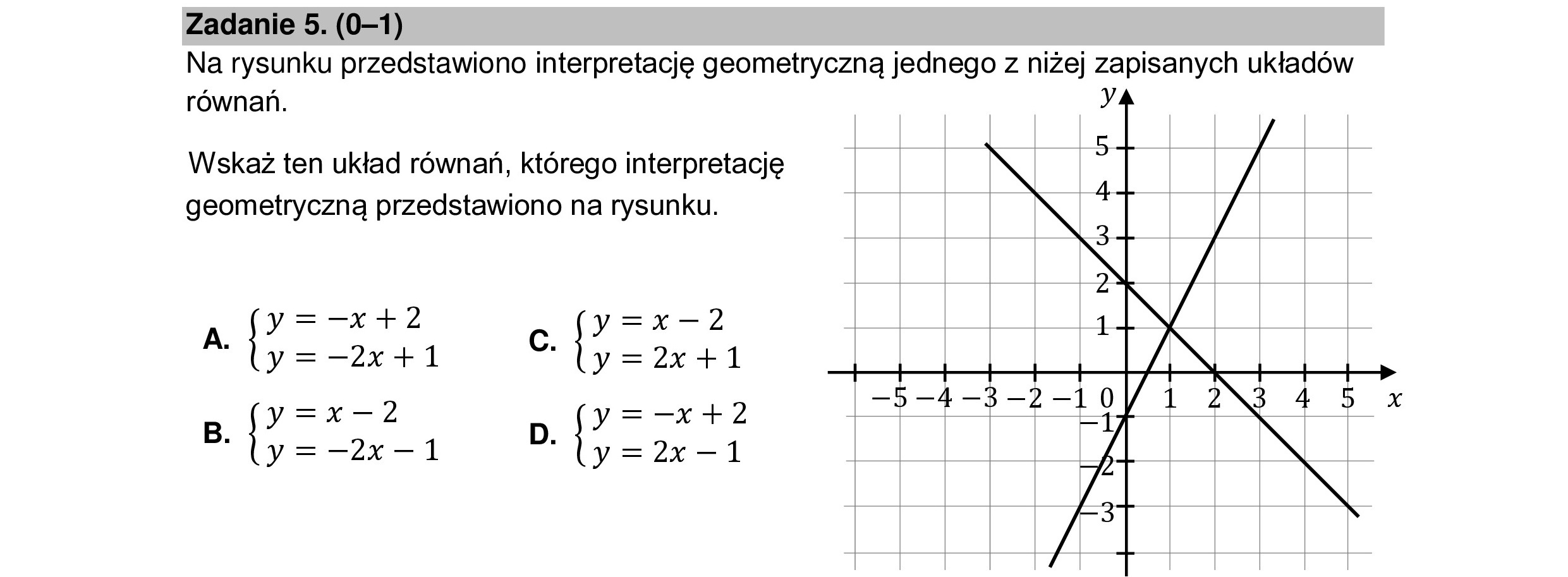
Zadanie 5. (0—1) Na rysunku przedstawiono interpretację geometryczną jednego z niżej zapisanych układów równań. Wskaż ten układ równań, którego interpretację geometryczną przedstawiono na rysunku. A IE y=w—2 "ly=-2x+1 mig = Zede1 y=m—2 Y=—x+2 a |v=-2x-1 D. by=2e-1

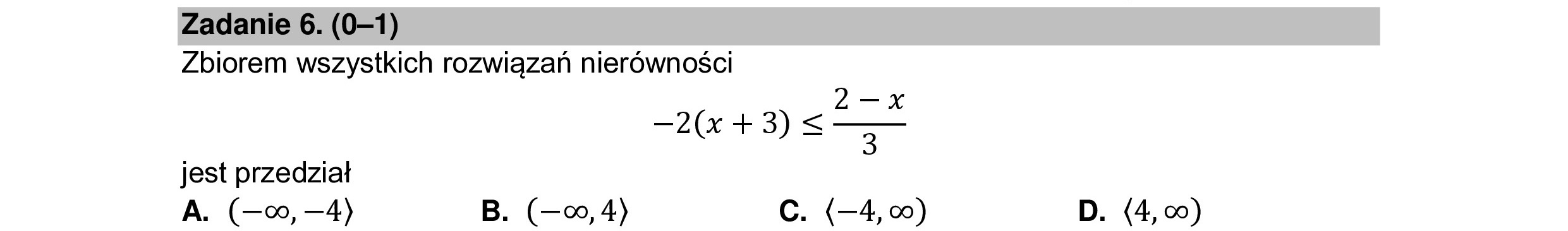
Zadanie 6. (0—1) Zbiorem wszystkich rozwiązań nierówności 2=X —2(x + 3) < 3 jest przedział A. (—o, —4) B. (—%,4) C. (—4,0) D. (4,00)

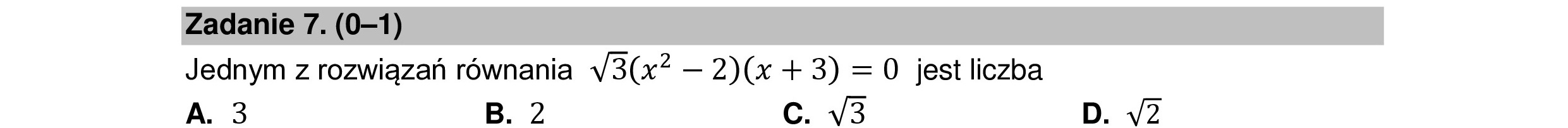
Zadanie 7. (0—1) Jednym z rozwiązań równania V3(x? — 2)(x + 3) =0 jest liczba A. 3 B. 2 G. :/3 D. vŻ


Zadanie 8. (0—1) (c+1)(x—1)? (x-1)(x+1) A. nie ma rozwiązania. Równanie = (0 wzbiorze liczb rzeczywistych B. ma dokładnie jedno rozwiązanie: —1. C. ma dokładnie jedno rozwiązanie: 1. D. ma dokładnie dwa rozwiązania: —1 oraz 1.

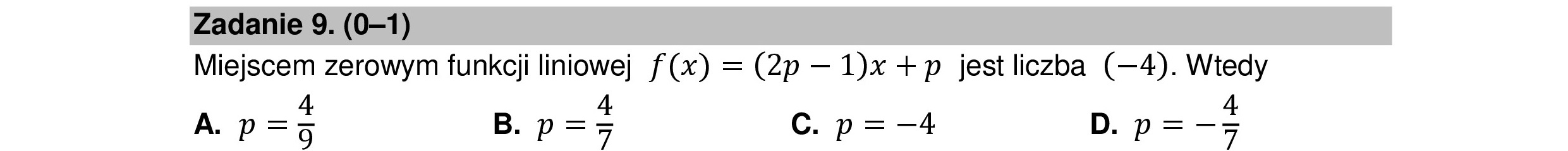
Zadanie 9. (0—1) Miejscem zerowym funkcji liniowej f(x) = (2p — 1)x +p jest liczba (—4). Wtedy 4 4 4 A.p=g B.p=> C. p=—4 D.p=->


Zadanie 10. (0—1) Funkcja liniowa f jest określona wzorem f(x) =ax +b,gdzie a i b są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji f w układzie współrzędnych (x,y). Liczba a oraz liczba b we wzorze funkcji f spełniają warunki: A.a>0ib>0. B.a>0ib<0. C.a<0ib>0. D.a<0ib<0.

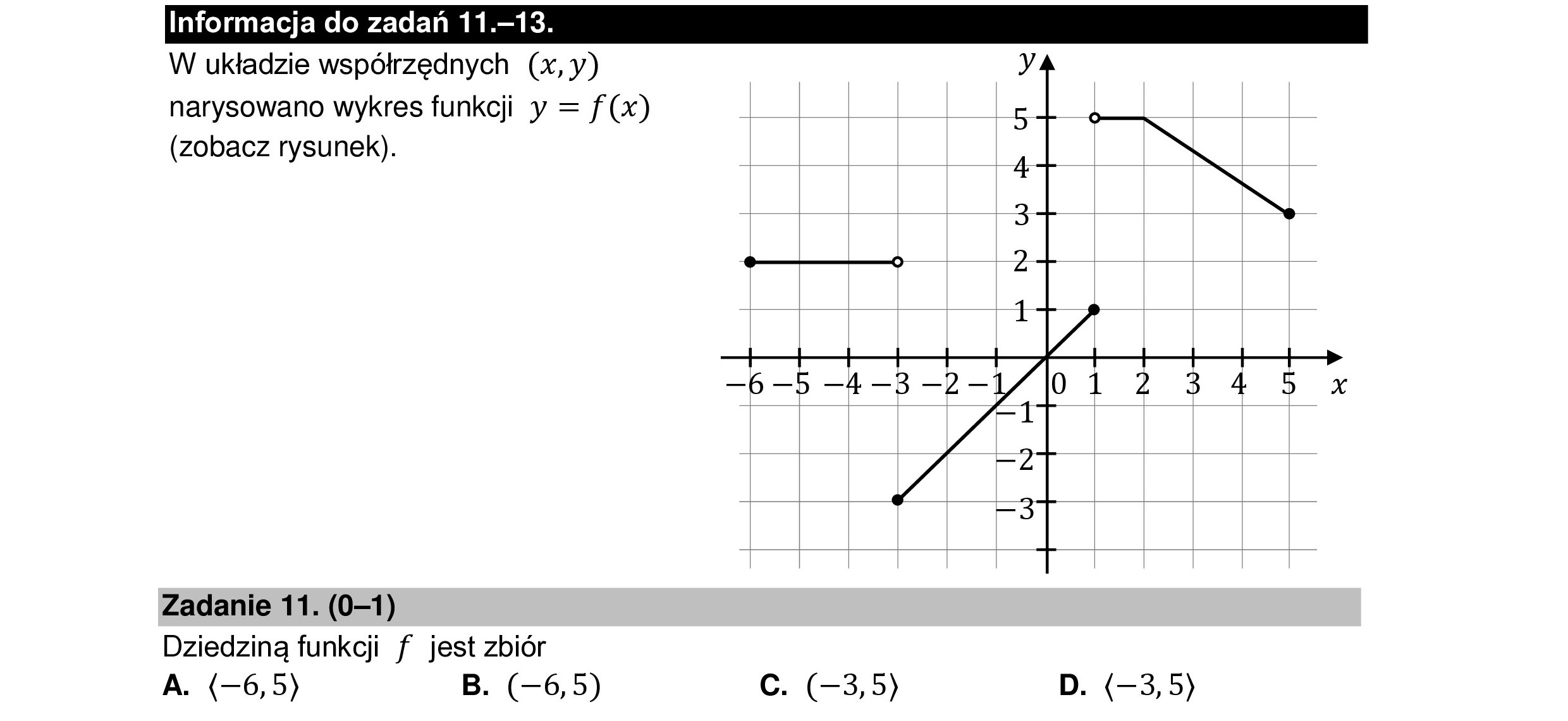
Informacja do zadań 11.—13. W układzie współrzędnych (x,y) narysowano wykres funkcji y = f(x) (zobacz rysunek). Zadanie 11. (0—1) Dziedziną funkcji f jest zbiór A. (—6,5) B. (—6,5) Ć. (—38,5) D. (—3,5)

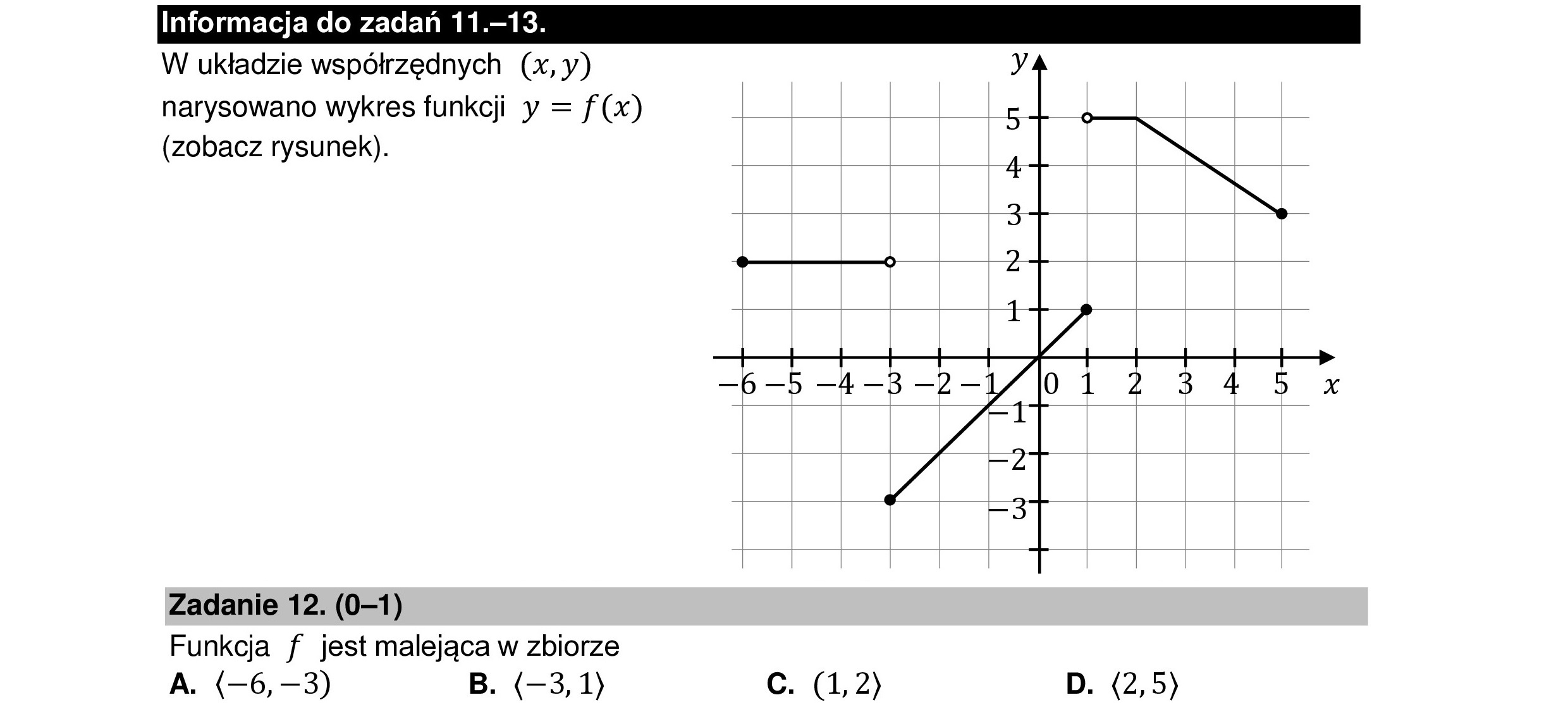
Informacja do zadań 11.—13. W układzie współrzędnych (x,y) narysowano wykres funkcji y = f(x) (zobacz rysunek). Zadanie 12. (0—1) Funkcja f jest malejąca w zbiorze A. (—6, —3) B. (—3,1) c. (1,2) D. (2,5)

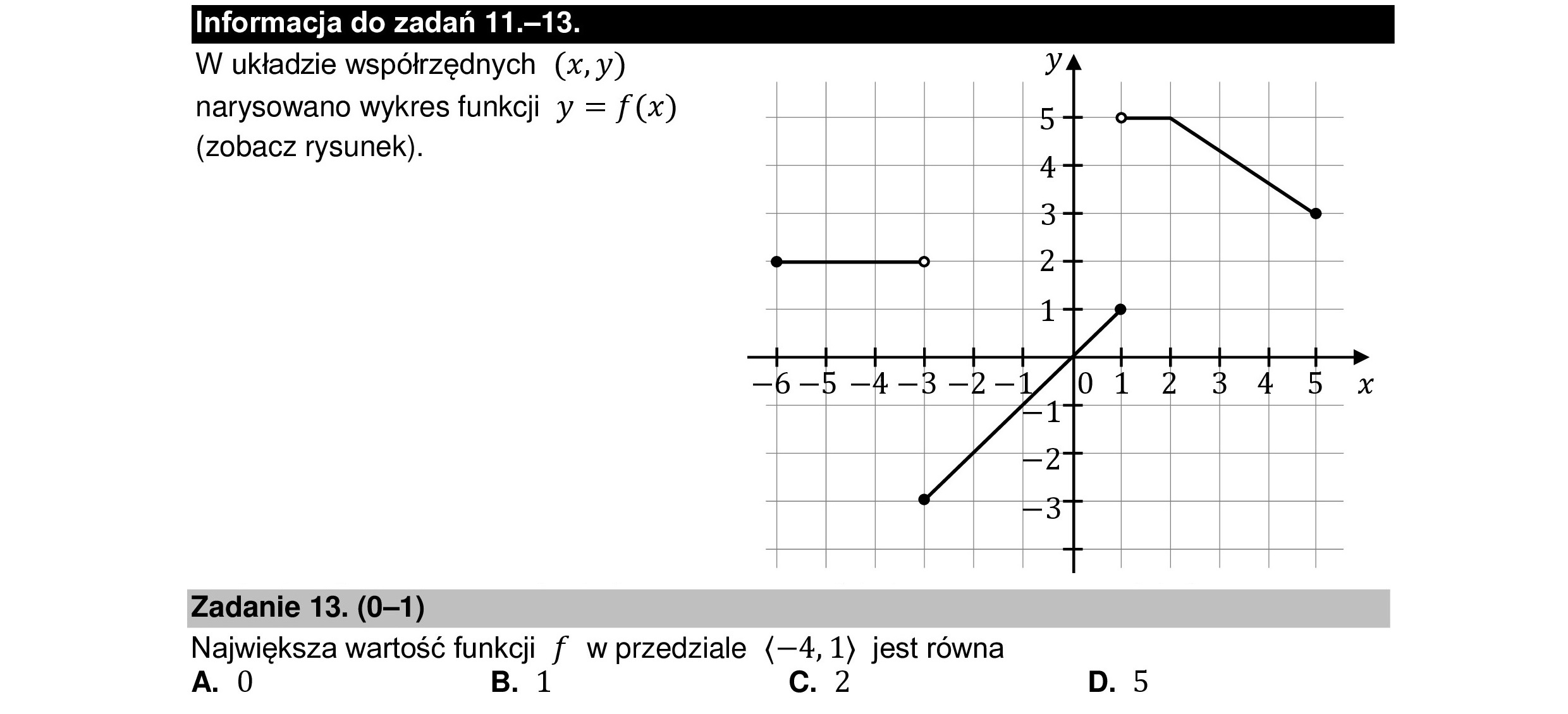
Informacja do zadań 11.—13. W układzie współrzędnych (x,y) narysowano wykres funkcji y = f(x) (zobacz rysunek). Zadanie 13. (0—1) Największa wartość funkcji f w przedziale (—4, 1) jest równa A. 0 B. 1 c. 2


Zadanie 14. (0—1) Jednym z miejsc zerowych funkcji kwadratowej f jest liczba (—5). Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji f, jest równa 3. Drugim miejscem zerowym funkcji f jest liczba A. 11 B. 1 c. (—1) D. (—13)

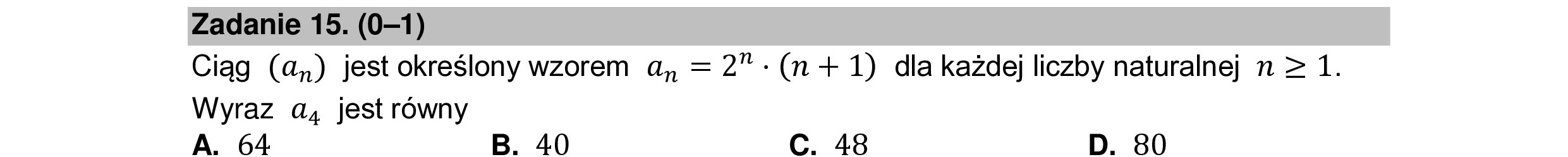
Zadanie 15. (0—1) Ciąg (a,„) jest określony wzorem a, =2”:(n+ 1) dla każdej liczby naturalnej n > 1. Wyraz a, jest równy A. 64 B. 40 C. 48 D. 80


Zadanie 16. (0—1) Trzywyrazowy ciąg (27, 9, a— 1) jest geometryczny. Liczba a jest równa A 3 B. 0 C. 4

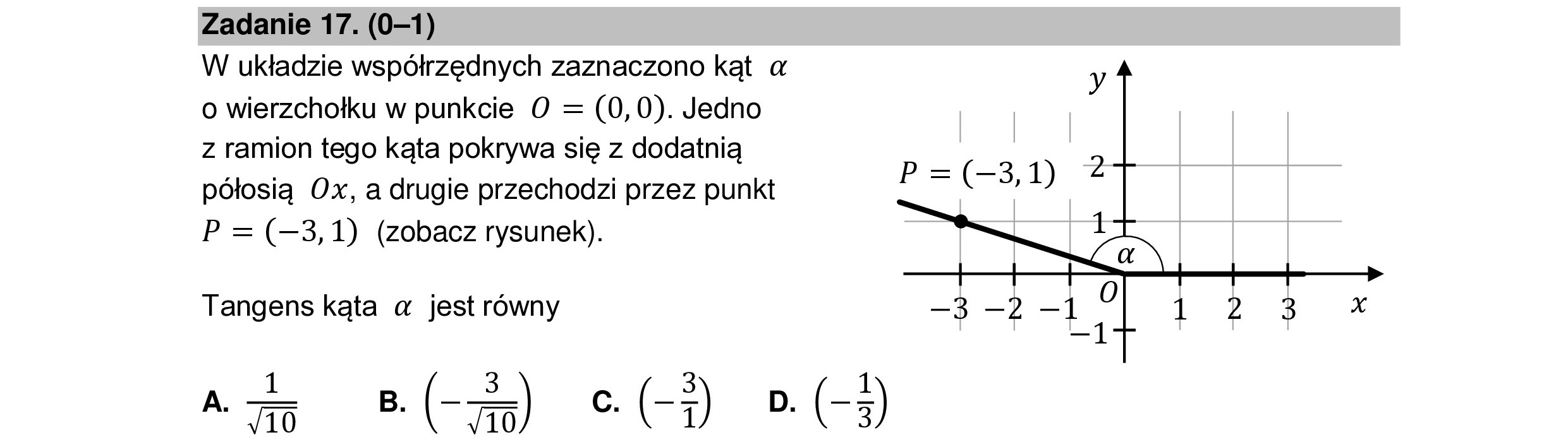
Zadanie 17. (0—1) W układzie współrzędnych zaznaczono kąt a o wierzchołku w punkcie O = (0,0). Jedno z ramion tego kąta pokrywa się z dodatnią półosią Ox, a drugie przechodzi przez punkt P = (—3,1) (zobacz rysunek). Tangens kąta a jest równy A. 5 B. (-75) c. (-7) D. (-3)

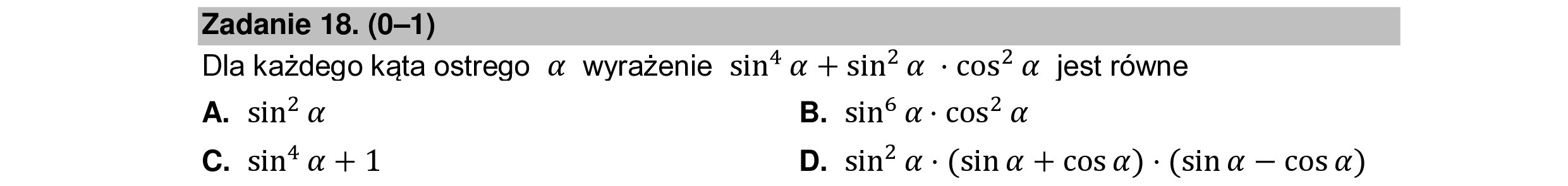
Zadanie 18. (0—1) Dla każdego kąta ostrego a wyrażenie sin* a + sin? a : cos? a jest równe A. sin? a B. sin a: cos?” a C. sin” a + 1 D. sin? a : (sina + cosa) : (sina — cosa)

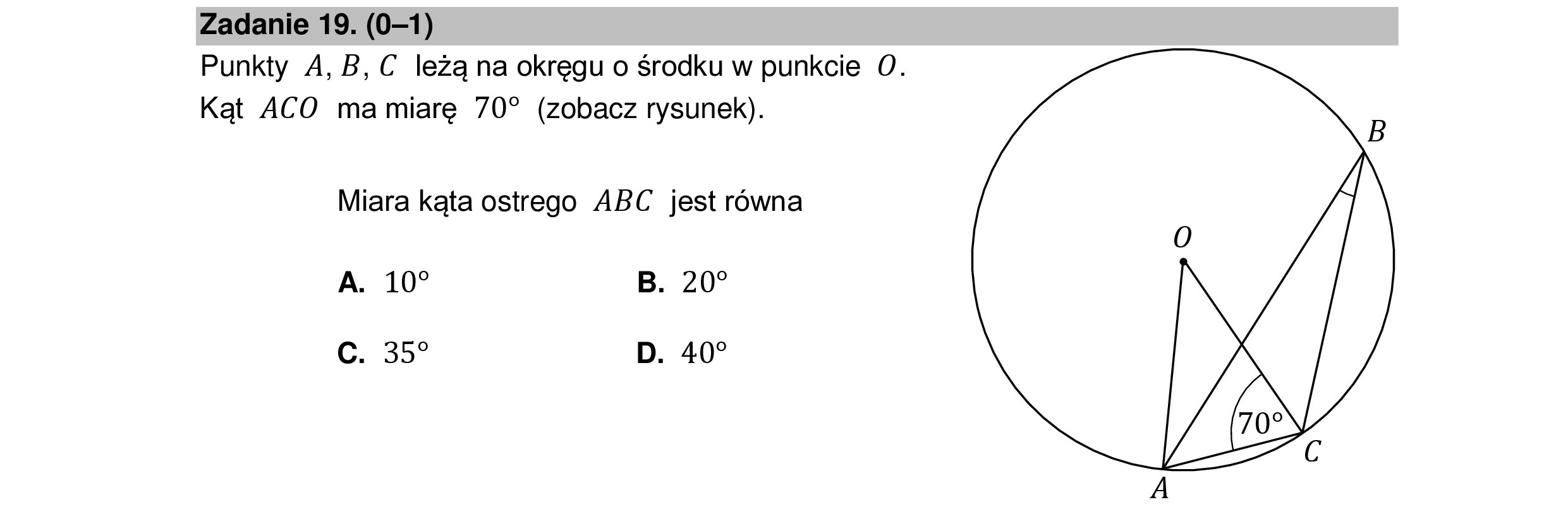
Zadanie 19. (0—1) Punkty 4, B,C leżą na okręgu o środku w punkcie O. Kąt ACO ma miarę 70? (zobacz rysunek). Miara kąta ostrego ABC jest równa A. 10? B. 20? c. 359 D. 40?


Zadanie 20. (0—1) W rombie o boku długości 6V2 kąt rozwarty ma miarę 1507. Iloczyn długości przekątnych tego rombu jest równy A. 24 B. 72 Cc. 36 D. 36V2

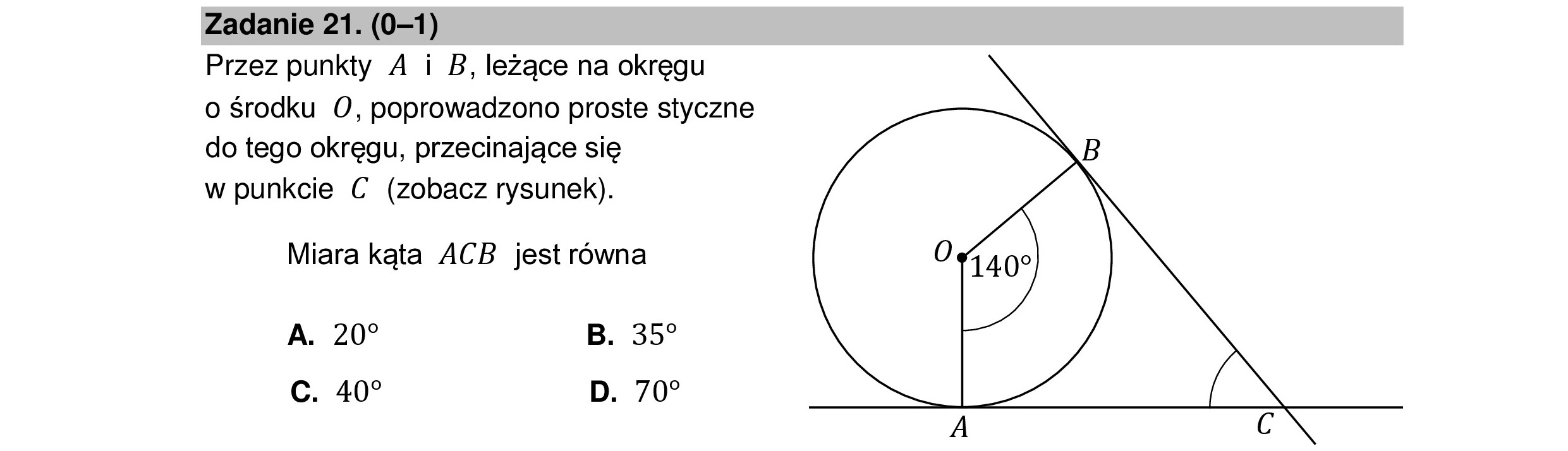
Zadanie 21. (0—1) Przez punkty A i B, leżące na okręgu o środku O, poprowadzono proste styczne do tego okręgu, przecinające się B w punkcie C (zobacz rysunek). Miara kąta ACB jest równa A. 20? B. 357 C. 400 D. 702 AN

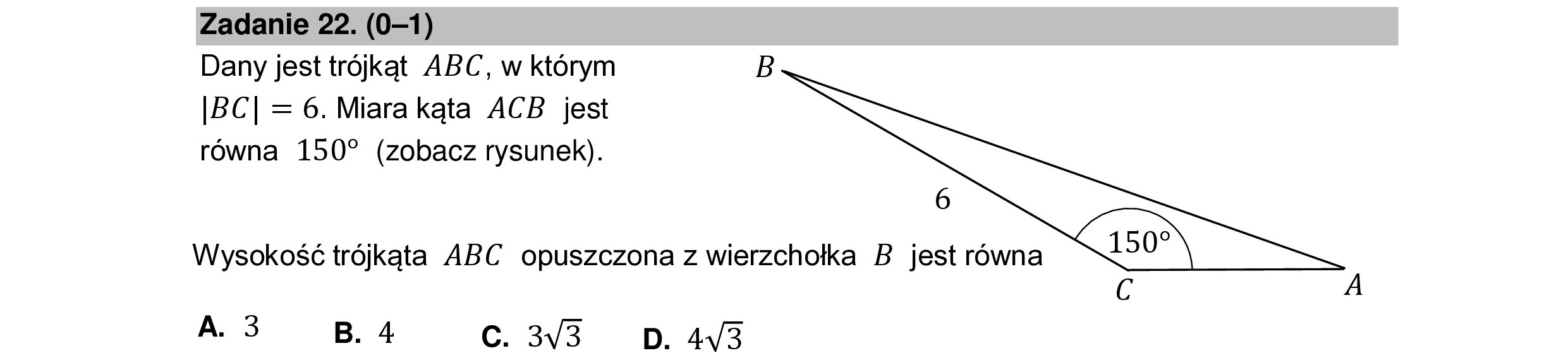
Zadanie 22. (0—1) Dany jest trójkąt ABC, w którym B |BC| = 6. Miara kąta ACB jest równa 150? (zobacz rysunek). Wysokość trójkąta ABC opuszczona z wierzchołka B jest równa A. 3 B. 4 C. 3V3 D. 44/3


Zadanie 23. (0—1) Dana jest prosta k o równaniu y = gz + 2. Prosta o równaniu y = ax + b jest równoległa do prostej k i przechodzi przez punkt P = (3,5), gdy A.a=3ib=4. B.a=-3ib=4. C.a=3ib=—4. D.a=-zib=6.


Zadanie 24. (0—1) Dane są punkty K = (—3,—7) oraz S = (5,3). Punkt S jest środkiem odcinka KL. Wtedy punkt L ma współrzędne A. (13,10) B. (13,13) Cc. (1 —2) D. (7, —1)


Zadanie 25. (0—1) Dana jest prosta o równaniu y = 2x — 3. Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu A. y=2x+3 B. y= —2x—3 C. y=-2x+3 D.y=2x-—3


Zadanie 26. (0—1) Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem a takim, że cosa = z, Długość przekątnej tego graniastosłupa jest równa A. 15V2 B. 45 c. 5v2 D. 10


Zadanie 27. (0-1) Średnia arytmetyczna liczb x, y, z jest równa 4. Średnia arytmetyczna czterech liczb: 1 + x, 2 +y, 3 + z, 14, jest równa A. 6 B. 9 c. 8 D. 13


Zadanie 28. (0—1) Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry 0,5, 7 (np. 57 075, 55 555), jest A. 5 B. 2-43 c. 2:3* D. 3?


Zadanie 29. (0—1) W pewnym ostrosłupie prawidłowym stosunek liczby W. wszystkich wierzchołków do liczby K wszystkich krawędzi jest równy ud = :. Podstawą tego ostrosłupa jest A. kwadrat. B. pięciokąt foremny. C. sześciokąt foremny. D. siedmiokąt foremny.

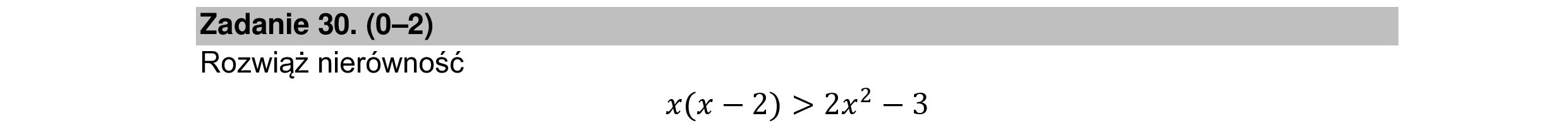
Rozwiąż nierówność x(x — 2) > 2x* —3


Zadanie 31. (0—2) Pan Stanisław spłacił pożyczkę w wysokości 8910 zł w osiemnastu ratach. Każda kolejna rata była mniejsza od poprzedniej o 30 zł. Oblicz kwotę pierwszej raty.

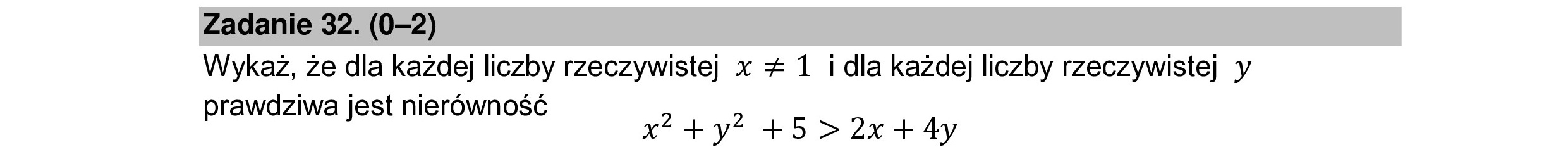
Zadanie 32. (0-2) Wykaż, że dla każdej liczby rzeczywistej x ź 1 i dla każdej liczby rzeczywistej y prawdziwa jest nierówność p z x*+y” +5>2x+4y


Zadanie 33. (0—2) Trójkąty prostokątne T; i Tą są podobne. Przyprostokątne trójkąta T;, mają długości 5 i 12. Przeciwprostokątna trójkąta Tę ma długość 26. Oblicz pole trójkąta T3.


Zadanie 34. (0—2) W kwadracie ABCD punkty A = (—8, —2) oraz € = (0,4) są końcami przekątnej. Wyznacz równanie prostej zawierającej przekątną BD tego kwadratu.


Zadanie 35. (0-2) Ze zbioru ośmiu liczb (2, 3, 4,5, 6, 7,8,9) losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 15.

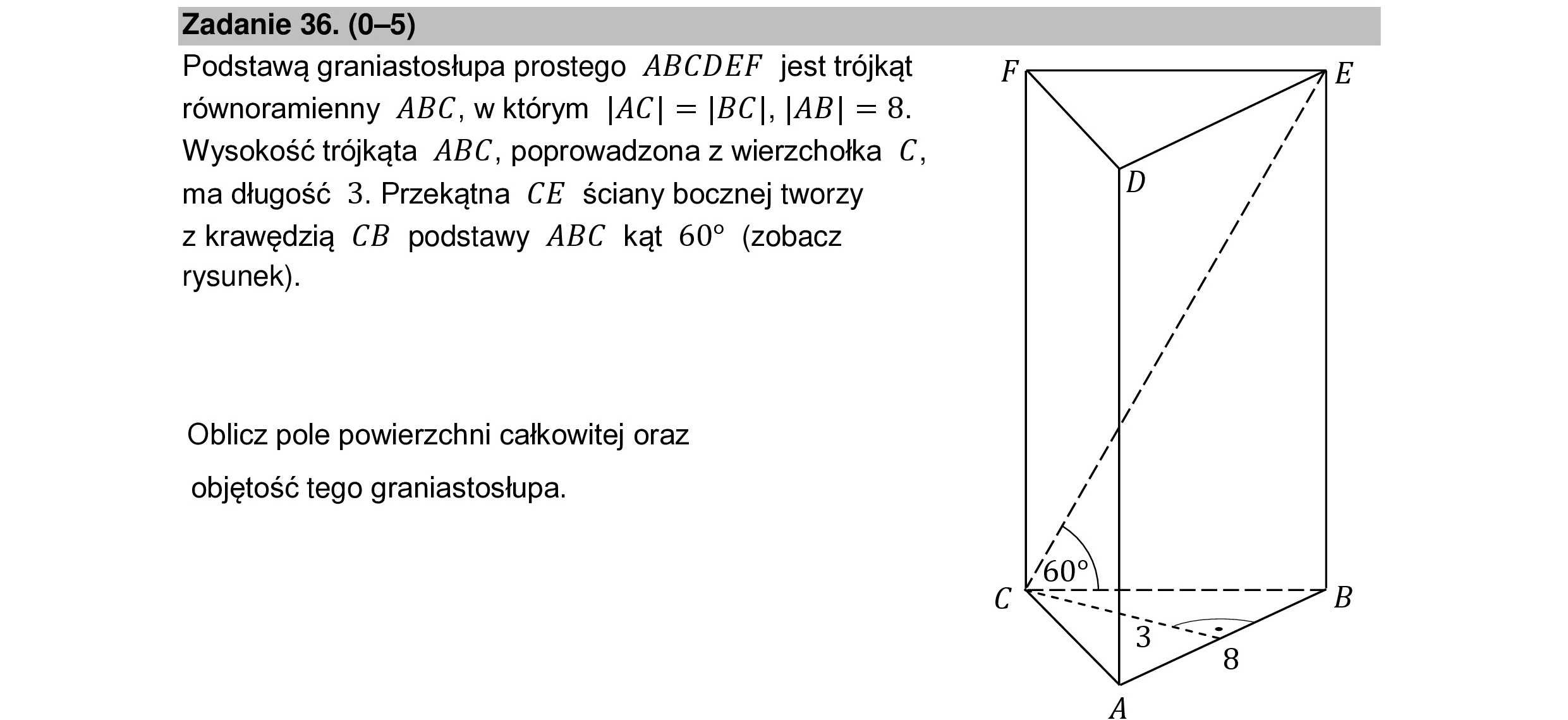
Zadanie 36. (0-5) Podstawą graniastosłupa prostego ABCDEF jest trójkąt równoramienny ABC, w którym |AC| = |BC|, |AB| =8. Wysokość trójkąta ABC, poprowadzona z wierzchołka C, ma długość 3. Przekątna CE ściany bocznej tworzy z krawędzią CB podstawy ABC kąt 60” (zobacz rysunek). Oblicz pole powierzchni całkowitej oraz objętość tego graniastosłupa.

MATEMATYKA 2023 MAJ MATURA STARA PODSTAWOWA

Zadanie 1. (0—1) Liczba logo 27 + logg 3 jest równa A. 81 B. 9


Zadanie 2. (0—1) Liczba |-q6' V2 jest równa A. (- ;) B. 3 WIN


Zadanie 3. (0-1) Cenę aparatu fotograficznego obniżono o 15%, a następnie o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po tych dwóch obniżkach aparat kosztuje 340 zł. Przed obiema obniżkami cena tego aparatu była równa A. 500zł B. 425zł Cc. 400zł D. 375zł


Zadanie 4. (0—1) Dla każdej liczby rzeczywistej a wyrażenie (2a — 3)? — (2a + 3)? jest równe A. —24a B. 0 Cc. 18 D. 16a? — 24a


Zadanie 5. (0—1) Na rysunku przedstawiono interpretację geometryczną jednego z niżej zapisanych układów równań. Wskaż ten układ równań, którego interpretację geometryczną przedstawiono na rysunku. A IE y=w—2 "ly=-2x+1 mig = Zede1 y=m—2 Y=—x+2 a |v=-2x-1 D. by=2e-1

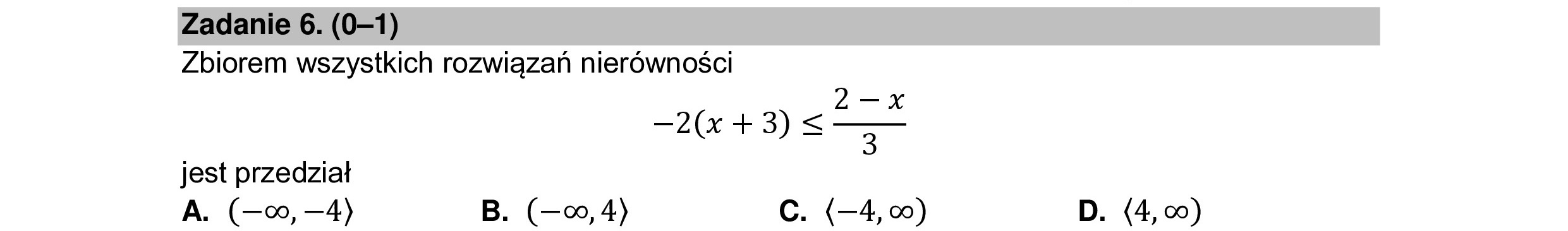
Zadanie 6. (0—1) Zbiorem wszystkich rozwiązań nierówności 2=X —2(x + 3) < 3 jest przedział A. (—o, —4) B. (—%,4) C. (—4,0) D. (4,00)

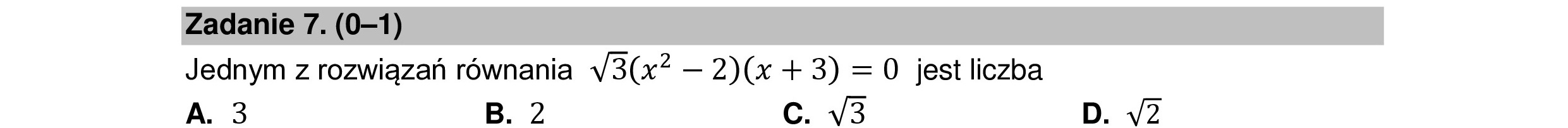
Zadanie 7. (0—1) Jednym z rozwiązań równania V3(x? — 2)(x + 3) =0 jest liczba A. 3 B. 2 G. :/3 D. vŻ


Zadanie 8. (0—1) (c+1)(x—1)? (x-1)(x+1) A. nie ma rozwiązania. Równanie = (0 wzbiorze liczb rzeczywistych B. ma dokładnie jedno rozwiązanie: —1. C. ma dokładnie jedno rozwiązanie: 1. D. ma dokładnie dwa rozwiązania: —1 oraz 1.

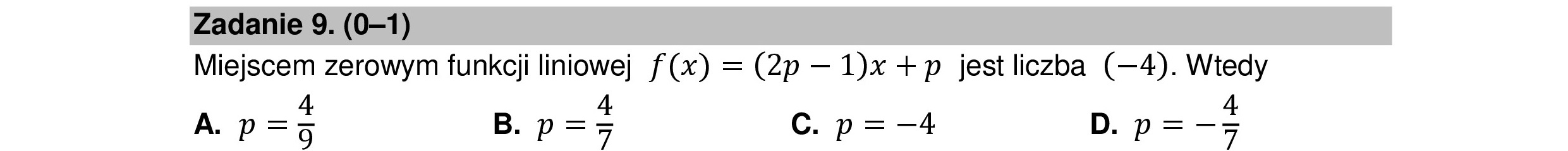
Zadanie 9. (0—1) Miejscem zerowym funkcji liniowej f(x) = (2p — 1)x +p jest liczba (—4). Wtedy 4 4 4 A.p=g B.p=> C. p=—4 D.p=->


Zadanie 10. (0—1) Funkcja liniowa f jest określona wzorem f(x) =ax +b,gdzie a i b są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji f w układzie współrzędnych (x,y). Liczba a oraz liczba b we wzorze funkcji f spełniają warunki: A.a>0ib>0. B.a>0ib<0. C.a<0ib>0. D.a<0ib<0.


Informacja do zadań 11.—13. W układzie współrzędnych (x,y) narysowano wykres funkcji y = f(x) (zobacz rysunek). Zadanie 11. (0—1) Dziedziną funkcji f jest zbiór A. (—6,5) B. (—6,5) Ć. (—38,5) D. (—3,5)


Informacja do zadań 11.—13. W układzie współrzędnych (x,y) narysowano wykres funkcji y = f(x) (zobacz rysunek). Zadanie 12. (0—1) Funkcja f jest malejąca w zbiorze A. (—6, —3) B. (—3,1) c. (1,2) D. (2,5)


Informacja do zadań 11.—13. W układzie współrzędnych (x,y) narysowano wykres funkcji y = f(x) (zobacz rysunek). Zadanie 13. (0—1) Największa wartość funkcji f w przedziale (—4, 1) jest równa A. 0 B. 1 c. 2


Zadanie 14. (0—1) Jednym z miejsc zerowych funkcji kwadratowej f jest liczba (—5). Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji f, jest równa 3. Drugim miejscem zerowym funkcji f jest liczba A. 11 B. 1 c. (—1) D. (—13)

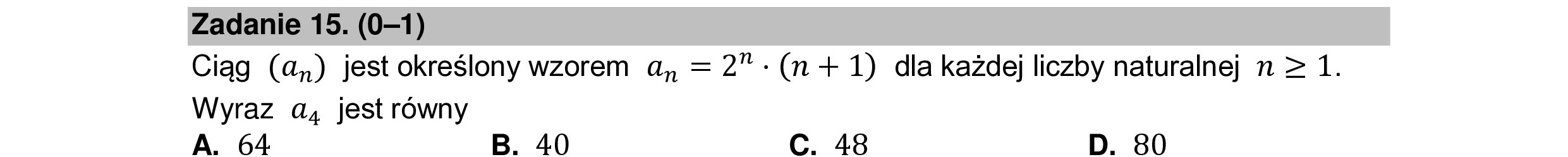
Zadanie 15. (0—1) Ciąg (a,„) jest określony wzorem a, =2”:(n+ 1) dla każdej liczby naturalnej n > 1. Wyraz a, jest równy A. 64 B. 40 C. 48 D. 80


Zadanie 16. (0—1) Trzywyrazowy ciąg (27, 9, a— 1) jest geometryczny. Liczba a jest równa A 3 B. 0 C. 4


Zadanie 17. (0—1) W układzie współrzędnych zaznaczono kąt a o wierzchołku w punkcie O = (0,0). Jedno z ramion tego kąta pokrywa się z dodatnią półosią Ox, a drugie przechodzi przez punkt P = (—3,1) (zobacz rysunek). Tangens kąta a jest równy A. 5 B. (-75) c. (-7) D. (-3)

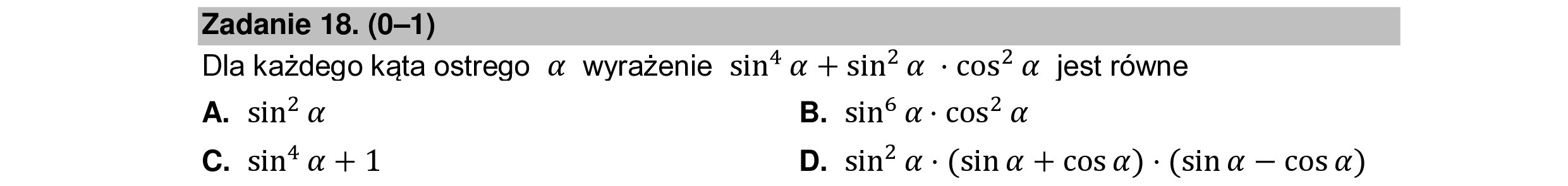
Zadanie 18. (0—1) Dla każdego kąta ostrego a wyrażenie sin* a + sin? a : cos? a jest równe A. sin? a B. sin a: cos?” a C. sin” a + 1 D. sin? a : (sina + cosa) : (sina — cosa)


Zadanie 19. (0—1) Punkty 4, B,C leżą na okręgu o środku w punkcie O. Kąt ACO ma miarę 70? (zobacz rysunek). Miara kąta ostrego ABC jest równa A. 10? B. 20? c. 359 D. 40?


Zadanie 20. (0—1) W rombie o boku długości 6V2 kąt rozwarty ma miarę 1507. Iloczyn długości przekątnych tego rombu jest równy A. 24 B. 72 Cc. 36 D. 36V2


Zadanie 21. (0—1) Przez punkty A i B, leżące na okręgu o środku O, poprowadzono proste styczne do tego okręgu, przecinające się B w punkcie C (zobacz rysunek). Miara kąta ACB jest równa A. 20? B. 357 C. 400 D. 702 AN


Zadanie 22. (0—1) Dany jest trójkąt ABC, w którym B |BC| = 6. Miara kąta ACB jest równa 150? (zobacz rysunek). Wysokość trójkąta ABC opuszczona z wierzchołka B jest równa A. 3 B. 4 C. 3V3 D. 44/3


Zadanie 23. (0—1) Dana jest prosta k o równaniu y = gz + 2. Prosta o równaniu y = ax + b jest równoległa do prostej k i przechodzi przez punkt P = (3,5), gdy A.a=3ib=4. B.a=-3ib=4. C.a=3ib=—4. D.a=-zib=6.


Zadanie 24. (0—1) Dane są punkty K = (—3,—7) oraz S = (5,3). Punkt S jest środkiem odcinka KL. Wtedy punkt L ma współrzędne A. (13,10) B. (13,13) Cc. (1 —2) D. (7, —1)


Zadanie 25. (0—1) Dana jest prosta o równaniu y = 2x — 3. Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu A. y=2x+3 B. y= —2x—3 C. y=-2x+3 D.y=2x-—3


Zadanie 26. (0—1) Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem a takim, że cosa = z, Długość przekątnej tego graniastosłupa jest równa A. 15V2 B. 45 c. 5v2 D. 10


Zadanie 27. (0-1) Średnia arytmetyczna liczb x, y, z jest równa 4. Średnia arytmetyczna czterech liczb: 1 + x, 2 +y, 3 + z, 14, jest równa A. 6 B. 9 c. 8 D. 13


Zadanie 28. (0—1) Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry 0,5, 7 (np. 57 075, 55 555), jest A. 5 B. 2-43 c. 2:3* D. 3?


Zadanie 29. (0—1) W pewnym ostrosłupie prawidłowym stosunek liczby W. wszystkich wierzchołków do liczby K wszystkich krawędzi jest równy ud = :. Podstawą tego ostrosłupa jest A. kwadrat. B. pięciokąt foremny. C. sześciokąt foremny. D. siedmiokąt foremny.

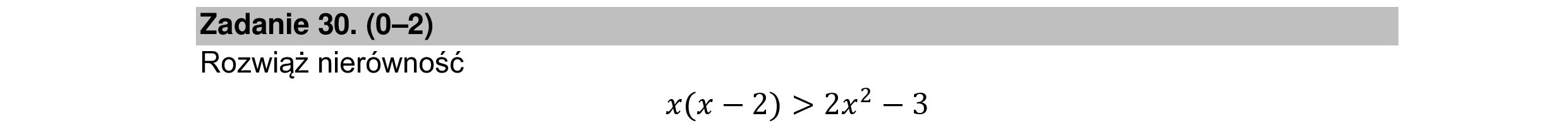
Rozwiąż nierówność x(x — 2) > 2x* —3


Zadanie 31. (0—2) Pan Stanisław spłacił pożyczkę w wysokości 8910 zł w osiemnastu ratach. Każda kolejna rata była mniejsza od poprzedniej o 30 zł. Oblicz kwotę pierwszej raty.

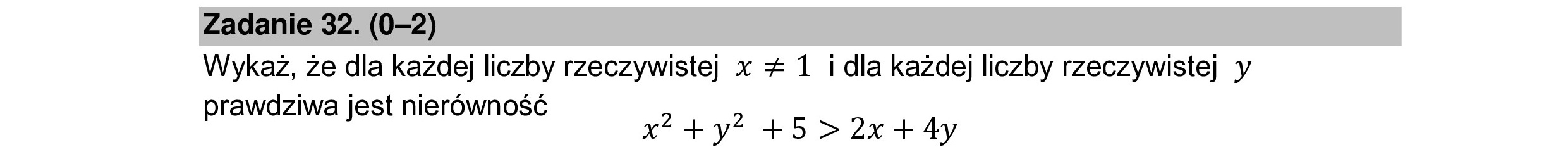
Zadanie 32. (0-2) Wykaż, że dla każdej liczby rzeczywistej x ź 1 i dla każdej liczby rzeczywistej y prawdziwa jest nierówność p z x*+y” +5>2x+4y


Zadanie 33. (0—2) Trójkąty prostokątne T; i Tą są podobne. Przyprostokątne trójkąta T;, mają długości 5 i 12. Przeciwprostokątna trójkąta Tę ma długość 26. Oblicz pole trójkąta T3.


Zadanie 34. (0—2) W kwadracie ABCD punkty A = (—8, —2) oraz € = (0,4) są końcami przekątnej. Wyznacz równanie prostej zawierającej przekątną BD tego kwadratu.


Zadanie 35. (0-2) Ze zbioru ośmiu liczb (2, 3, 4,5, 6, 7,8,9) losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 15.


Zadanie 36. (0-5) Podstawą graniastosłupa prostego ABCDEF jest trójkąt równoramienny ABC, w którym |AC| = |BC|, |AB| =8. Wysokość trójkąta ABC, poprowadzona z wierzchołka C, ma długość 3. Przekątna CE ściany bocznej tworzy z krawędzią CB podstawy ABC kąt 60” (zobacz rysunek). Oblicz pole powierzchni całkowitej oraz objętość tego graniastosłupa.






























