MATEMATYKA 2022 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) —40 Liczba PUJ jest równa A, 474 B. 4770 Cc. 2747 D. 27130


Zadanie 2. (0-1) Liczba log» 32 — loga 8 jest równa A. 2 B. 14 C. 16 D. 24


Zadanie 3. (0-1) Liczba (5 — 2Y3) jest równa A. 25 +43 B. 25 — 4/3 C. 37 + 20V3 D. 37 — 20V3


Zadanie 4. (0—1) Cenę x (w złotych) pewnego towaru obniżono najpierw o 30%, a następnie obniżono o 20% wodniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa A. 0,36 :x złotych. B. 0,44 :x złotych. C. 0,50 :x złotych. D. 0,56 : x złotych.

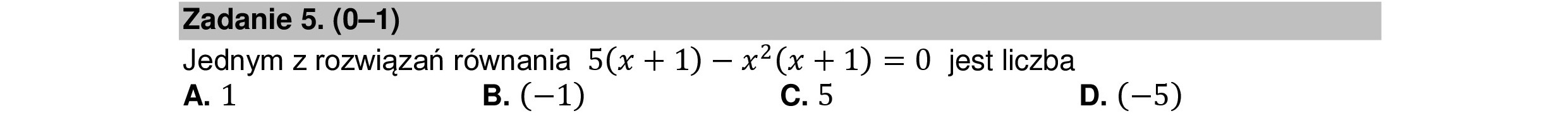
Zadanie 5. (0—1) Jednym z rozwiązań równania 5(x + 1) — x*(x + 1) =0 jest liczba A.1 B. (—1) Cc.5 D. (-5)


Zadanie 6. (0—1) Zbiorem wszystkich rozwiązań nierówności m - > 6x jest przedział A(-a-3) B(-Bso) | O(-m-3) | D(-$,o)

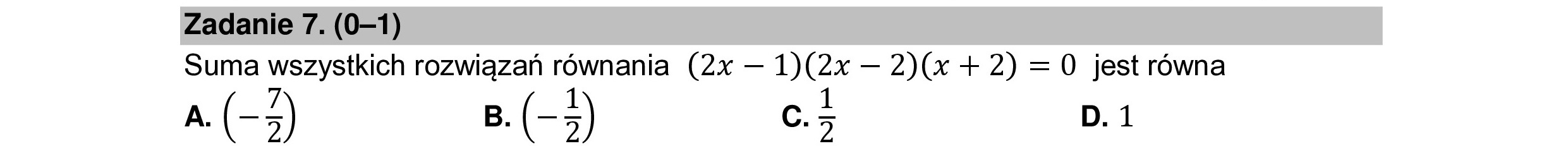
Zadanie 7. (0—1) Suma wszystkich rozwiązań równania (2x — 1)(2x — 2)(x + 2) =0 jest równa a. (-3) B. (-2) CE D.1

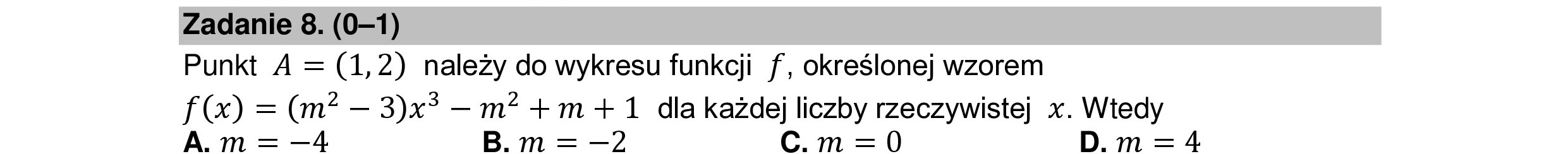
Zadanie 8. (0—1) Punkt A = (1,2) należy do wykresu funkcji f, określonej wzorem f(x) = (m* — 3)x* —m* +m+ 1 dla każdej liczby rzeczywistej x. Wtedy A.m =—4 B m=—2 c.m=0 D.m = 4

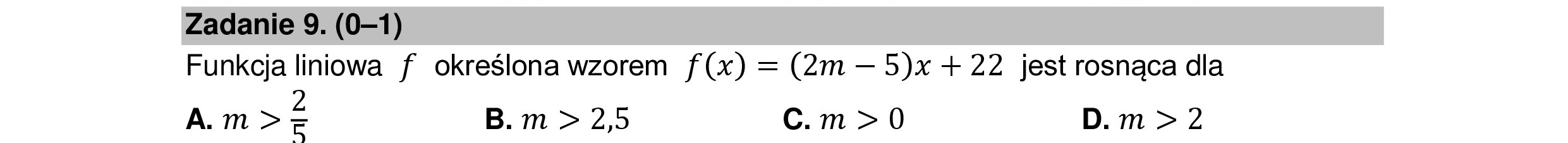
Zadanie 9. (0—1) Funkcja liniowa f określona wzorem f(x) = (2m — 5)x + 22 jest rosnąca dla A.m>Z B. m > 2,5 ccm>o0 D. m > 2


Zadanie 10. (0—1) Funkcja kwadratowa f określona wzorem f(x) = x? +bx +c osiąga dla x = 2 wartość najmniejszą równą 4. Wtedy A.b=—4, c=8 B.b=4, c=—8 C.b=—4, c=—8 D.b=4, c=8


Zadanie 11. (0—1) Dana jest funkcja kwadratowa f określona wzorem f(x) = —2(x — 2)(x + 1). Funkcja f jest rosnąca w zbiorze A. (—o, z) B. (—1,2) c. (0, 2) D. (+0)

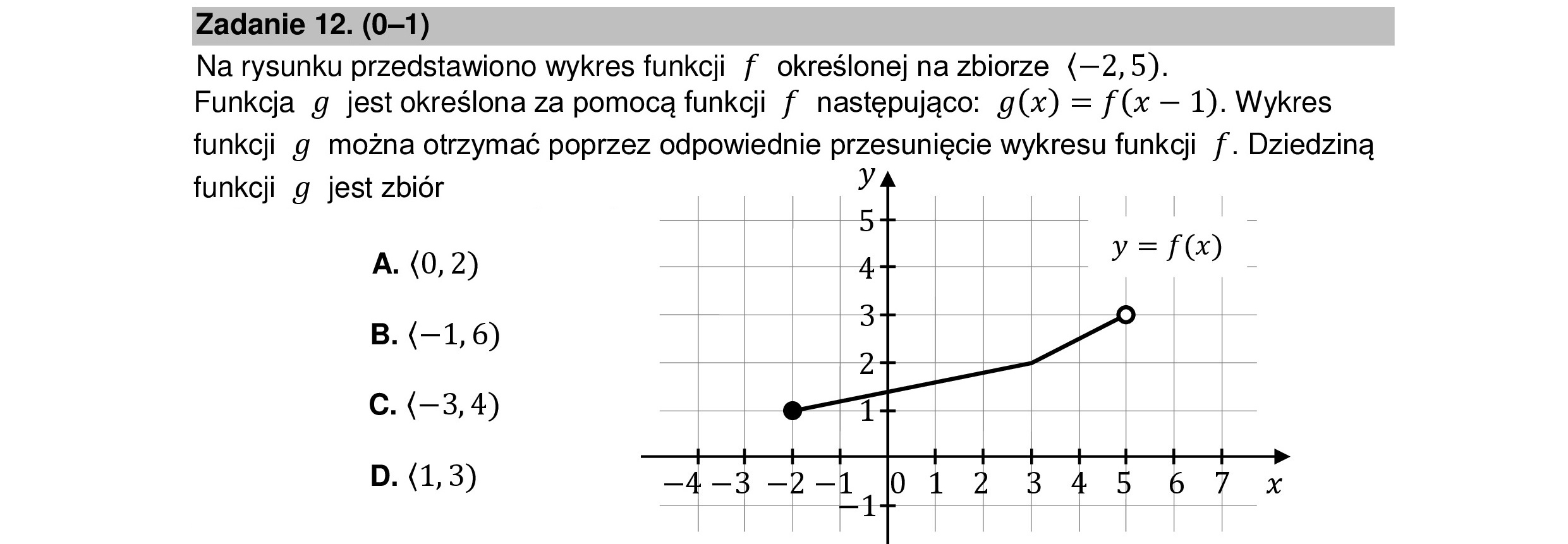
Zadanie 12. (0—1) Na rysunku przedstawiono wykres funkcji f określonej na zbiorze (—2,5). Funkcja g jest określona za pomocą funkcji f następująco: g(x) = f(x — 1). Wykres funkcji g można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji f. Dziedziną funkcji g_ jest zbiór y A. (0,2) B. (—1,6) C. (—3,4) D. (1,3)


Zadanie 13. (0—1) Dane są ciągi a, = 3n oraz b, = 4n — 2, określone dla każdej liczby naturalnej n > 1. Liczba 10 A. jest wyrazem ciągu (a,) i jest wyrazem ciągu (b,). B. jest wyrazem ciągu (a,) i nie jest wyrazem ciągu (b,). C. nie jest wyrazem ciągu (a,„) i jest wyrazem ciągu (b). D. nie jest wyrazem ciągu (a,) i nie jest wyrazem ciągu (b,).


Zadanie 14. (0—1) Dany jest ciąg geometryczny (a), określony dla każdej liczby naturalnej n > 1. Drugi wyraz tego ciągu oraz iloraz ciągu (a„) są równe 2. Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa A.1 B. 11 Cc. 21 D. 31


Zadanie 15. (0—1) W ciągu dwóch godzin trzy jednakowe maszyny produkują razem 1200 guzików. Ile guzików wyprodukuje pięć takich maszyn w ciągu jednej godziny? Przyjmij, że maszyny pracują z taką samą, stałą wydajnością. A. 800 B. 900 C. 1000 D. 1500


Zadanie 16. (0-1) Przyprostokątna AC trójkąta prostokątnego ABC ma długość 6, a przeciwprostokątna 4B ma długość 3V5. Wtedy tangens kąta ostrego CAB tego trójkąta jest równy /5 2/5 1 A. E B. —g c. 5 D. 2


Zadanie 17. (0—1) Nie istnieje kąt ostry a taki, że A. sina = C. sina =

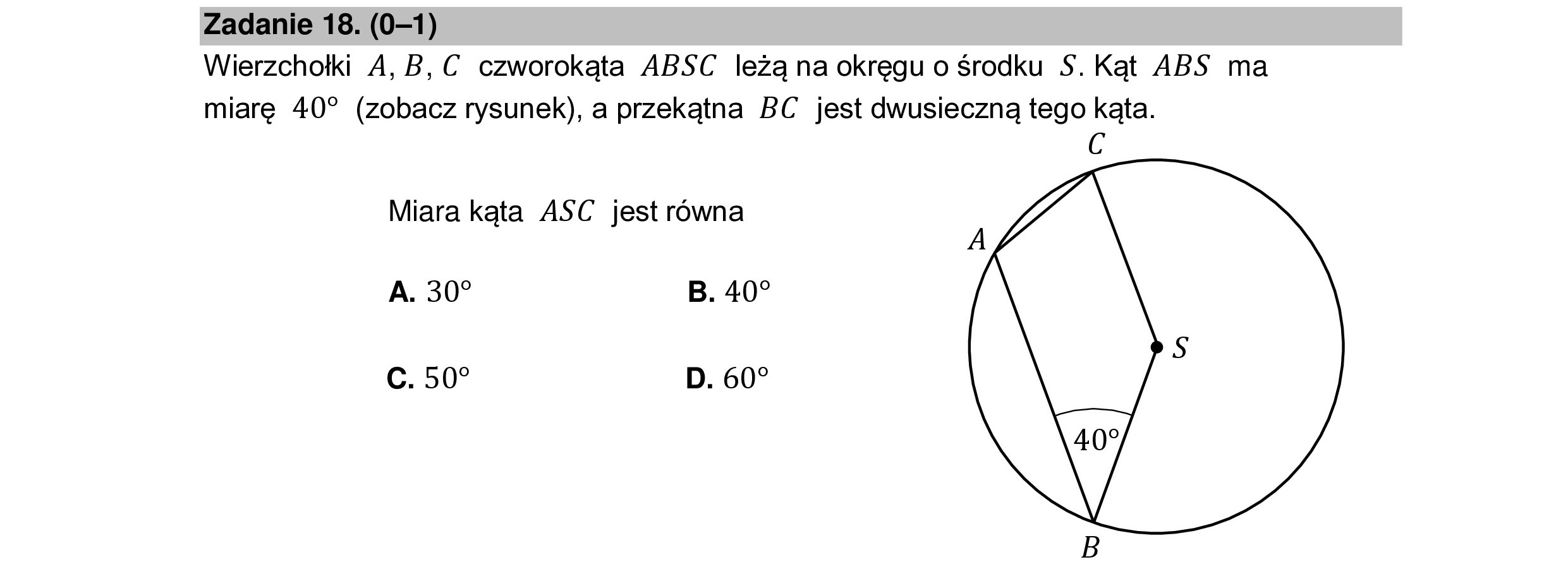
Zadanie 18. (0—1) Wierzchołki A, B, € czworokąta ABSC leżą na okręgu o środku S$. Kąt ABS ma miarę 40” (zobacz rysunek), a przekątna BC jest dwusieczną tego kąta. Miara kąta ASC jest równa , ZA A. 30? B. 40? Cc. 50” D. 60?

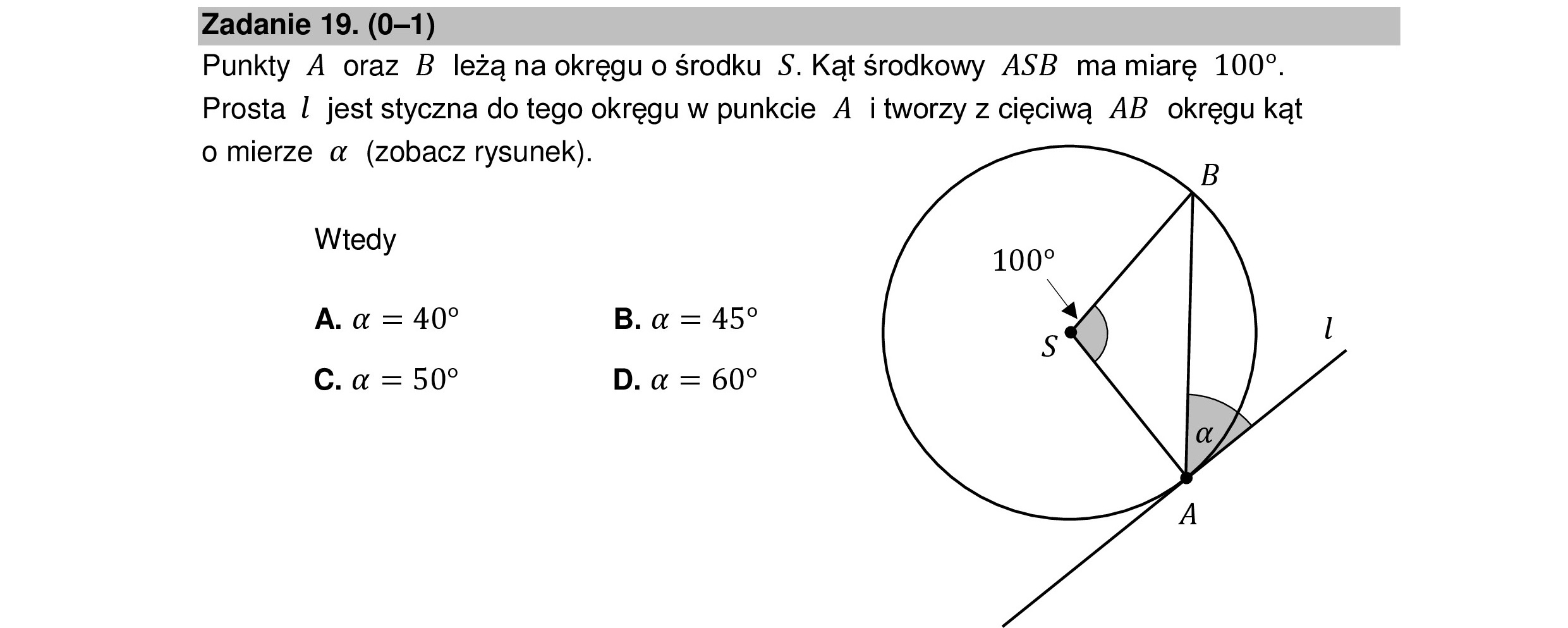
Zadanie 19. (0—1) Punkty A oraz B leżą na okręgu o środku S$. Kątśrodkowy ASB ma miarę 1007. Prosta l jest styczna do tego okręgu w punkcie A i tworzy z cięciwą AB okręgu kąt o mierze a (zobacz rysunek). Wtedy A.a =40 B. a = 459 C. a =507 D. a = 60?


Zadanie 20. (0—1) Pole prostokąta jest równe 16, a przekątne tego prostokąta przecinają się pod kątem ostrym a, takim, że sina = 0,2. Długość przekątnej tego prostokąta jest równa A. 4/5 B. 4/10 Cc. 80 D. 160

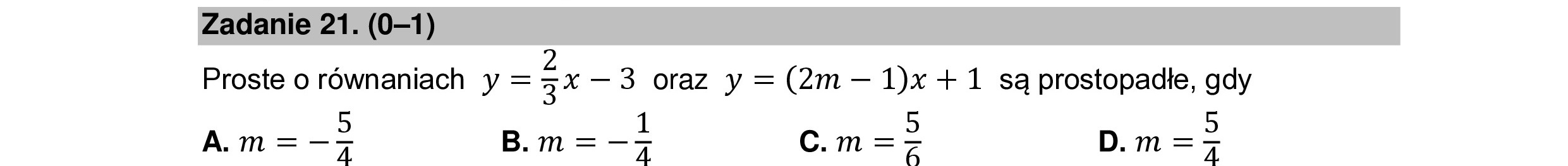
Zadanie 21. (0—1) Proste o równaniach y = zx —3 oraz y = (2m— 1)x +1 są prostopadłe, gdy 5 A.m=—q7 B.m=-l C.m=> D.m=>


Zadanie 22. (0—1) Punkty A = (1, —3) oraz C = (—2,4) są końcami przekątnej AC rombu ABCD. Środek przekątnej BD tego rombu ma współrzędne A. (-2. 2) B. (. -3) C. (—1,2) D. (—1,1)


Zadanie 23. (0—1) Punkty A = (—6,5),B = (5,7), C = (10, —3) są wierzchołkami równoległoboku ABCD. Długość przekątnej BD tego równoległoboku jest równa A. 3Y5 B. 4/5 C. 6Y5 D. 8V5

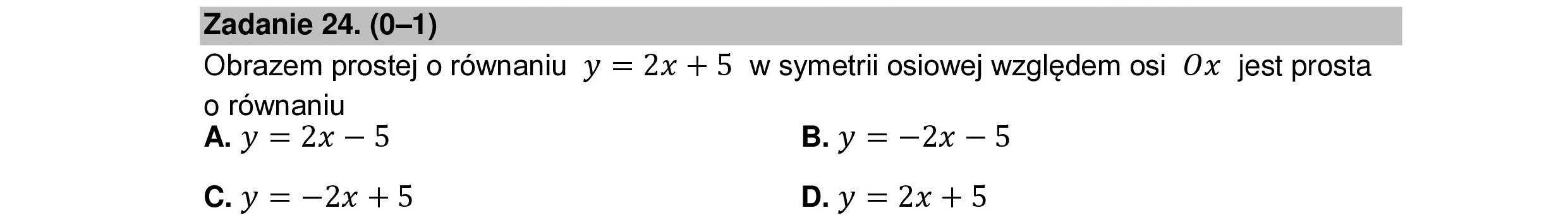
Zadanie 24. (0—1) Obrazem prostej o równaniu y = 2x + 5 w symetrii osiowej względem osi Ox jest prosta o równaniu A.y=2x-5 B.y=—2x—5 C.y=—2x +95 D.y=2x+5


Zadanie 25. (0—1) W graniastosłupie prawidłowym stosunek liczby wszystkich krawędzi do liczby wszystkich ścian jest równy 7 : 3. Podstawą tego graniastosłupa jest A. trójkąt. B. pięciokąt. C. siedmiokąt. D. ośmiokąt.


Zadanie 26. (0—1) Średnia arytmetyczna zestawu liczb a, b, c, d jest równa 20. Wtedy średnia arytmetyczna zestawu liczb a — 10, b + 30, c, d jest równa A. 10 B. 20 C. 25 D. 30


Zadanie 27. (0—1) Wszystkich trzycyfrowych liczb naturalnych większych od 300 o wszystkich cyfrach parzystych jest A.6-.10-10 B.3-10-10 C.6-:5-5 D.3:5:-5


Zadanie 28. (0—1) Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek — od jednego do sześciu. Niech p oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 3. Wtedy _1 _1 _1 _2

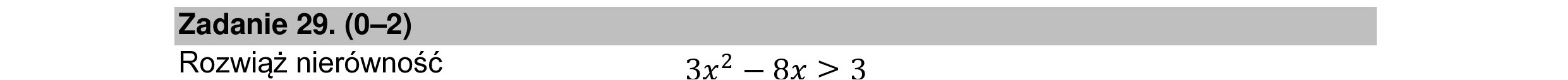
Zadanie 29. (0—2) Rozwiąż nierówność 2,2 _gy> 3


Zadanie 30. (0—2) Trójwyrazowy ciąg (x,y — 4,y) jest arytmetyczny. Suma wszystkich wyrazów tego ciągu jest równa 6. Oblicz wszystkie wyrazy tego ciągu.


Zadanie 31. (0—2) Wykaż, że dla każdej liczby rzeczywistej a różnej od 0 i każdej liczby rzeczywistej b różnej od 0 spełniona jest nierówność 2a2 — 4ab +£5b2 >0

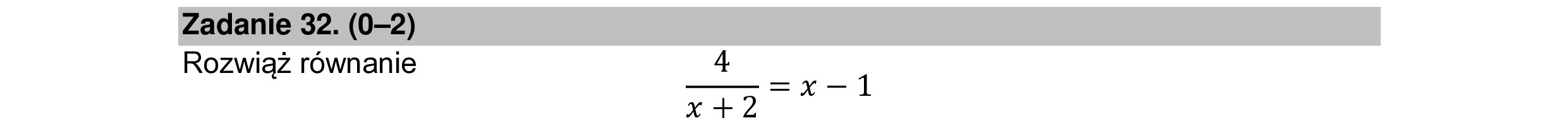
4 Rozwiąż równanie =x-1 «x -+L2 s

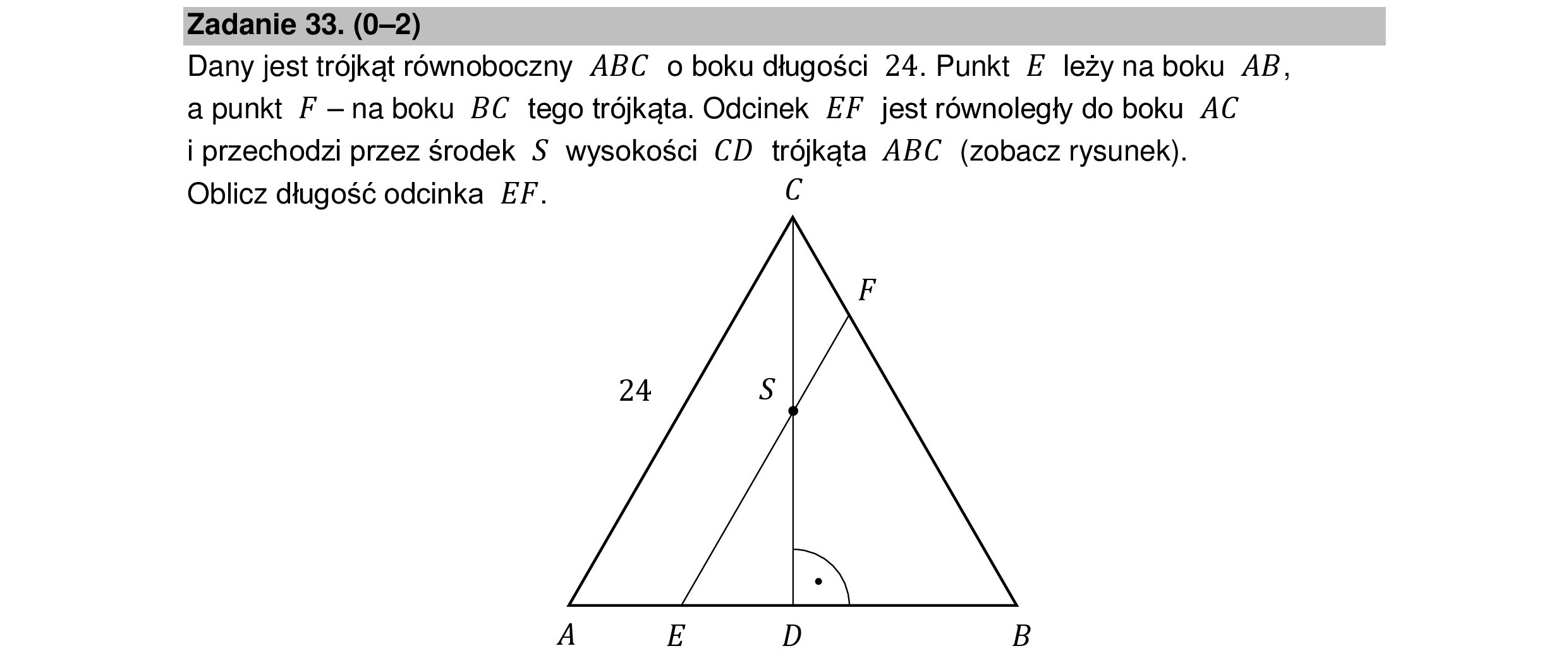
Zadanie 33. (0—2) Dany jest trójkąt równoboczny ABC o boku długości 24. Punkt E leży na boku 4B, a punkt F —naboku BC tego trójkąta. Odcinek EF jest równoległy do boku AC i przechodzi przez środek S wysokości CD trójkąta ABC (zobacz rysunek). Oblicz długość odcinka EF. C 24


Zadanie 34. (0-2) Ze zbioru pięciu liczb (—5, —4, 1, 2,3) losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie A polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia 4.


Zadanie 35. (0-5) Dany jest graniastosłup prosty ABCDEFGH, którego podstawą jest prostokąt ABCD. W tym graniastosłupie |BD| = 15, a ponadto |CD| = 3 + |BC| oraz |4.CDG| = 60” (zobacz rysunek). Oblicz objętość i pole powierzchni bocznej tego graniastosłupa.

MATEMATYKA 2022 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) —40 Liczba PUJ jest równa A, 474 B. 4770 Cc. 2747 D. 27130


Zadanie 2. (0-1) Liczba log» 32 — loga 8 jest równa A. 2 B. 14 C. 16 D. 24


Zadanie 3. (0-1) Liczba (5 — 2Y3) jest równa A. 25 +43 B. 25 — 4/3 C. 37 + 20V3 D. 37 — 20V3


Zadanie 4. (0—1) Cenę x (w złotych) pewnego towaru obniżono najpierw o 30%, a następnie obniżono o 20% wodniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa A. 0,36 :x złotych. B. 0,44 :x złotych. C. 0,50 :x złotych. D. 0,56 : x złotych.

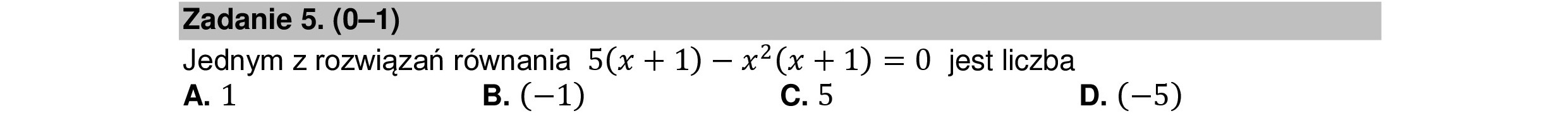
Zadanie 5. (0—1) Jednym z rozwiązań równania 5(x + 1) — x*(x + 1) =0 jest liczba A.1 B. (—1) Cc.5 D. (-5)


Zadanie 6. (0—1) Zbiorem wszystkich rozwiązań nierówności m - > 6x jest przedział A(-a-3) B(-Bso) | O(-m-3) | D(-$,o)

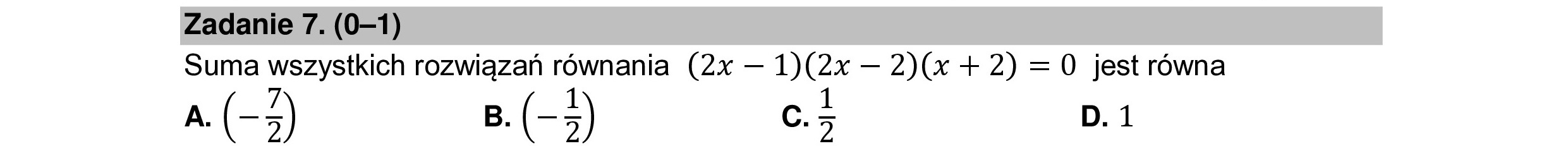
Zadanie 7. (0—1) Suma wszystkich rozwiązań równania (2x — 1)(2x — 2)(x + 2) =0 jest równa a. (-3) B. (-2) CE D.1

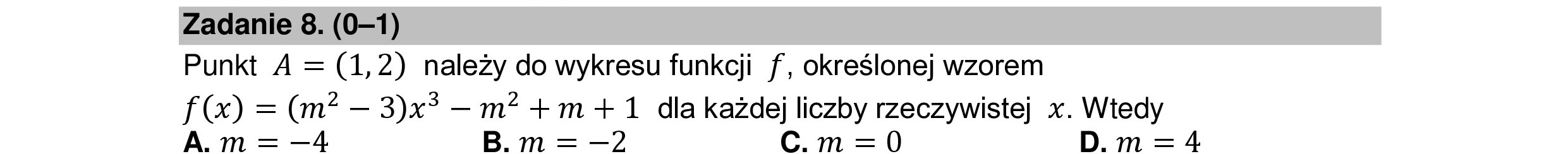
Zadanie 8. (0—1) Punkt A = (1,2) należy do wykresu funkcji f, określonej wzorem f(x) = (m* — 3)x* —m* +m+ 1 dla każdej liczby rzeczywistej x. Wtedy A.m =—4 B m=—2 c.m=0 D.m = 4

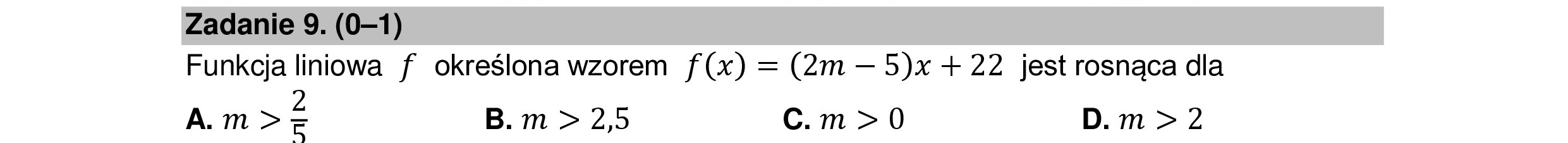
Zadanie 9. (0—1) Funkcja liniowa f określona wzorem f(x) = (2m — 5)x + 22 jest rosnąca dla A.m>Z B. m > 2,5 ccm>o0 D. m > 2


Zadanie 10. (0—1) Funkcja kwadratowa f określona wzorem f(x) = x? +bx +c osiąga dla x = 2 wartość najmniejszą równą 4. Wtedy A.b=—4, c=8 B.b=4, c=—8 C.b=—4, c=—8 D.b=4, c=8


Zadanie 11. (0—1) Dana jest funkcja kwadratowa f określona wzorem f(x) = —2(x — 2)(x + 1). Funkcja f jest rosnąca w zbiorze A. (—o, z) B. (—1,2) c. (0, 2) D. (+0)


Zadanie 12. (0—1) Na rysunku przedstawiono wykres funkcji f określonej na zbiorze (—2,5). Funkcja g jest określona za pomocą funkcji f następująco: g(x) = f(x — 1). Wykres funkcji g można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji f. Dziedziną funkcji g_ jest zbiór y A. (0,2) B. (—1,6) C. (—3,4) D. (1,3)


Zadanie 13. (0—1) Dane są ciągi a, = 3n oraz b, = 4n — 2, określone dla każdej liczby naturalnej n > 1. Liczba 10 A. jest wyrazem ciągu (a,) i jest wyrazem ciągu (b,). B. jest wyrazem ciągu (a,) i nie jest wyrazem ciągu (b,). C. nie jest wyrazem ciągu (a,„) i jest wyrazem ciągu (b). D. nie jest wyrazem ciągu (a,) i nie jest wyrazem ciągu (b,).


Zadanie 14. (0—1) Dany jest ciąg geometryczny (a), określony dla każdej liczby naturalnej n > 1. Drugi wyraz tego ciągu oraz iloraz ciągu (a„) są równe 2. Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa A.1 B. 11 Cc. 21 D. 31


Zadanie 15. (0—1) W ciągu dwóch godzin trzy jednakowe maszyny produkują razem 1200 guzików. Ile guzików wyprodukuje pięć takich maszyn w ciągu jednej godziny? Przyjmij, że maszyny pracują z taką samą, stałą wydajnością. A. 800 B. 900 C. 1000 D. 1500


Zadanie 16. (0-1) Przyprostokątna AC trójkąta prostokątnego ABC ma długość 6, a przeciwprostokątna 4B ma długość 3V5. Wtedy tangens kąta ostrego CAB tego trójkąta jest równy /5 2/5 1 A. E B. —g c. 5 D. 2


Zadanie 17. (0—1) Nie istnieje kąt ostry a taki, że A. sina = C. sina =


Zadanie 18. (0—1) Wierzchołki A, B, € czworokąta ABSC leżą na okręgu o środku S$. Kąt ABS ma miarę 40” (zobacz rysunek), a przekątna BC jest dwusieczną tego kąta. Miara kąta ASC jest równa , ZA A. 30? B. 40? Cc. 50” D. 60?


Zadanie 19. (0—1) Punkty A oraz B leżą na okręgu o środku S$. Kątśrodkowy ASB ma miarę 1007. Prosta l jest styczna do tego okręgu w punkcie A i tworzy z cięciwą AB okręgu kąt o mierze a (zobacz rysunek). Wtedy A.a =40 B. a = 459 C. a =507 D. a = 60?


Zadanie 20. (0—1) Pole prostokąta jest równe 16, a przekątne tego prostokąta przecinają się pod kątem ostrym a, takim, że sina = 0,2. Długość przekątnej tego prostokąta jest równa A. 4/5 B. 4/10 Cc. 80 D. 160

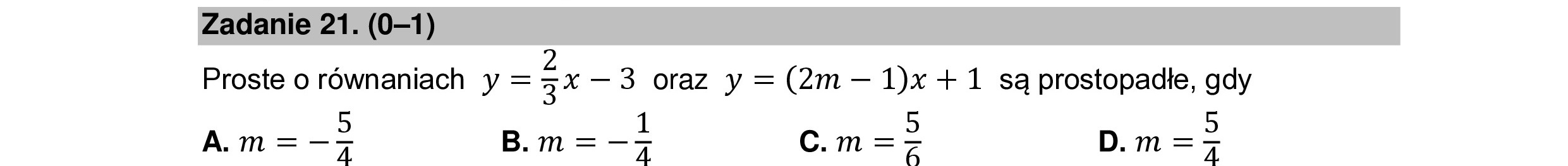
Zadanie 21. (0—1) Proste o równaniach y = zx —3 oraz y = (2m— 1)x +1 są prostopadłe, gdy 5 A.m=—q7 B.m=-l C.m=> D.m=>


Zadanie 22. (0—1) Punkty A = (1, —3) oraz C = (—2,4) są końcami przekątnej AC rombu ABCD. Środek przekątnej BD tego rombu ma współrzędne A. (-2. 2) B. (. -3) C. (—1,2) D. (—1,1)


Zadanie 23. (0—1) Punkty A = (—6,5),B = (5,7), C = (10, —3) są wierzchołkami równoległoboku ABCD. Długość przekątnej BD tego równoległoboku jest równa A. 3Y5 B. 4/5 C. 6Y5 D. 8V5

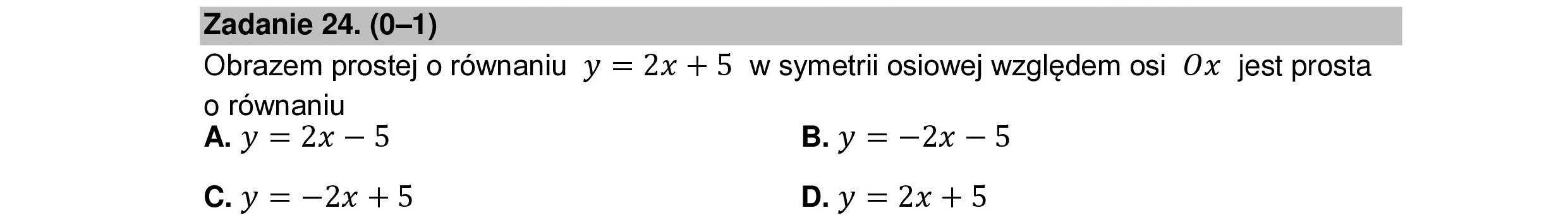
Zadanie 24. (0—1) Obrazem prostej o równaniu y = 2x + 5 w symetrii osiowej względem osi Ox jest prosta o równaniu A.y=2x-5 B.y=—2x—5 C.y=—2x +95 D.y=2x+5


Zadanie 25. (0—1) W graniastosłupie prawidłowym stosunek liczby wszystkich krawędzi do liczby wszystkich ścian jest równy 7 : 3. Podstawą tego graniastosłupa jest A. trójkąt. B. pięciokąt. C. siedmiokąt. D. ośmiokąt.


Zadanie 26. (0—1) Średnia arytmetyczna zestawu liczb a, b, c, d jest równa 20. Wtedy średnia arytmetyczna zestawu liczb a — 10, b + 30, c, d jest równa A. 10 B. 20 C. 25 D. 30


Zadanie 27. (0—1) Wszystkich trzycyfrowych liczb naturalnych większych od 300 o wszystkich cyfrach parzystych jest A.6-.10-10 B.3-10-10 C.6-:5-5 D.3:5:-5


Zadanie 28. (0—1) Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek — od jednego do sześciu. Niech p oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 3. Wtedy _1 _1 _1 _2

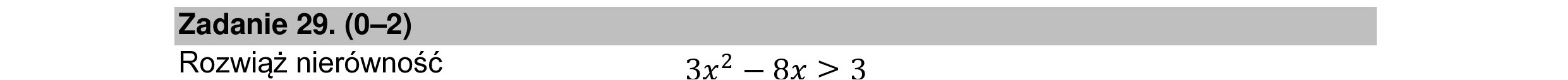
Zadanie 29. (0—2) Rozwiąż nierówność 2,2 _gy> 3


Zadanie 30. (0—2) Trójwyrazowy ciąg (x,y — 4,y) jest arytmetyczny. Suma wszystkich wyrazów tego ciągu jest równa 6. Oblicz wszystkie wyrazy tego ciągu.


Zadanie 31. (0—2) Wykaż, że dla każdej liczby rzeczywistej a różnej od 0 i każdej liczby rzeczywistej b różnej od 0 spełniona jest nierówność 2a2 — 4ab +£5b2 >0

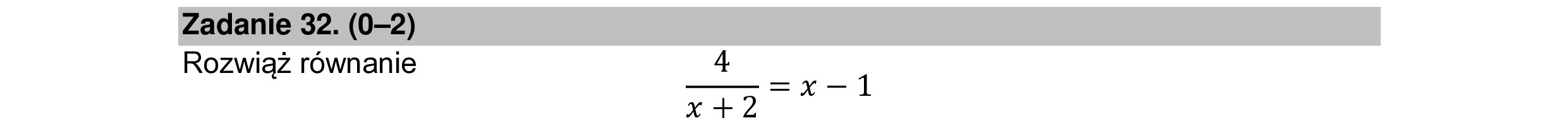
4 Rozwiąż równanie =x-1 «x -+L2 s


Zadanie 33. (0—2) Dany jest trójkąt równoboczny ABC o boku długości 24. Punkt E leży na boku 4B, a punkt F —naboku BC tego trójkąta. Odcinek EF jest równoległy do boku AC i przechodzi przez środek S wysokości CD trójkąta ABC (zobacz rysunek). Oblicz długość odcinka EF. C 24


Zadanie 34. (0-2) Ze zbioru pięciu liczb (—5, —4, 1, 2,3) losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie A polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia 4.


Zadanie 35. (0-5) Dany jest graniastosłup prosty ABCDEFGH, którego podstawą jest prostokąt ABCD. W tym graniastosłupie |BD| = 15, a ponadto |CD| = 3 + |BC| oraz |4.CDG| = 60” (zobacz rysunek). Oblicz objętość i pole powierzchni bocznej tego graniastosłupa.






























