MATEMATYKA 2021 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) Liczba 919 -. 319 jest równa A. 27? B. 9? 37 D.31


Zadanie 2. (0—1) Liczba logę 9 + 2 log, 2 jest równa A. log67 B.1 Cc. 2 D. log i


Zadanie 3. (0-1) Liczba x stanowi 80% liczby dodatniej y. Wynika stąd, że liczba y to A. 125% liczby x. B. 120% liczby x. C. 25% liczby x. D. 20% liczby x.

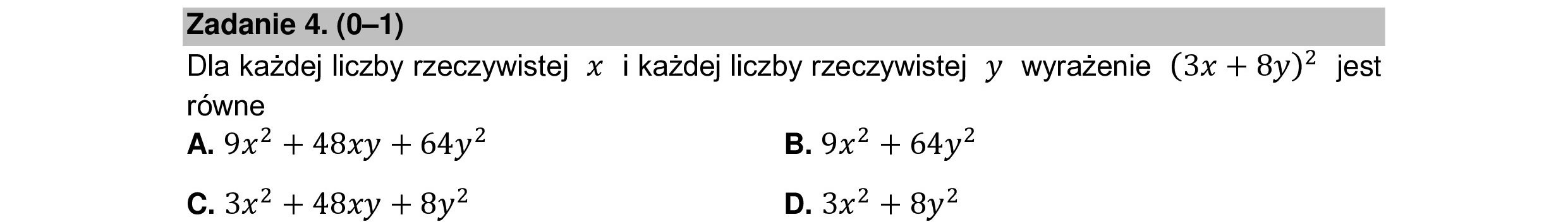
Zadanie 4. (0—1) Dla każdej liczby rzeczywistej x i każdej liczby rzeczywistej y wyrażenie (3x + 8y)? jest równe A. 9x” + 48xy + 64y? B. 9x? + 64y? C. 3x? + 48xy + 8y? D. 3x? + 8y?


Zadanie 5. (0-1) Liczba (—2) jest rozwiązaniem równania x+2 A.x*+4=0 B.——=1 C.zzz=0 D.x2(ć +2)+2(x+2)=0


Zadanie 6. (0—1) Zbiorem wszystkich rozwiązań nierówności 5 — > > 2x +1 jest przedział A. (o, 1) B. (1, +00) Cc. (—o, 7) D. (7, +oo)


Zadanie 7. (0—1) Funkcja liniowa f jest określona wzorem f(x) = —2x + 4. Wykres funkcji f przesunięto wzdłuż osi Ox o 2 jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji g. Funkcja g jest określona wzorem A. g(x) = —2x +2 B. g(x) = —2x C. g(x) = —2x +6 D. g(x) = —2x +8

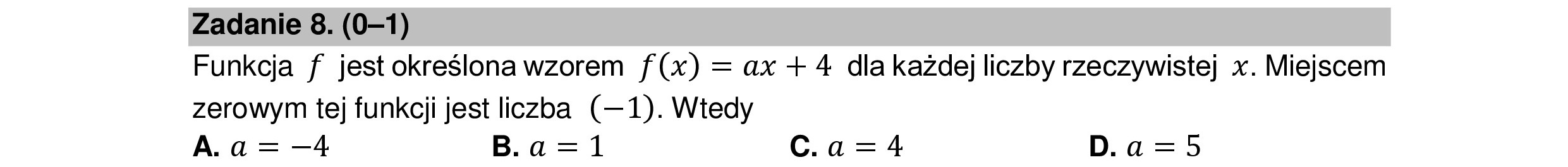
Zadanie 8. (0—1) Funkcja f jest określona wzorem f(x) = ax +4 dla każdej liczby rzeczywistej x. Miejscem zerowym tej funkcji jest liczba (—1). Wtedy A.a= —4 B.a=1 C.a=4 D.a=5

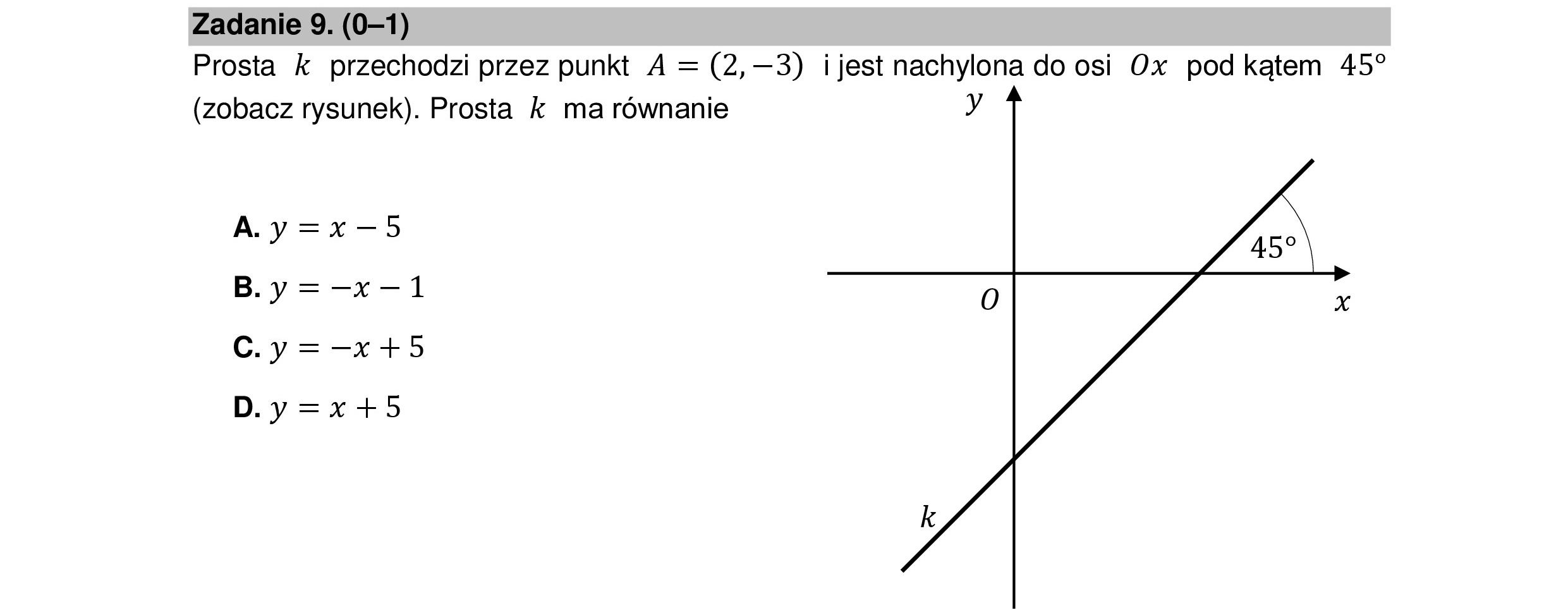
Zadanie 9. (0—1) Prosta k przechodzi przez punkt A = (2, —3) i jest nachylona do osi Ox pod kątem 45? (zobacz rysunek). Prosta k ma równanie A.y=x-5 B.y=—x-1 Cy=—x+5 D.y=x+5


Zadanie 10. (0-1) Funkcja kwadratowa f jest określona wzorem f(x) = —2(x + 3)(x — 5). Wierzchołek paraboli, która jest wykresem funkcji f, ma współrzędną x równą A. (—3) B. (—1) c.1 D. 5

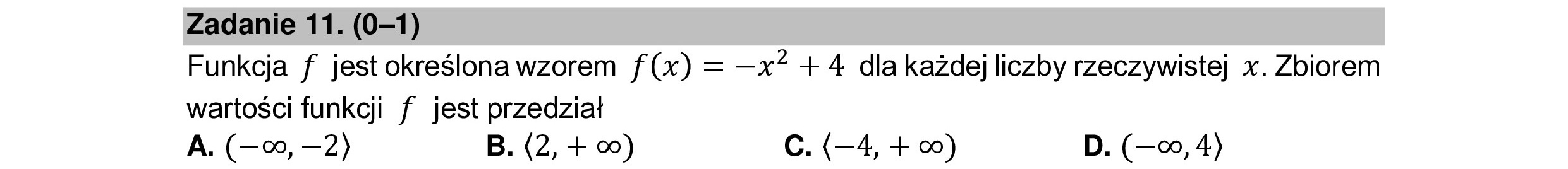
Zadanie 11. (0—1) Funkcja f jest określona wzorem f(x) = —x? +4 dla każdej liczby rzeczywistej x. Zbiorem wartości funkcji f jest przedział A. (—0, —2) B. (2, + 00) C. (—4, + o) D. (—0,4)

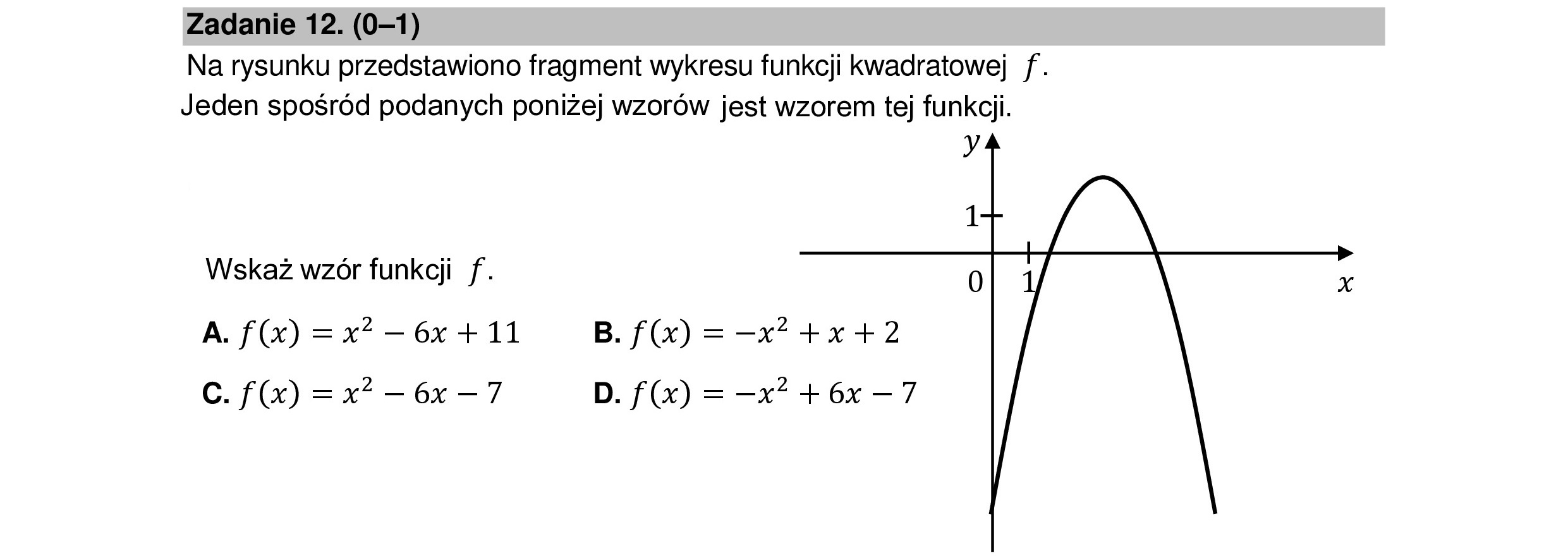
Zadanie 12. (0—1) Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f. Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji f. A. f(x) =x*—6x+11 B. f(x) =—x*+x+2 C. f(x) =x* —6x—7 D. f(x) = —x* + 6x —7


Zadanie 13. (0—1) Ciąg arytmetyczny (a,) jest określony dla każdej liczby naturalnej n > 1. Różnica tego ciągu jest równa 2. Wtedy A. dą — ag = 18 B. a>4 — ag = 20 C. dą — Qę = 36 D. A>4 — ag = 38


Zadanie 14. (0—1) Suma wszystkich liczb całkowitych dodatnich parzystych i jednocześnie mniejszych od 1001 jest równa A. a 499 B. M. 500 c. ie 500 D. Eh. 1001


Zadanie 15. (0—1) Trójwyrazowy ciąg (2, x, 18) jest rosnącym ciągiem geometrycznym. Wtedy A.x=16 B.x=10 C.x=6 D.x=9


Zadanie 16. (0-1) Kąt a jestostryi sina = A Wynika stąd, że 576 24 24 18 A. Cosa = zo5 B. cos a = >5 C. cos a = — 75 D. cos a = 55

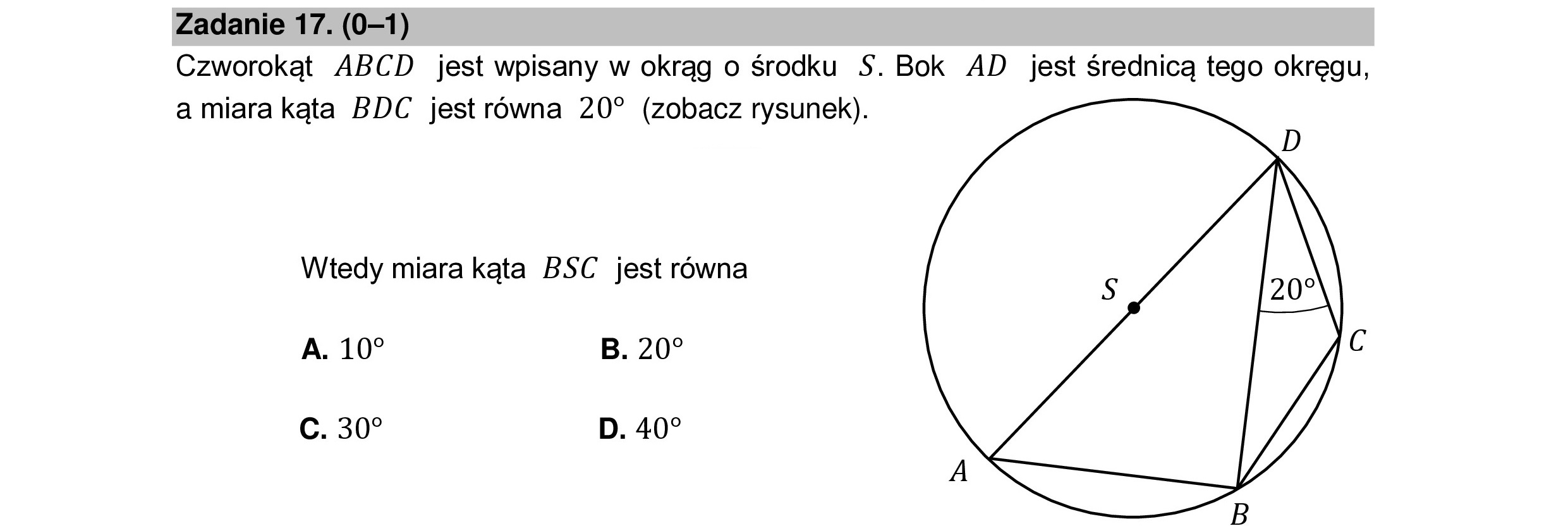
Zadanie 17. (0—1) Czworokąt ABCD jest wpisany w okrąg o środku S$. Bok AD jest średnicą tego okręgu, a miara kąta BDC jest równa 20? (zobacz rysunek). Wtedy miara kąta BSC jest równa A. 10? B. 207 Cc. 30” D. 40”

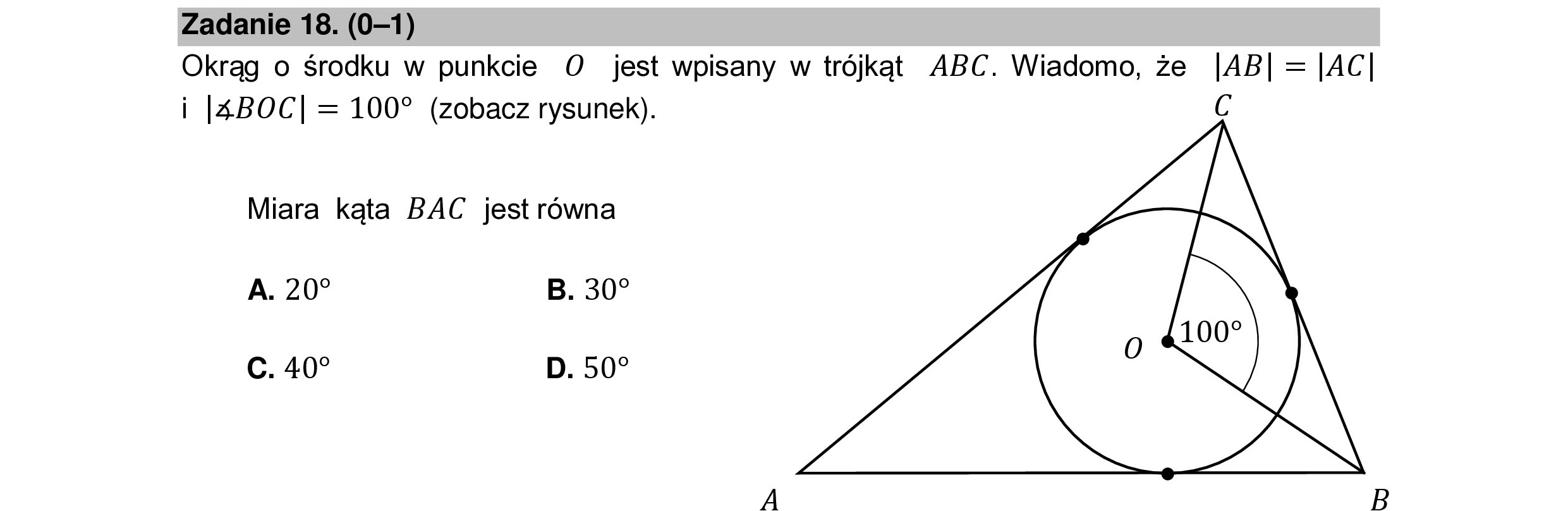
Zadanie 18. (0—1) Okrąg o środku w punkcie O jest wpisany w trójkąt ABC. Wiadomo, że |AB|=|AC| i |4BOC| = 100” (zobacz rysunek). G Miara kąta BAC jest równa ZN A. 20? B. 30? c. 40” D. 50?

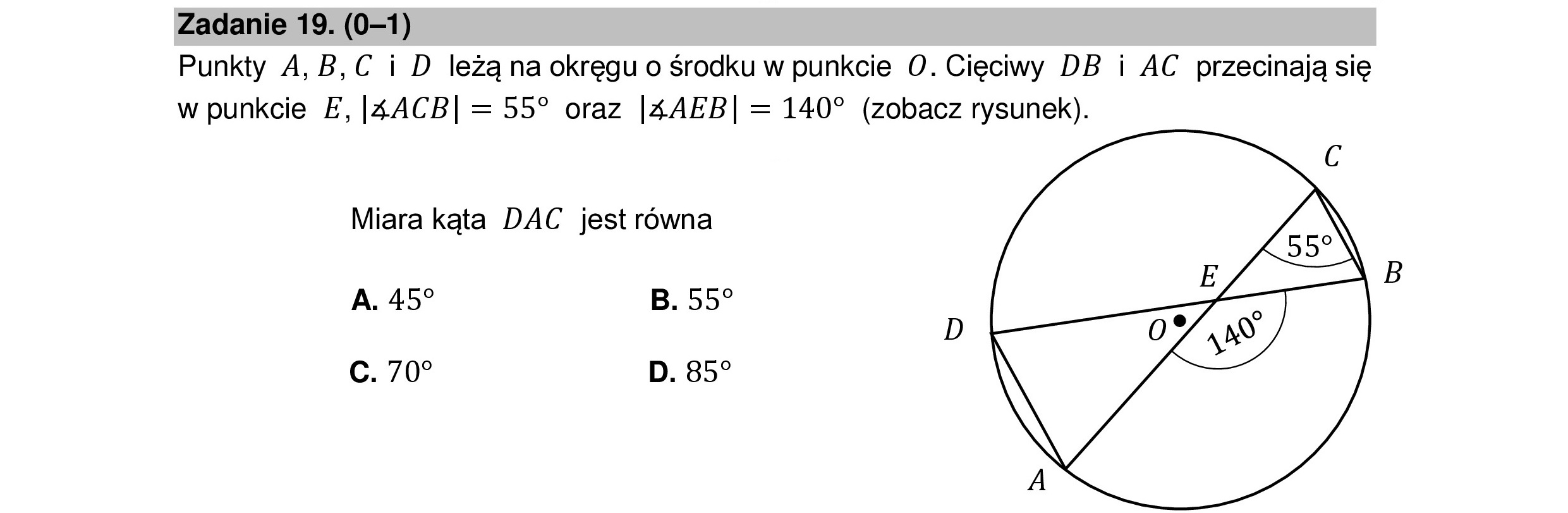
Zadanie 19. (0-1) Punkty A,B,C i D leżą na okręgu o środku w punkcie O. Cięciwy DB i AC przecinają się w punkcie E, |4ACB| = 55? oraz |4AEB| = 140? (zobacz rysunek). C Miara kąta DAC jest równa ZAŃ /__—ĄB A. 452 B. 552 D Żys) D. 85? c. 70”

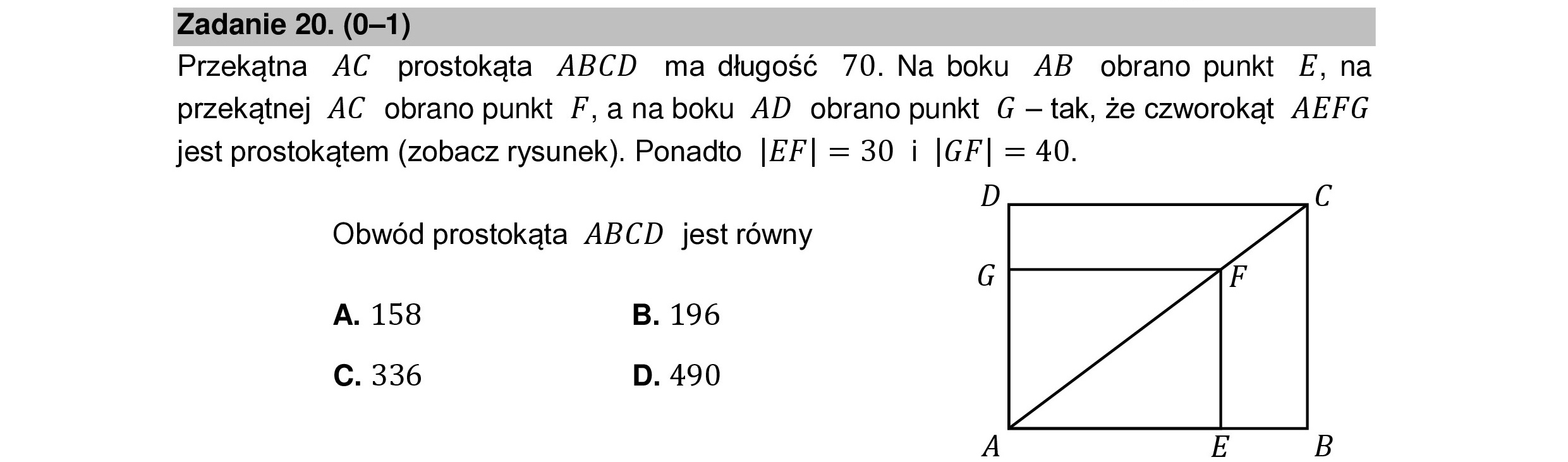
Zadanie 20. (0—1) Przekątna AC prostokąta ABCD ma długość 70. Na boku AB obrano punkt E, na przekątnej AC obrano punkt F, anaboku AD obrano punkt G — tak, że czworokąt AEFG jest prostokątem (zobacz rysunek). Ponadto |EF| = 30 i |GF| = 40. D C Obwód prostokąta ABCD jest równy EESESA G A. 158 B. 196 C. 336 D. 490

Zadanie 21. (0—1) W układzie współrzędnych dane są dwa punkty A = (1, —2) oraz B = (3,1). Współczynnik kierunkowy prostej AB jest równy A. (->) B. (-Z) c.Ż D. NI W


Zadanie 22. (0-1) Prosta k ma równanie y= x + 24. Współczynnik kierunkowy prostej prostopadłej do prostej k jest równy A.7 B. (-2) c.(-7) D. 4 R


Zadanie 23. (0—1) Punkty A = (3,7) i C = (—4,6) są końcami przekątnej kwadratu ABCD. Promień okręgu opisanego na tym kwadracie jest równy A. B. E Cc. A 7 D. 5


Zadanie 24. (0—1) Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 2 (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe A. 24+2Y3 B. 24+ 6V3 C. 24+12V3 D. 24 + 24/3


Zadanie 25. (0—1) Przekątna sześcianu jest równa 6. Wynika stąd, że objętość tego sześcianu jest równa A. 24/3 B. 72 C. 54/2 D. 6484/3


Zadanie 26. (0—1) Wszystkich liczb naturalnych pięciocyfrowych parzystych jest A.9-2-10* B.9-5.-103 C.5-10* D. 4 - 10?


Zadanie 27. (0—1) W pudełku znajdują się tylko kule białe i kule czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 3 : 4. Wylosowanie każdej kuli z tego pudełka jest jednakowo prawdopodobne. Losujemy jedną kulę. Niech A oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia A jest równe 1 1 3 3 A. 7 B. 7 C. 5 D. 7


Zadanie 28. (0—1) Średnia arytmetyczna pięciu liczb: 5x + 6, 6x +7, 7x +8, 8x +9, 9x + 10, jestrówna 8. Wtedy x jest równe A. (—35) B.0 C. 0,35 D. 35

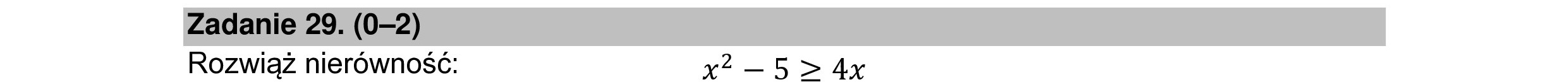
Zadanie 29. (0—2) Rozwiąż nierówność:

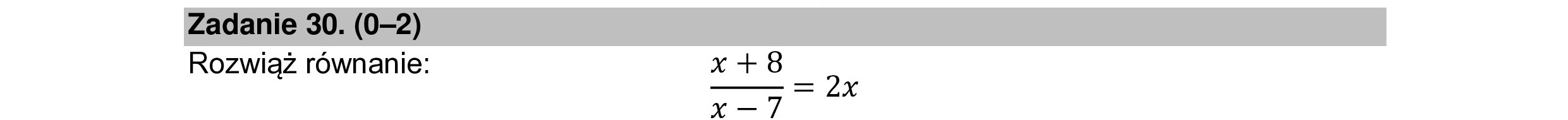
Rozwiąż równanie:


Zadanie 31. (0—2) Wykaż, że dla każdej liczby rzeczywistej a i każdej liczby rzeczywistej b spełniona jest nierówność b(5b —4a)+a?>0

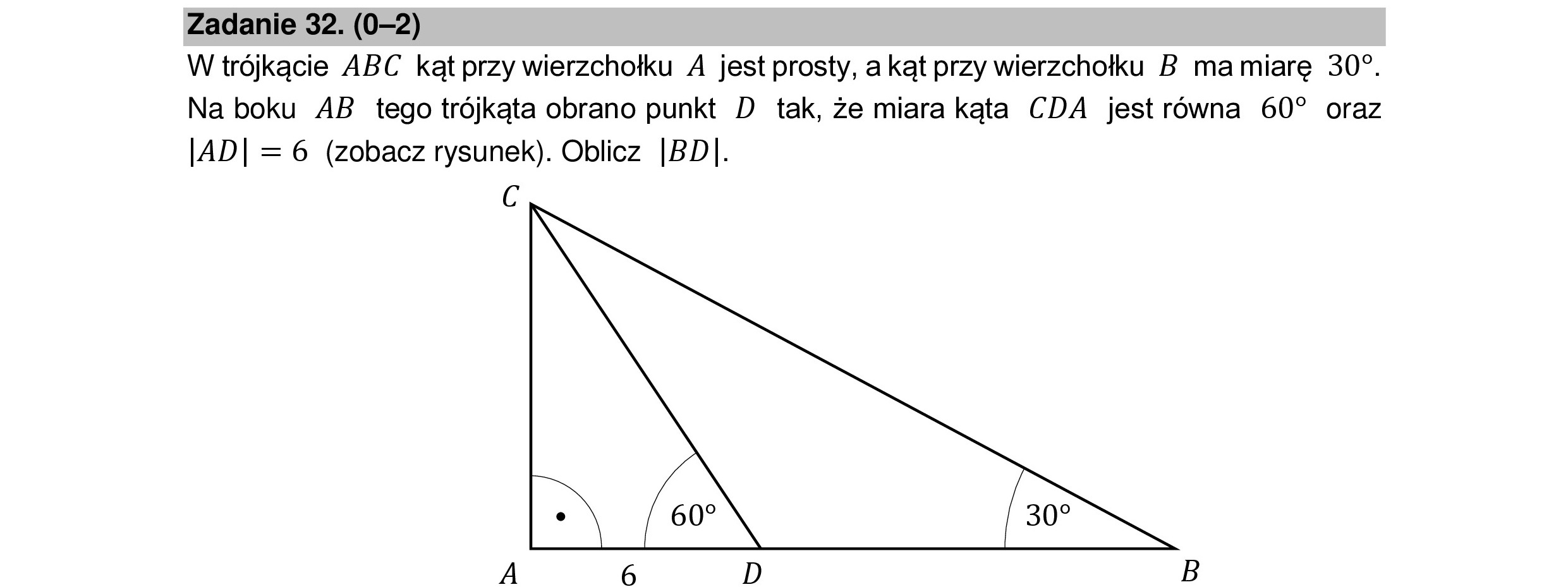
Zadanie 32. (0-2) W trójkącie ABC kąt przy wierzchołku 4 jest prosty, a kąt przy wierzchołku B mamiarę 30". Na boku AB tego trójkąta obrano punkt D tak, że miara kąta CDA jest równa 60” oraz |[AD| = 6 (zobacz rysunek). Oblicz |BD|. C

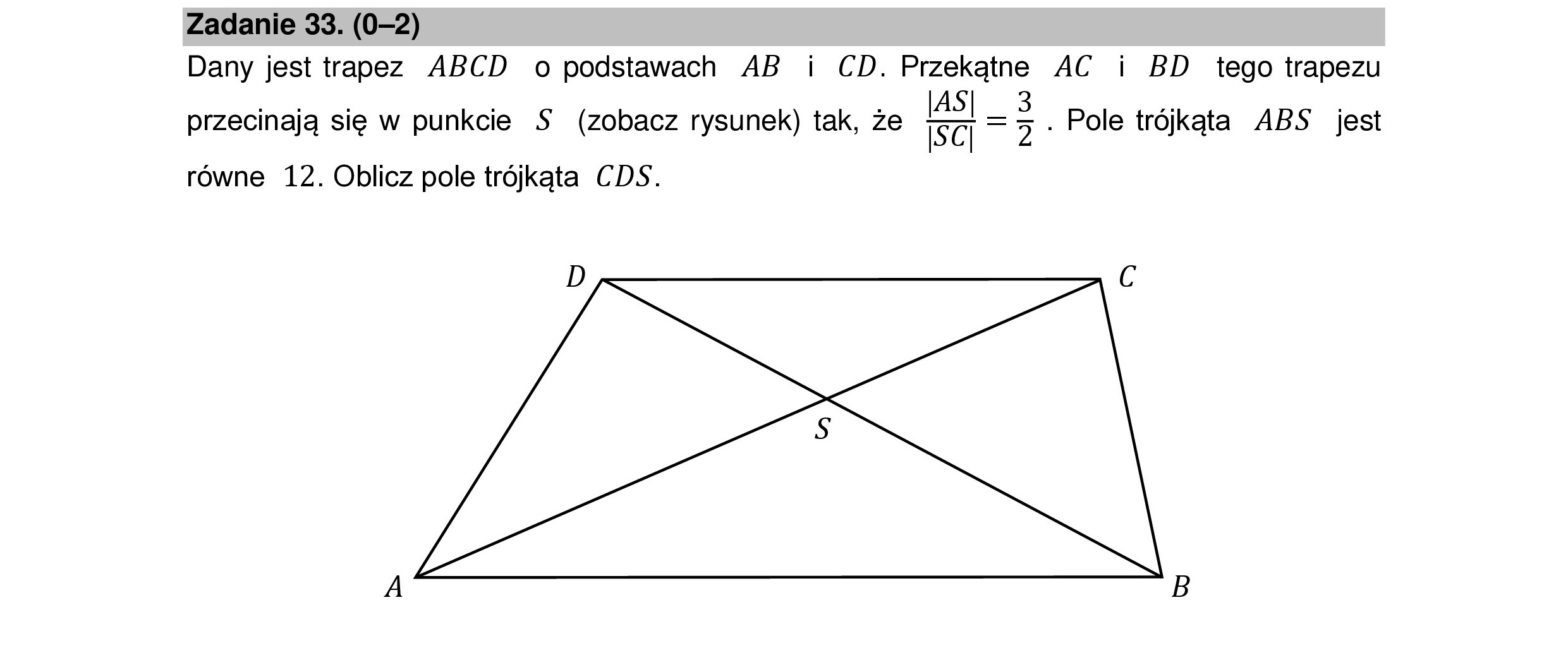
Zadanie 33. (0-2) Dany jest trapez ABCD o podstawach AB i CD. Przekątne AC i BD tego trapezu przecinają się w punkcie S (zobacz rysunek) tak, że se = . Pole trójkąta ABS jest równe 12. Oblicz pole trójkąta CDS. D C


Zadanie 34. (0-2) Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek — od jednego do sześciu oczek. Niech 4 oznacza zdarzenie polegające na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach jest równy 12. Oblicz prawdopodobieństwo zdarzenia 4.


Zadanie 35. (0-5) Dany jest ciąg (a„) określony wzorem a, = m dla każdej liczby naturalnej n> 1. Trójwyrazowy ciąg (a, ,x? + 2,a4,), gdzie x jest liczbą rzeczywistą, jest geometryczny. Oblicz x oraz iloraz tego ciągu geometrycznego.

MATEMATYKA 2021 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) Liczba 919 -. 319 jest równa A. 27? B. 9? 37 D.31


Zadanie 2. (0—1) Liczba logę 9 + 2 log, 2 jest równa A. log67 B.1 Cc. 2 D. log i


Zadanie 3. (0-1) Liczba x stanowi 80% liczby dodatniej y. Wynika stąd, że liczba y to A. 125% liczby x. B. 120% liczby x. C. 25% liczby x. D. 20% liczby x.

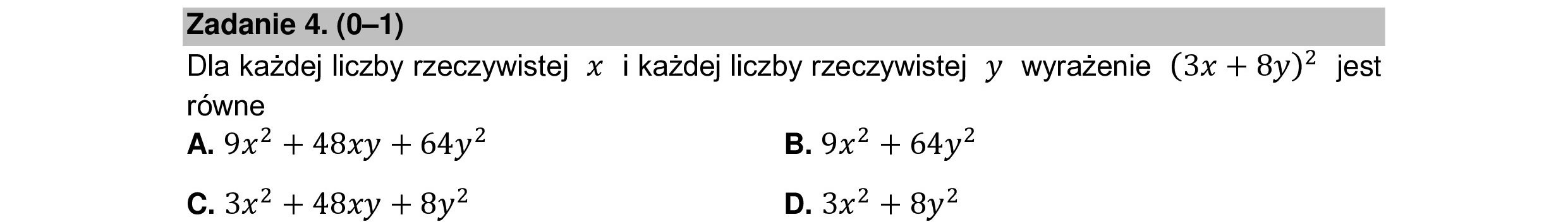
Zadanie 4. (0—1) Dla każdej liczby rzeczywistej x i każdej liczby rzeczywistej y wyrażenie (3x + 8y)? jest równe A. 9x” + 48xy + 64y? B. 9x? + 64y? C. 3x? + 48xy + 8y? D. 3x? + 8y?


Zadanie 5. (0-1) Liczba (—2) jest rozwiązaniem równania x+2 A.x*+4=0 B.——=1 C.zzz=0 D.x2(ć +2)+2(x+2)=0


Zadanie 6. (0—1) Zbiorem wszystkich rozwiązań nierówności 5 — > > 2x +1 jest przedział A. (o, 1) B. (1, +00) Cc. (—o, 7) D. (7, +oo)


Zadanie 7. (0—1) Funkcja liniowa f jest określona wzorem f(x) = —2x + 4. Wykres funkcji f przesunięto wzdłuż osi Ox o 2 jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji g. Funkcja g jest określona wzorem A. g(x) = —2x +2 B. g(x) = —2x C. g(x) = —2x +6 D. g(x) = —2x +8

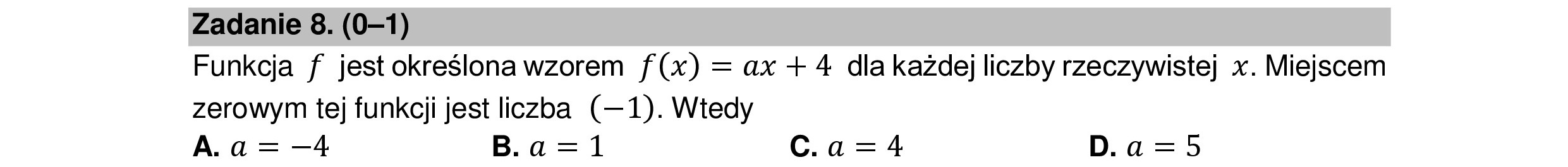
Zadanie 8. (0—1) Funkcja f jest określona wzorem f(x) = ax +4 dla każdej liczby rzeczywistej x. Miejscem zerowym tej funkcji jest liczba (—1). Wtedy A.a= —4 B.a=1 C.a=4 D.a=5


Zadanie 9. (0—1) Prosta k przechodzi przez punkt A = (2, —3) i jest nachylona do osi Ox pod kątem 45? (zobacz rysunek). Prosta k ma równanie A.y=x-5 B.y=—x-1 Cy=—x+5 D.y=x+5


Zadanie 10. (0-1) Funkcja kwadratowa f jest określona wzorem f(x) = —2(x + 3)(x — 5). Wierzchołek paraboli, która jest wykresem funkcji f, ma współrzędną x równą A. (—3) B. (—1) c.1 D. 5

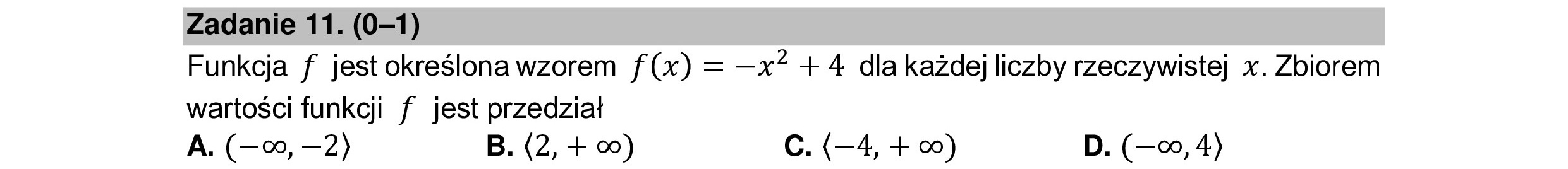
Zadanie 11. (0—1) Funkcja f jest określona wzorem f(x) = —x? +4 dla każdej liczby rzeczywistej x. Zbiorem wartości funkcji f jest przedział A. (—0, —2) B. (2, + 00) C. (—4, + o) D. (—0,4)


Zadanie 12. (0—1) Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f. Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji f. A. f(x) =x*—6x+11 B. f(x) =—x*+x+2 C. f(x) =x* —6x—7 D. f(x) = —x* + 6x —7


Zadanie 13. (0—1) Ciąg arytmetyczny (a,) jest określony dla każdej liczby naturalnej n > 1. Różnica tego ciągu jest równa 2. Wtedy A. dą — ag = 18 B. a>4 — ag = 20 C. dą — Qę = 36 D. A>4 — ag = 38


Zadanie 14. (0—1) Suma wszystkich liczb całkowitych dodatnich parzystych i jednocześnie mniejszych od 1001 jest równa A. a 499 B. M. 500 c. ie 500 D. Eh. 1001


Zadanie 15. (0—1) Trójwyrazowy ciąg (2, x, 18) jest rosnącym ciągiem geometrycznym. Wtedy A.x=16 B.x=10 C.x=6 D.x=9


Zadanie 16. (0-1) Kąt a jestostryi sina = A Wynika stąd, że 576 24 24 18 A. Cosa = zo5 B. cos a = >5 C. cos a = — 75 D. cos a = 55


Zadanie 17. (0—1) Czworokąt ABCD jest wpisany w okrąg o środku S$. Bok AD jest średnicą tego okręgu, a miara kąta BDC jest równa 20? (zobacz rysunek). Wtedy miara kąta BSC jest równa A. 10? B. 207 Cc. 30” D. 40”


Zadanie 18. (0—1) Okrąg o środku w punkcie O jest wpisany w trójkąt ABC. Wiadomo, że |AB|=|AC| i |4BOC| = 100” (zobacz rysunek). G Miara kąta BAC jest równa ZN A. 20? B. 30? c. 40” D. 50?


Zadanie 19. (0-1) Punkty A,B,C i D leżą na okręgu o środku w punkcie O. Cięciwy DB i AC przecinają się w punkcie E, |4ACB| = 55? oraz |4AEB| = 140? (zobacz rysunek). C Miara kąta DAC jest równa ZAŃ /__—ĄB A. 452 B. 552 D Żys) D. 85? c. 70”


Zadanie 20. (0—1) Przekątna AC prostokąta ABCD ma długość 70. Na boku AB obrano punkt E, na przekątnej AC obrano punkt F, anaboku AD obrano punkt G — tak, że czworokąt AEFG jest prostokątem (zobacz rysunek). Ponadto |EF| = 30 i |GF| = 40. D C Obwód prostokąta ABCD jest równy EESESA G A. 158 B. 196 C. 336 D. 490

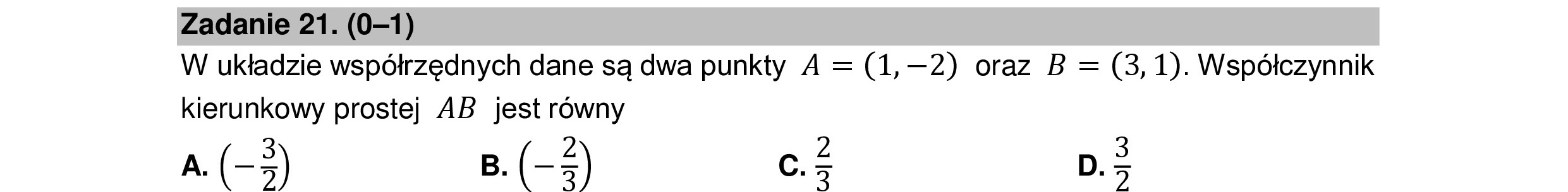
Zadanie 21. (0—1) W układzie współrzędnych dane są dwa punkty A = (1, —2) oraz B = (3,1). Współczynnik kierunkowy prostej AB jest równy A. (->) B. (-Z) c.Ż D. NI W


Zadanie 22. (0-1) Prosta k ma równanie y= x + 24. Współczynnik kierunkowy prostej prostopadłej do prostej k jest równy A.7 B. (-2) c.(-7) D. 4 R


Zadanie 23. (0—1) Punkty A = (3,7) i C = (—4,6) są końcami przekątnej kwadratu ABCD. Promień okręgu opisanego na tym kwadracie jest równy A. B. E Cc. A 7 D. 5


Zadanie 24. (0—1) Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 2 (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe A. 24+2Y3 B. 24+ 6V3 C. 24+12V3 D. 24 + 24/3


Zadanie 25. (0—1) Przekątna sześcianu jest równa 6. Wynika stąd, że objętość tego sześcianu jest równa A. 24/3 B. 72 C. 54/2 D. 6484/3


Zadanie 26. (0—1) Wszystkich liczb naturalnych pięciocyfrowych parzystych jest A.9-2-10* B.9-5.-103 C.5-10* D. 4 - 10?


Zadanie 27. (0—1) W pudełku znajdują się tylko kule białe i kule czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 3 : 4. Wylosowanie każdej kuli z tego pudełka jest jednakowo prawdopodobne. Losujemy jedną kulę. Niech A oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia A jest równe 1 1 3 3 A. 7 B. 7 C. 5 D. 7


Zadanie 28. (0—1) Średnia arytmetyczna pięciu liczb: 5x + 6, 6x +7, 7x +8, 8x +9, 9x + 10, jestrówna 8. Wtedy x jest równe A. (—35) B.0 C. 0,35 D. 35

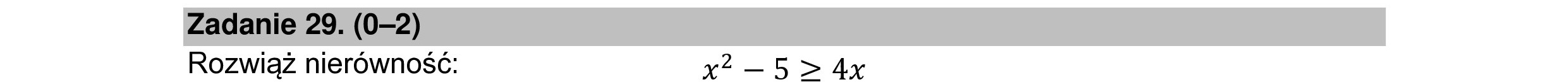
Zadanie 29. (0—2) Rozwiąż nierówność:

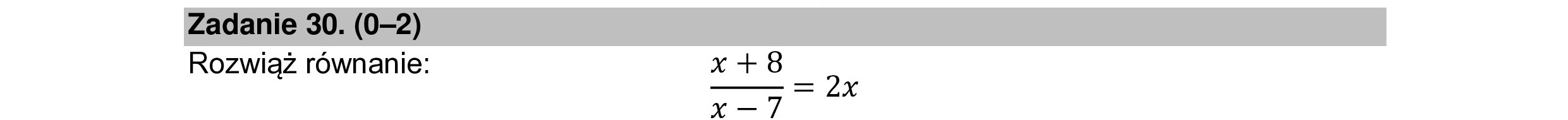
Rozwiąż równanie:


Zadanie 31. (0—2) Wykaż, że dla każdej liczby rzeczywistej a i każdej liczby rzeczywistej b spełniona jest nierówność b(5b —4a)+a?>0


Zadanie 32. (0-2) W trójkącie ABC kąt przy wierzchołku 4 jest prosty, a kąt przy wierzchołku B mamiarę 30". Na boku AB tego trójkąta obrano punkt D tak, że miara kąta CDA jest równa 60” oraz |[AD| = 6 (zobacz rysunek). Oblicz |BD|. C


Zadanie 33. (0-2) Dany jest trapez ABCD o podstawach AB i CD. Przekątne AC i BD tego trapezu przecinają się w punkcie S (zobacz rysunek) tak, że se = . Pole trójkąta ABS jest równe 12. Oblicz pole trójkąta CDS. D C


Zadanie 34. (0-2) Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek — od jednego do sześciu oczek. Niech 4 oznacza zdarzenie polegające na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach jest równy 12. Oblicz prawdopodobieństwo zdarzenia 4.


Zadanie 35. (0-5) Dany jest ciąg (a„) określony wzorem a, = m dla każdej liczby naturalnej n> 1. Trójwyrazowy ciąg (a, ,x? + 2,a4,), gdzie x jest liczbą rzeczywistą, jest geometryczny. Oblicz x oraz iloraz tego ciągu geometrycznego.






























