MATEMATYKA 2021 MAJ MATURA PODSTAWOWA

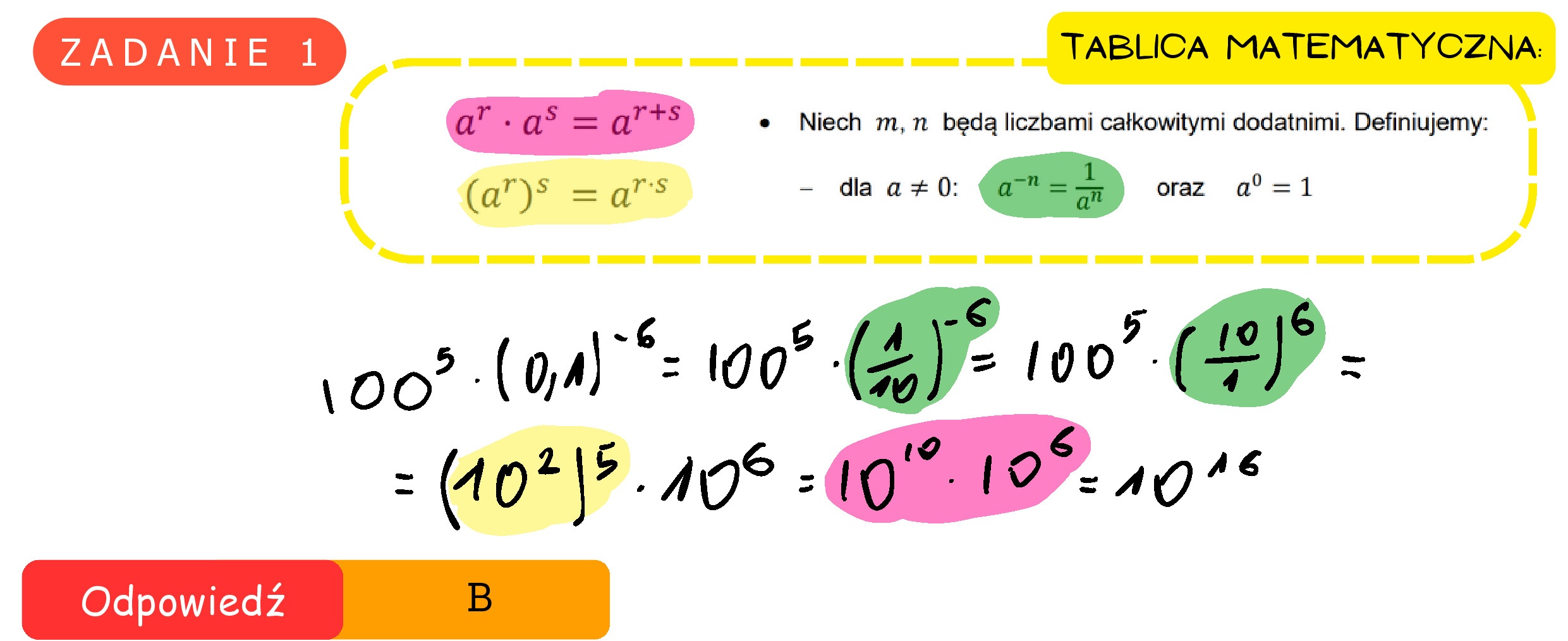
Zadanie 1. (0-1) Liczba 1007 - (0,1)"* jest równa A. 103 B. 1016 c. 1071 D. 1030
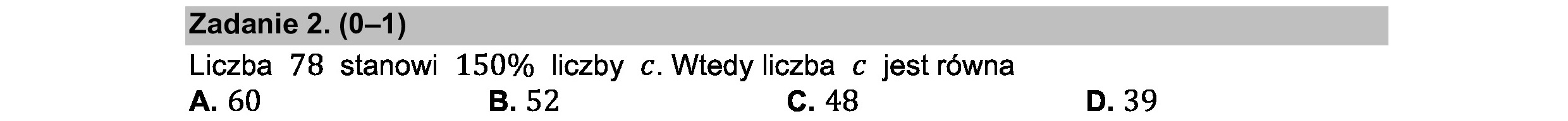
Zadanie 2. (0—1) Liczba 78 stanowi 150% liczby c. Wtedy liczba c jest równa A. 60 B. 52 C. 48 D. 39


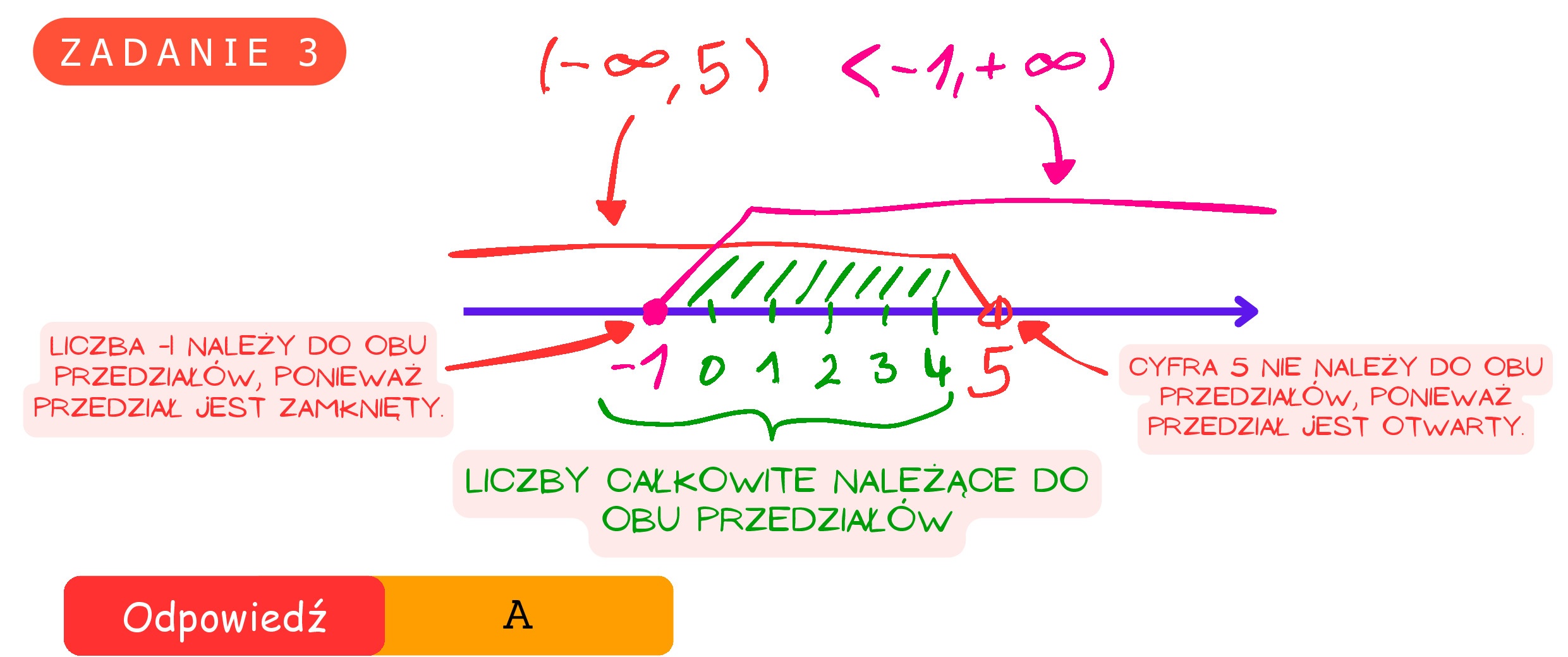
Zadanie 3. (0-1) Rozważamy przedziały liczbowe (—0,5) i (—1 +00). Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu rozważanych przedziałów? A. 6 B. 5 Cc. 4 D. 7

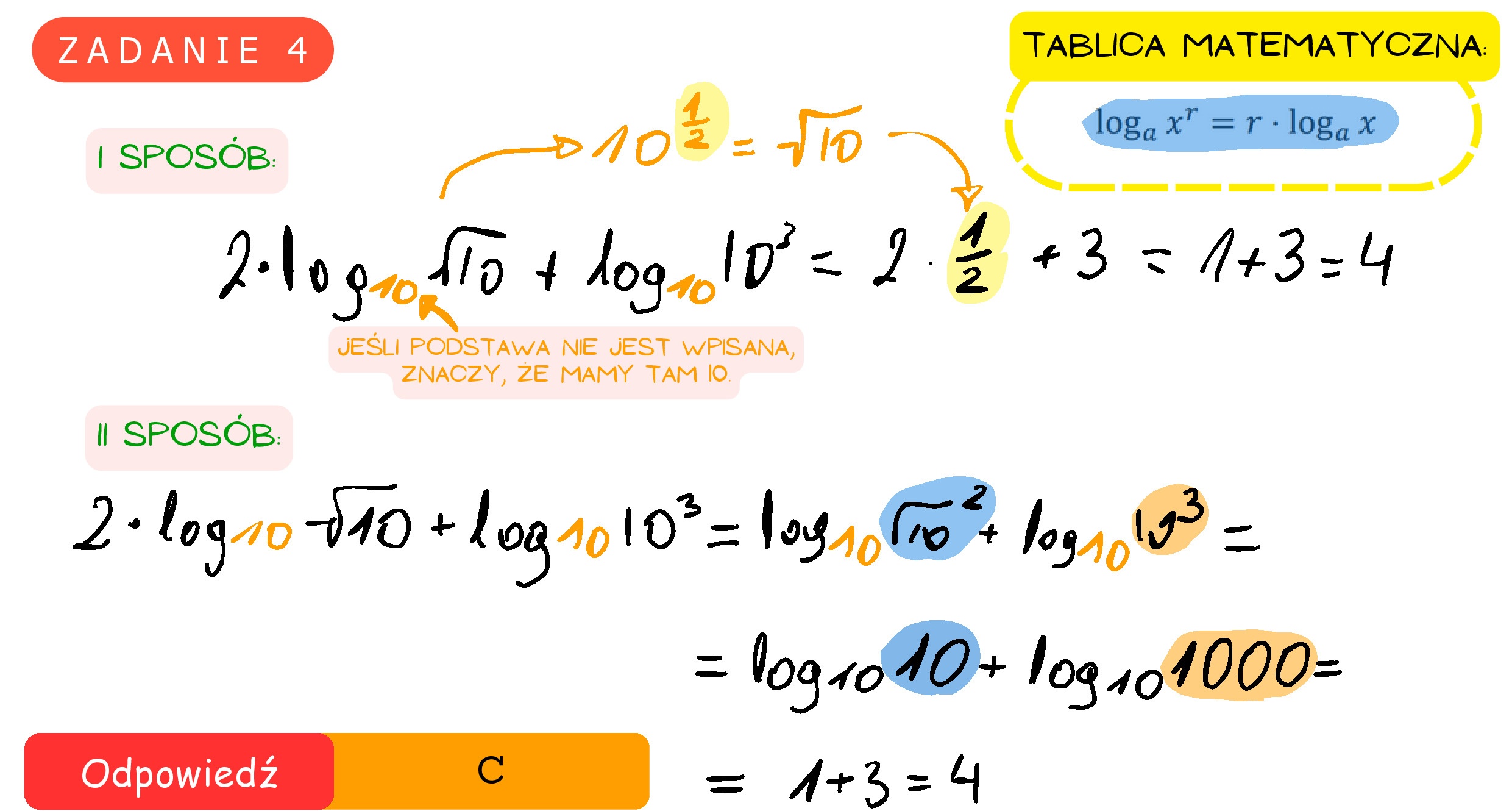
Zadanie 4. (0-1) Suma 2logv10 + log 10? jest równa A. 2 B. 3 D. 5

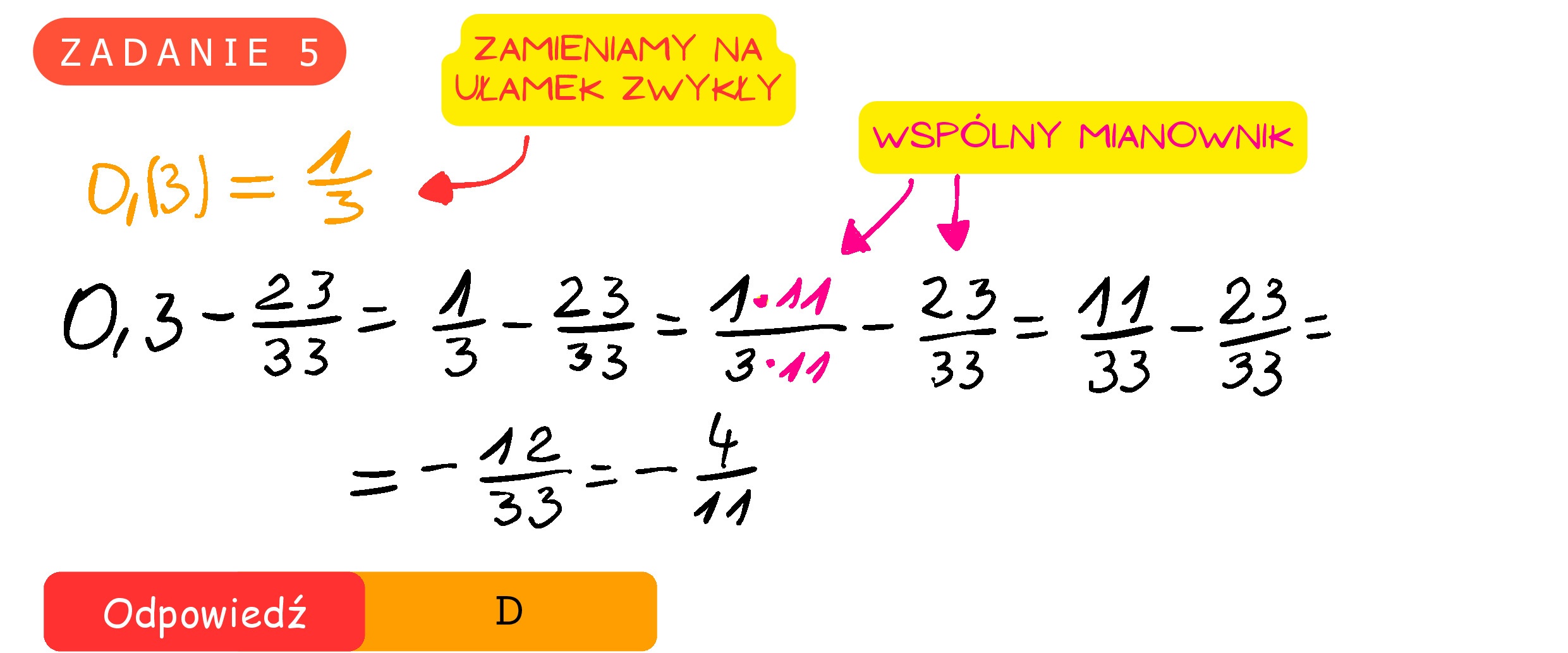
Zadanie 5. (0—1) Różnica 0,(3) — A. —0,(39) 23 33 jest równa B.- 39 100 Cc. —0,36
Zadanie 6. (0—1) Zbiorem wszystkich rozwiązań nierówności R — 2x2 1 jest przedział A. (0, +00) B. (—0, 0) C. (—0,5) D. (—a, 3)

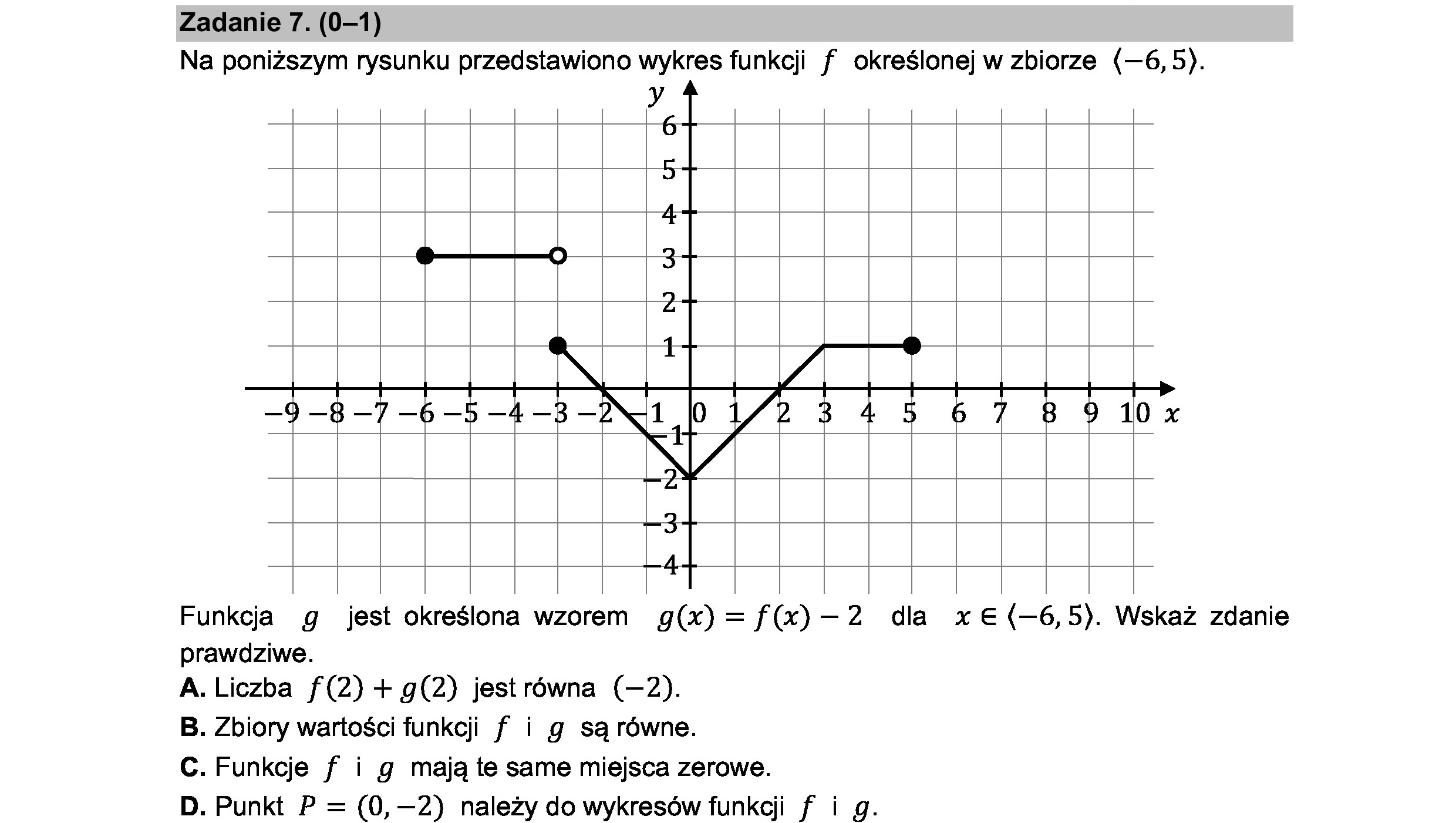
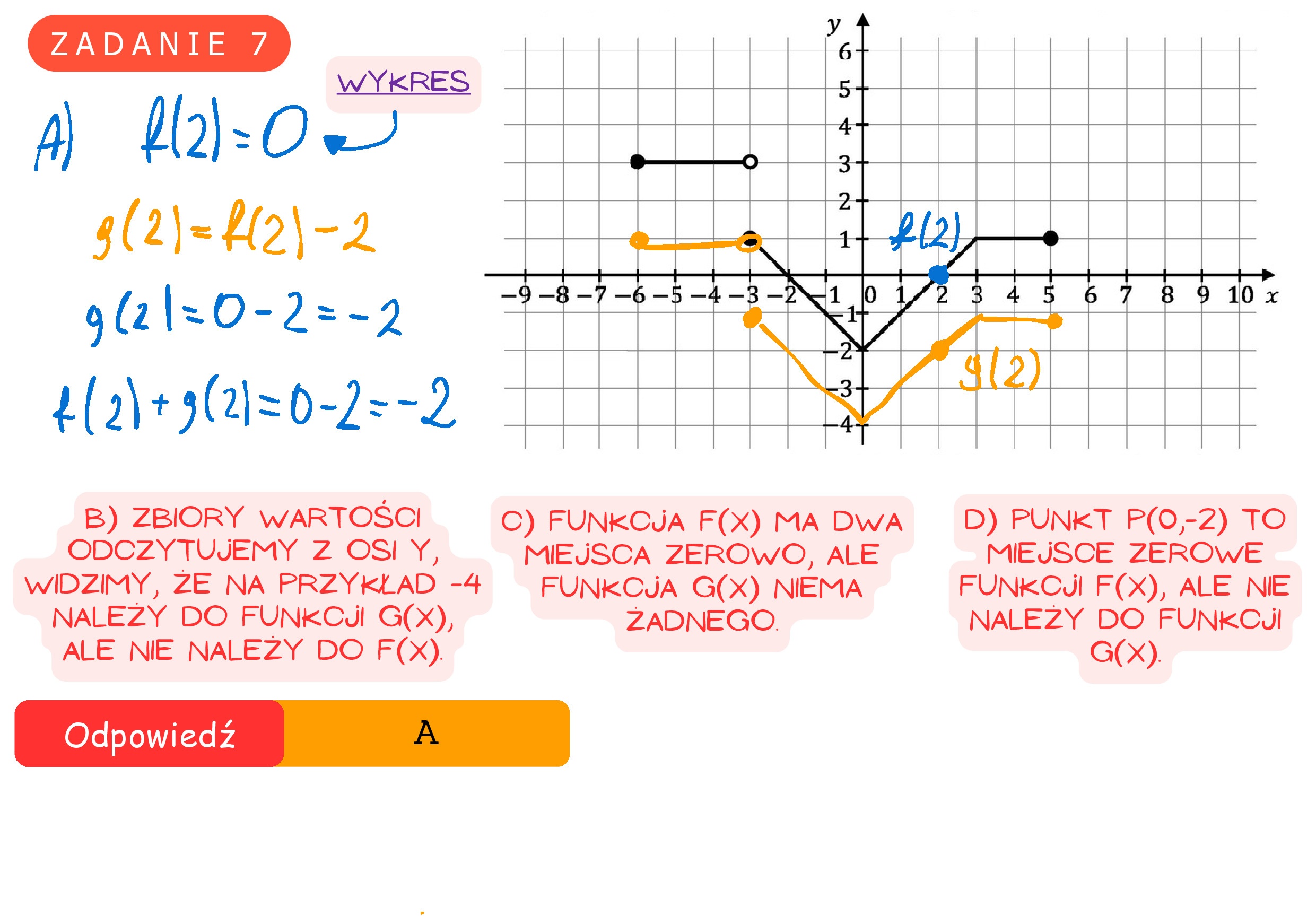
Zadanie 7. (0—1) Na poniższym rysunku przedstawiono wykres funkcji f określonej w zbiorze (—6,5). Funkcja g jest określona wzorem gf(x) =f(x)—2 dla x € (—6,5). Wskaż zdanie prawdziwe. A. Liczba f(2) + g(2) jestrówna (—2). B. Zbiory wartości funkcji f i g są równe. C. Funkcje f i g mają te same miejsca zerowe. D. Punkt P = (0, —2) należy do wykresów funkcji f i g.
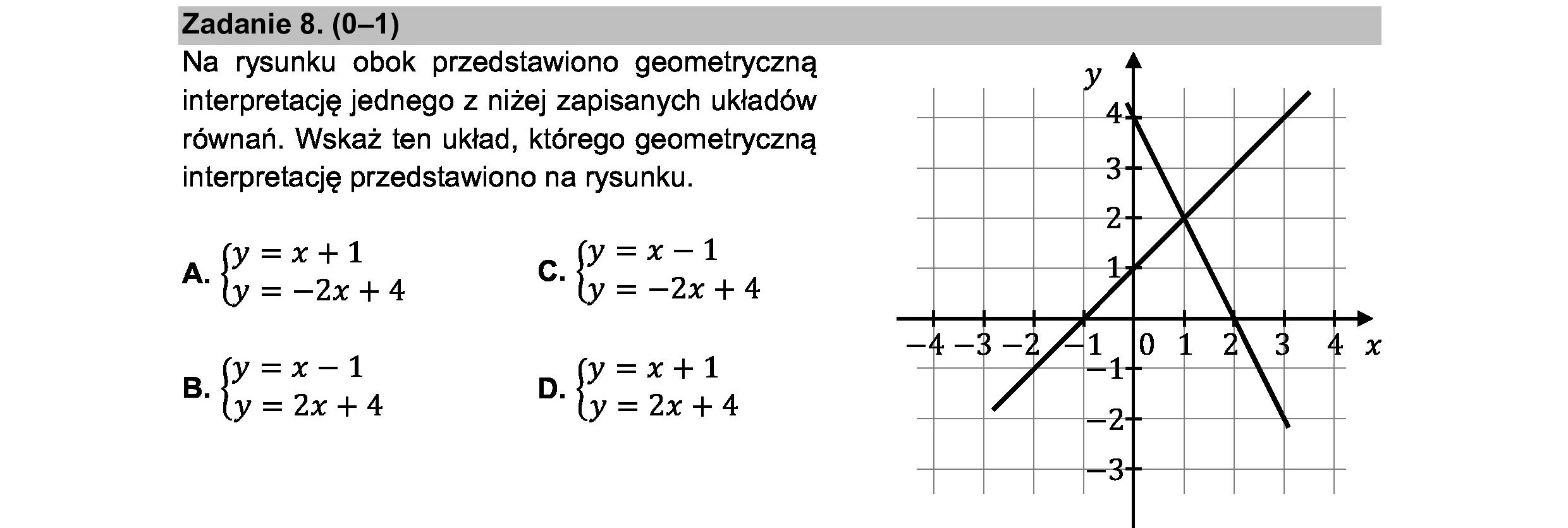
Zadanie 8. (0—1) Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań. Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku. y=x+1 y=x-1 A y= 2x4 c. - —2x +4 y=x-1 y=x+1 B= 2x4 D. = 244
Zadanie 9. (0—1) Proste o równaniach y = 3x —5 oraz y= a. ż x +z E są równoległe, gdy A.m=1 B.m=3 c m=6 D.m=9


Zadanie 10. (0—1) Funkcja f jest określona wzorem f(x) = 3 dla każdej liczby rzeczywistej x < 1. Wtedy dla argumentu x = V3 — 1 wartość mie p jest równa A. Z B. —1 c.1 D. —_ /3—1 /3—2

Zadanie 11. (0—1) Do wykresu funkcji f określonej dla każdej liczby rzeczywistej x wzorem f(x) =3*-2 należy punkt o współrzędnych A. (—1, —5) B. (0, —2) c. (0, —1) D. (2,4)


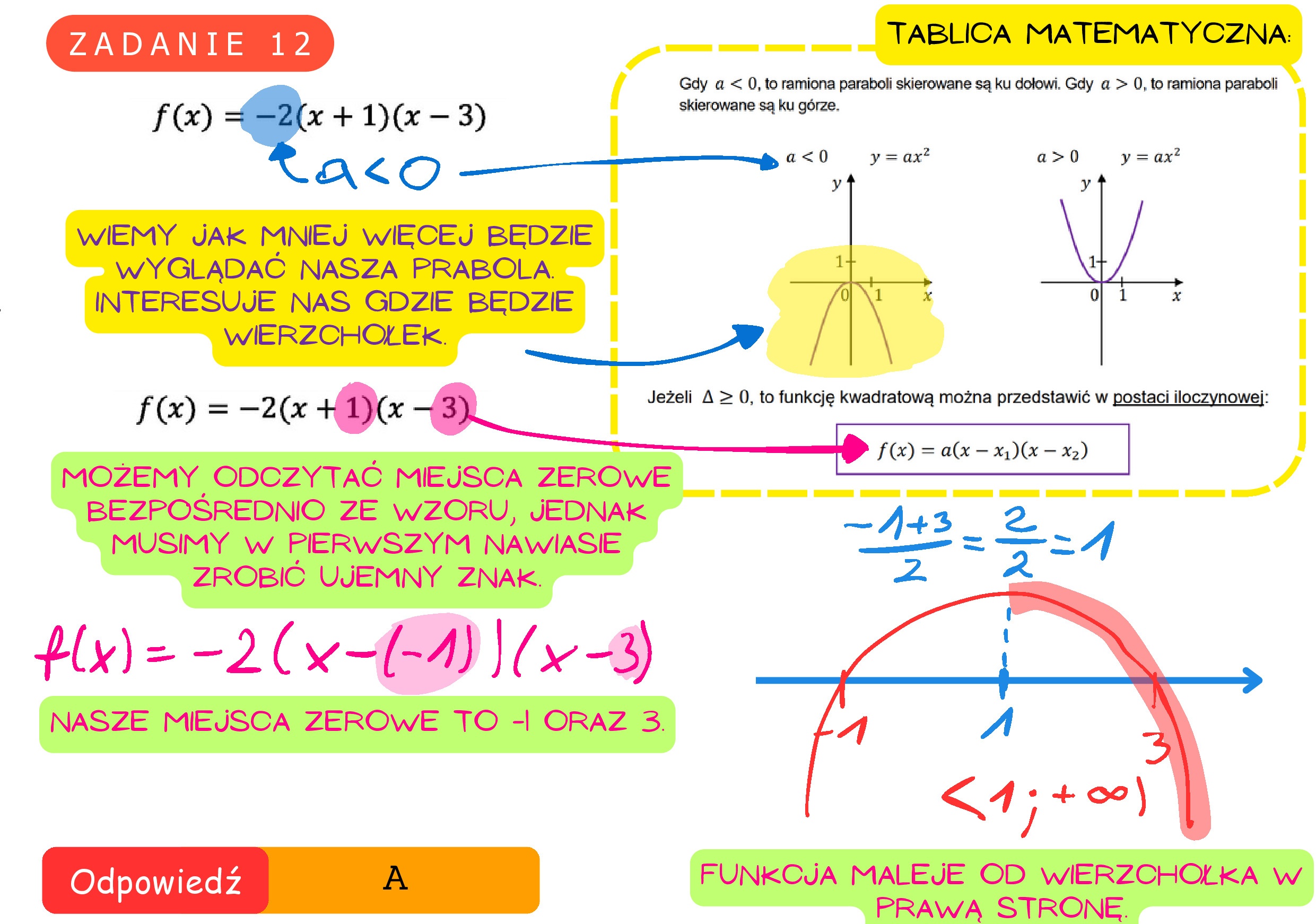
Zadanie 12. (0—1) Funkcja kwadratowa f _ określona wzorem f(x) = —2(x + 1)(x —3) jest malejąca w przedziale A. (1, +00) B. (—o, 1) C. (—0, —8) D. (—8, +00)
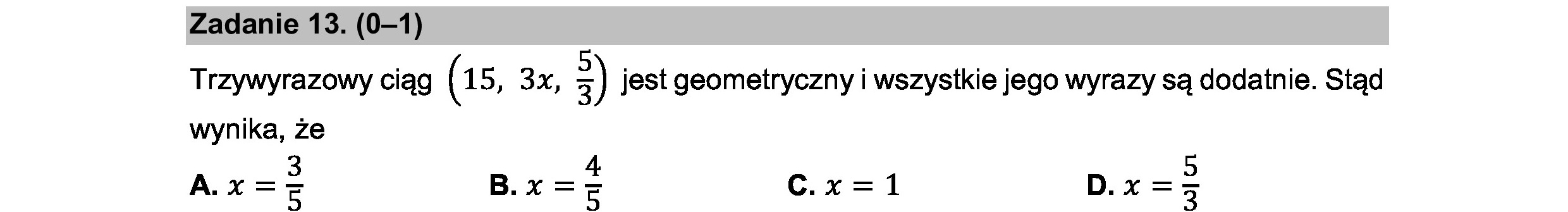
Zadanie 13. (0—1) Trzywyrazowy ciąg (15, 3x, Ą jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że 3 4 5 A.x=5 B.x=c Cc.x=1 D.x=3
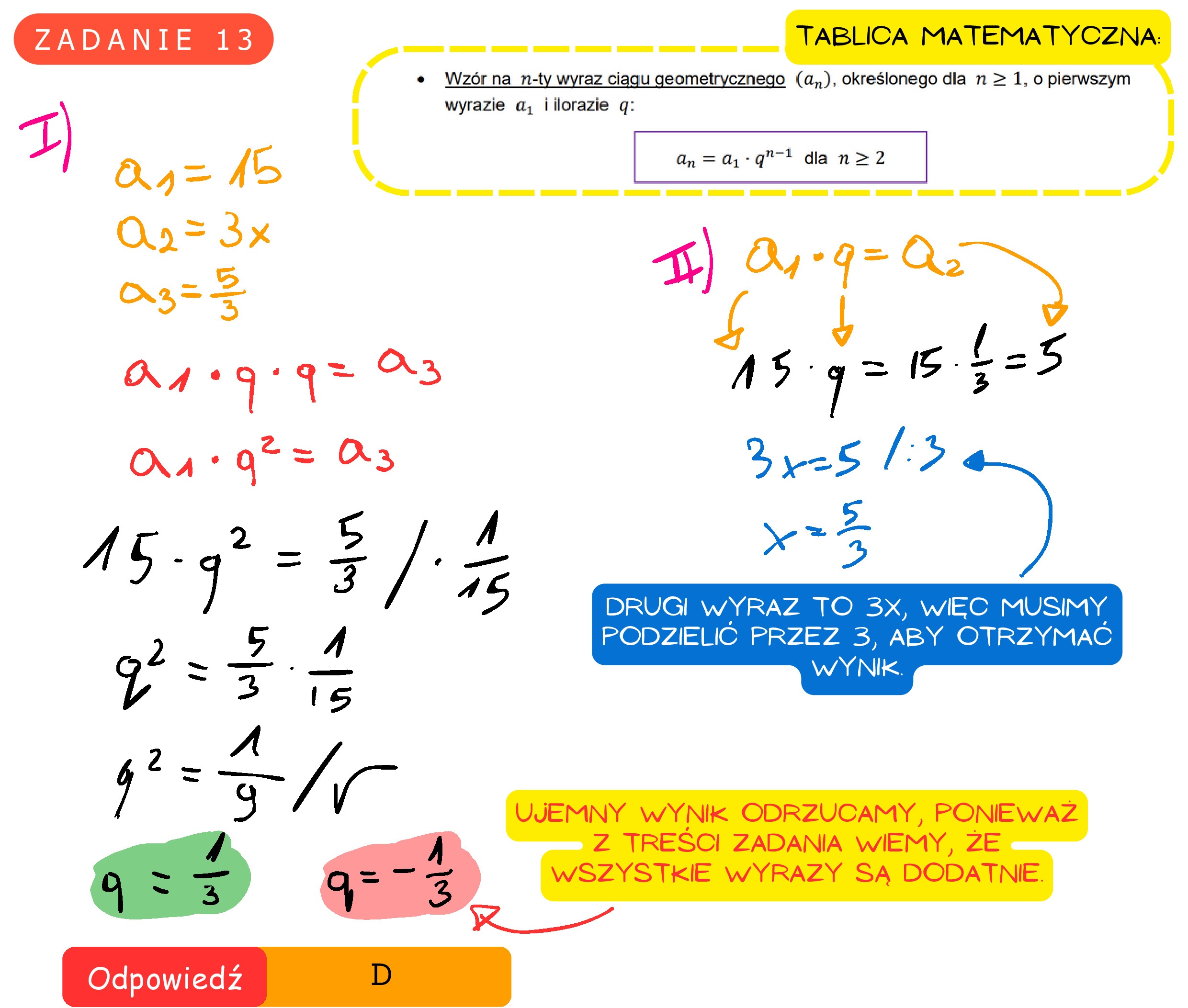

Zadanie 14. (0—1) Ciąg (b„) jest określony wzorem b, = 3n? — 25n dla każdej liczby naturalnej n > 1. Liczba niedodatnich wyrazów ciągu (b„) jest równa A. 14 B. 13 Cc. 9 D. 8

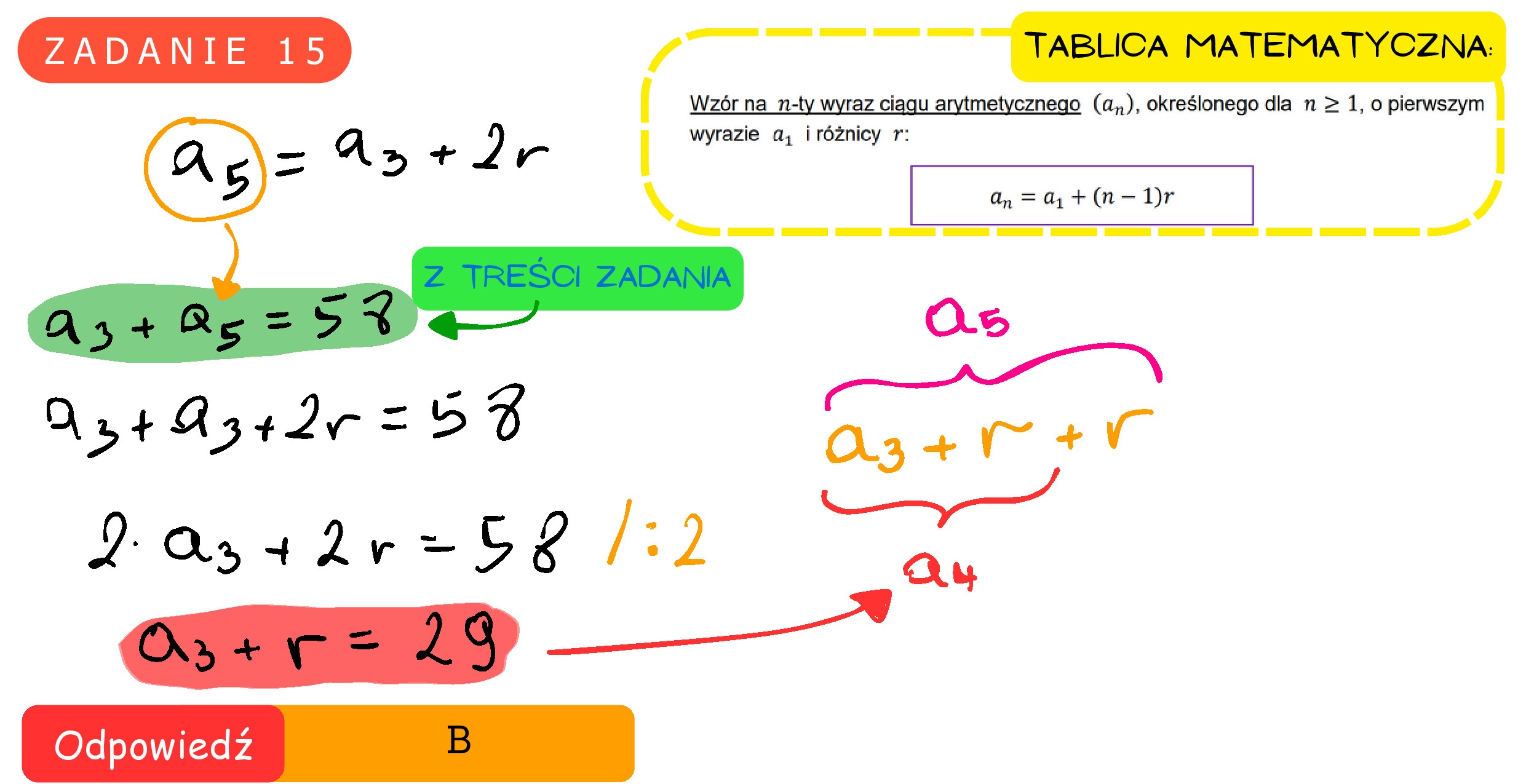
Zadanie 15. (0—1) Ciąg arytmetyczny (a) jest określony dla każdej liczby naturalnej n > 1. Trzeci i piąty wyraz ciągu spełniają warunek a; + a; = 58. Wtedy czwarty wyraz tego ciągu jest równy A. 28 B. 29 Cc. 33 D. 40
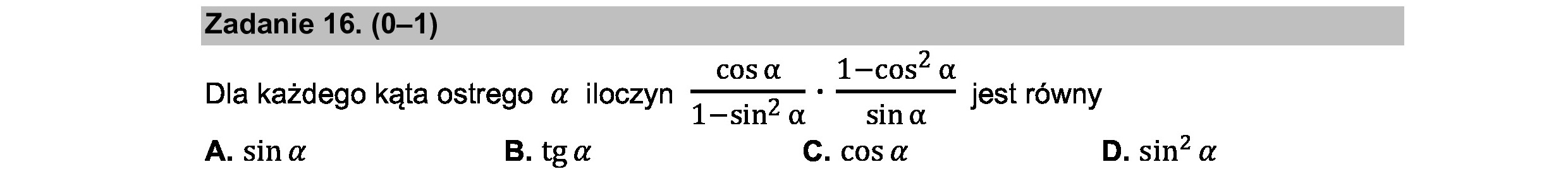
Zadanie 16. (0—1) , cos a 1-cos? a , Dla każdego kąta ostrego a iloczyn N———— * ———-- jest równy 1-sin* a sin a A. sina B. tga C. cosa D. sin? a
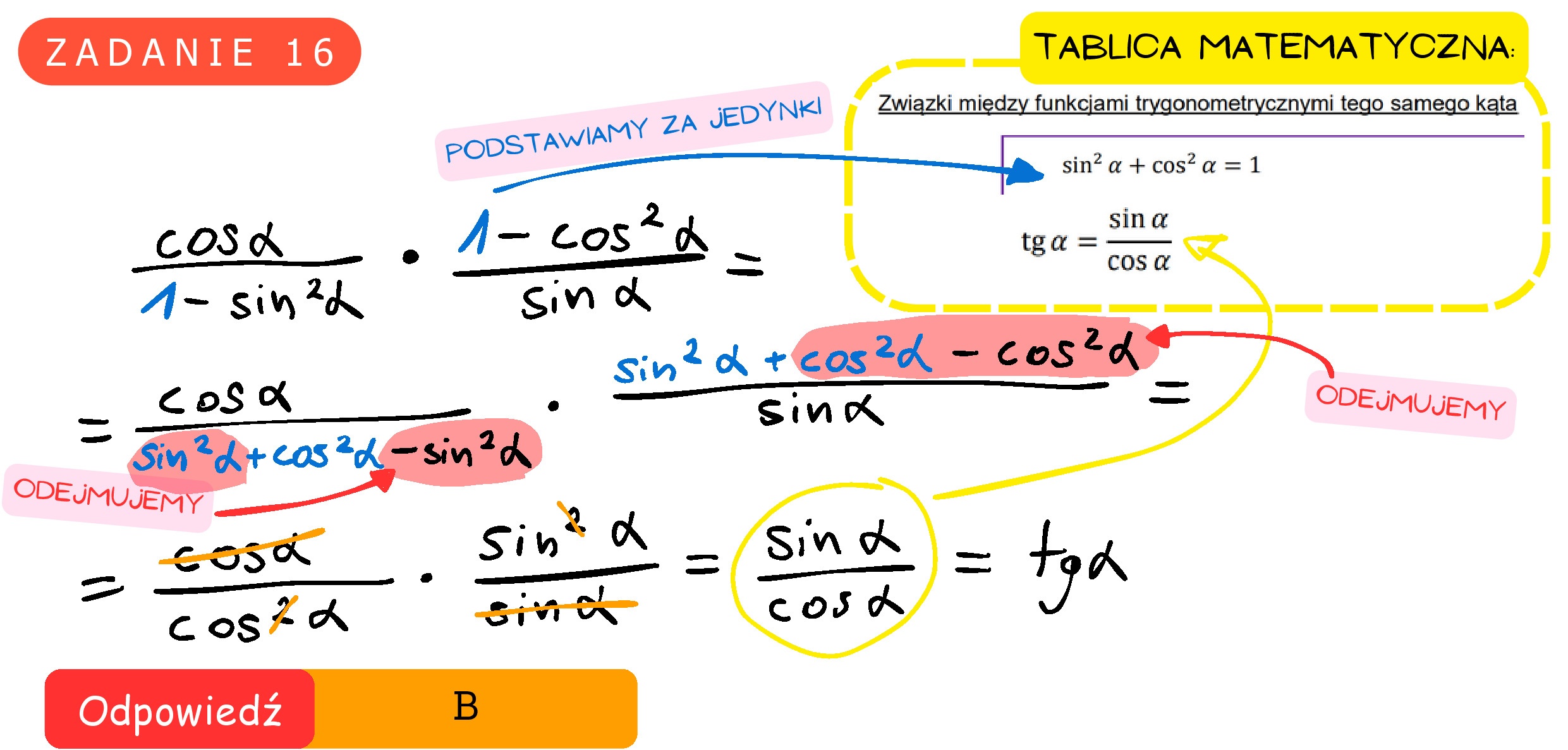
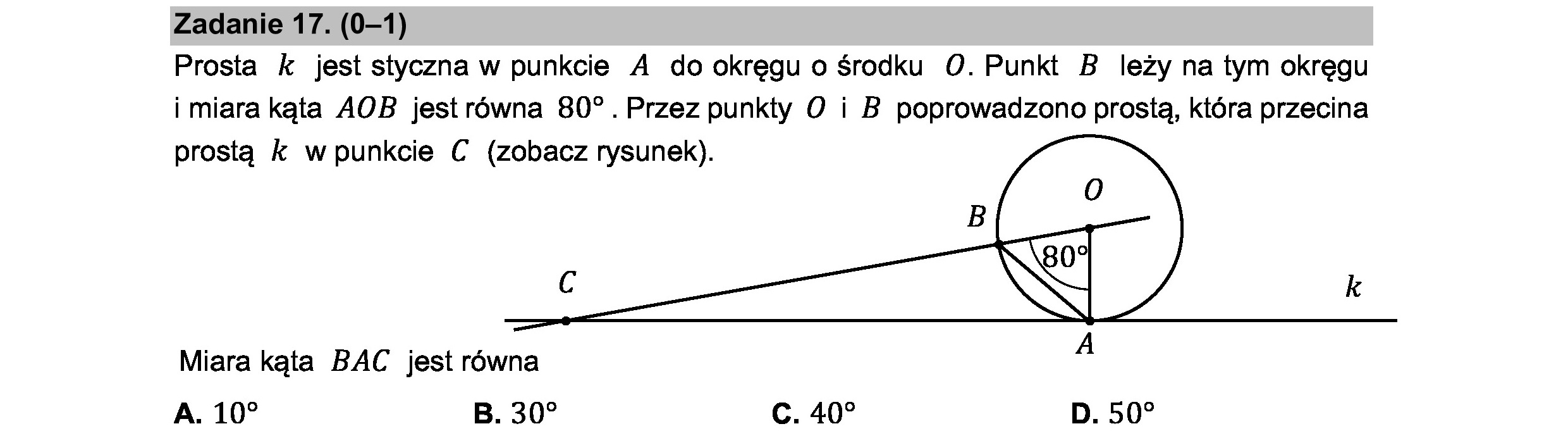
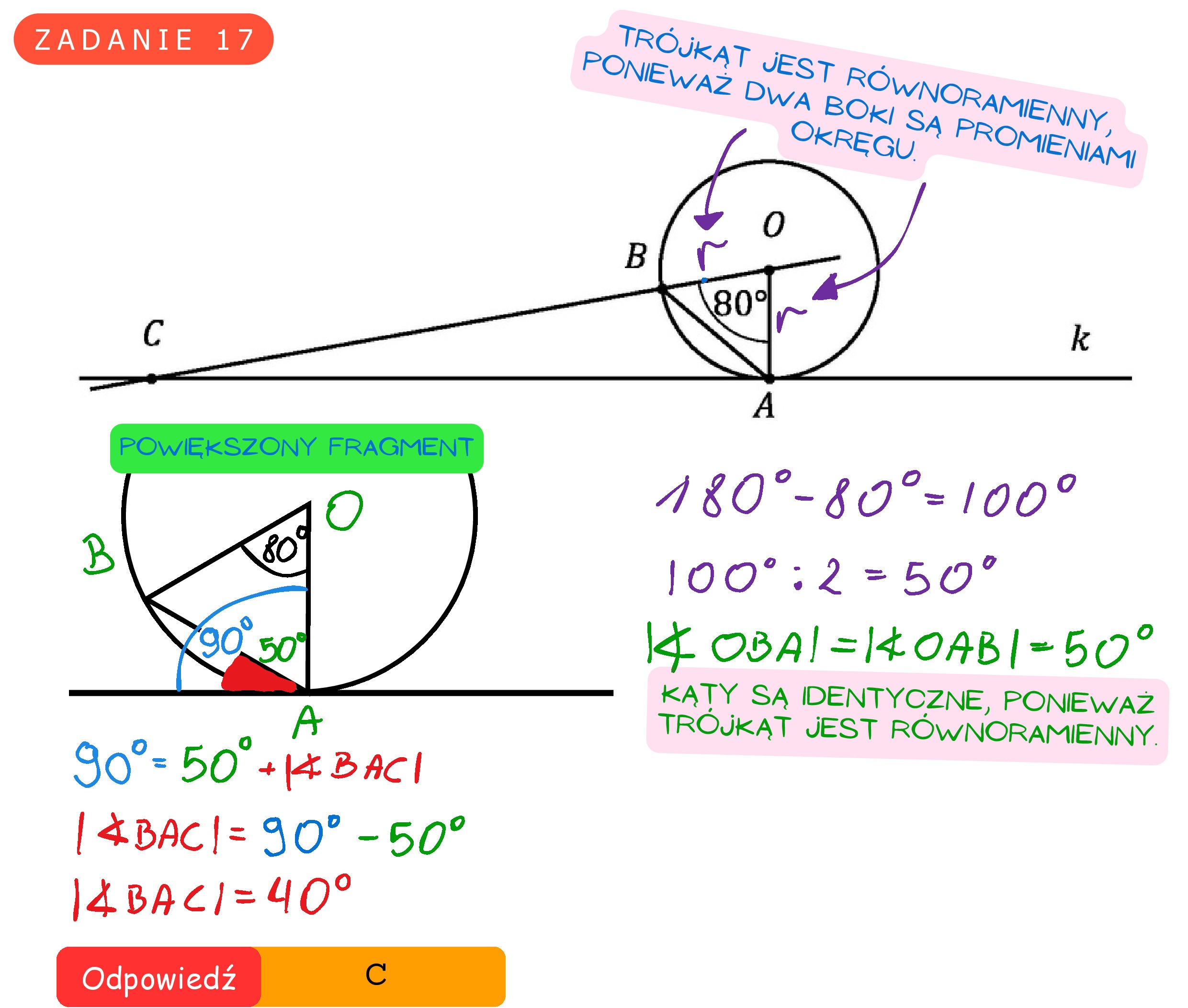
Zadanie 17. (0-1) Prosta k jest styczna w punkcie A do okręgu o środku O. Punkt B leży na tym okręgu i miara kąta AOB jest równa 80”. Przez punkty O i B poprowadzono prostą, która przecina prostą k w punkcie C (zobacz rysunek). Miara kąta BAC jest równa A A. 10? B. 30? c. 407 D. 50?
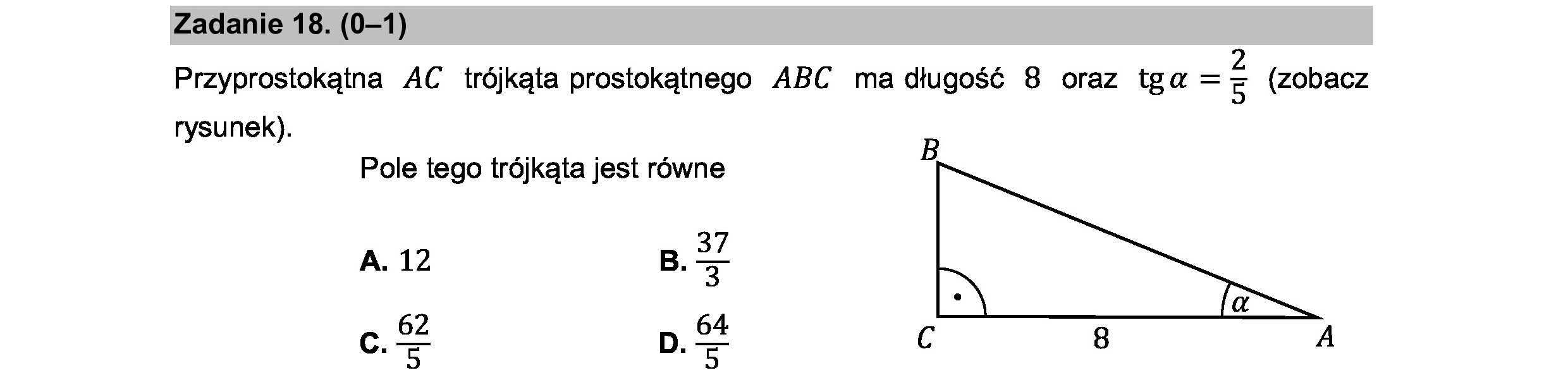
Zadanie 18. (0—1) Przyprostokątna AC trójkąta prostokątnego ABC ma długość 8 oraz tga =g (zobacz rysunek). Pole tego trójkąta jest równe B A. 12 B. kc 62 64 Bi c. Ka D. 5 C 8 A
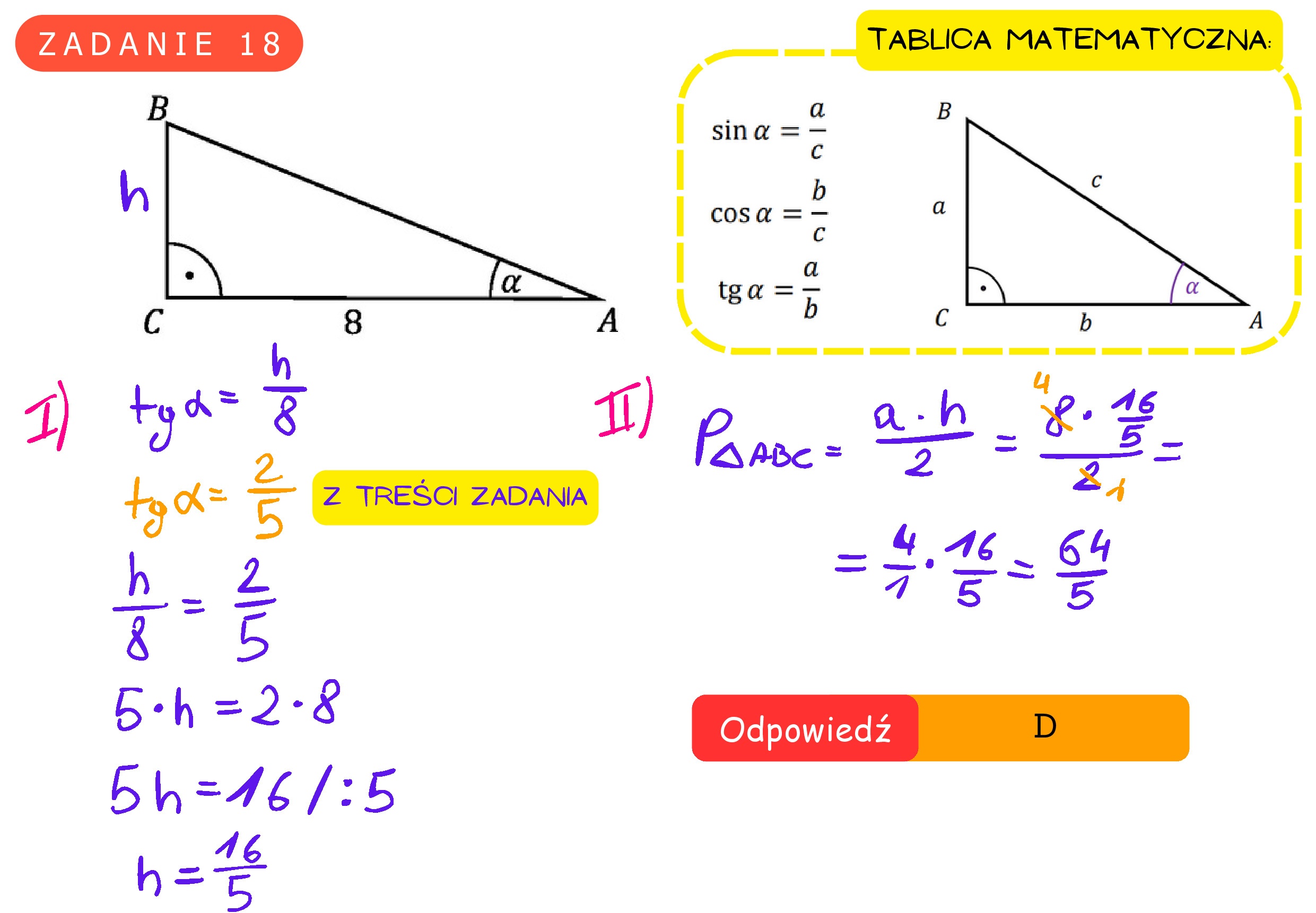

Zadanie 19. (0-1) Pole pewnego trójkąta równobocznego jest równe SE) Obwód tego trójkąta jest równy 4 2 A. 4 B. 2 C.z D. z

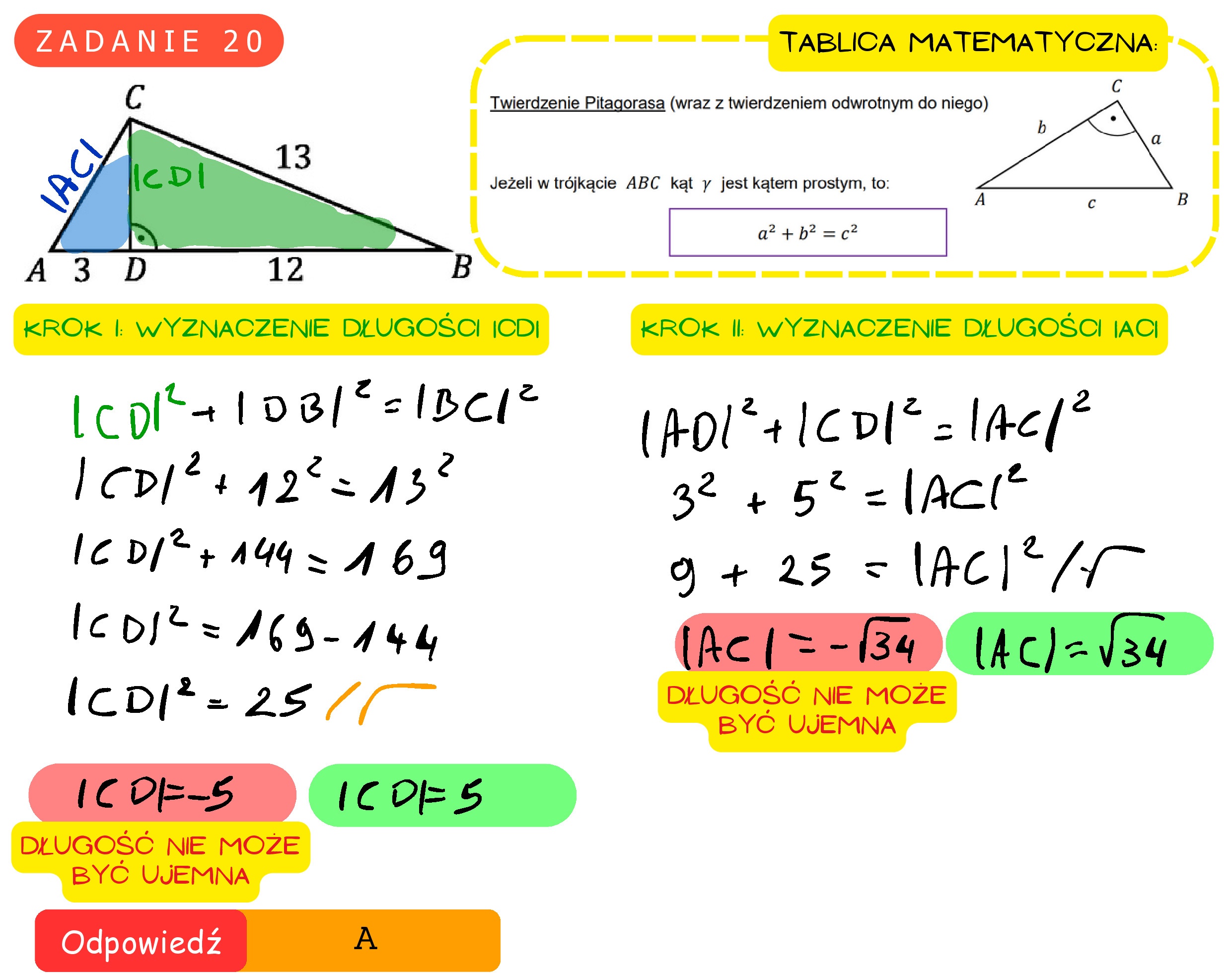
Zadanie 20. (0—1) W trójkącie ABC bok BC madługość 13, a wysokość CD tego trójkąta dzieli bok AB na odcinki o długościach |AD| = 3 i |BD| = 12 (zobacz rysunek obok). Długość boku AC jest równa A. Vv34 B. > C. 2v14 3 13 12 D. 3V45
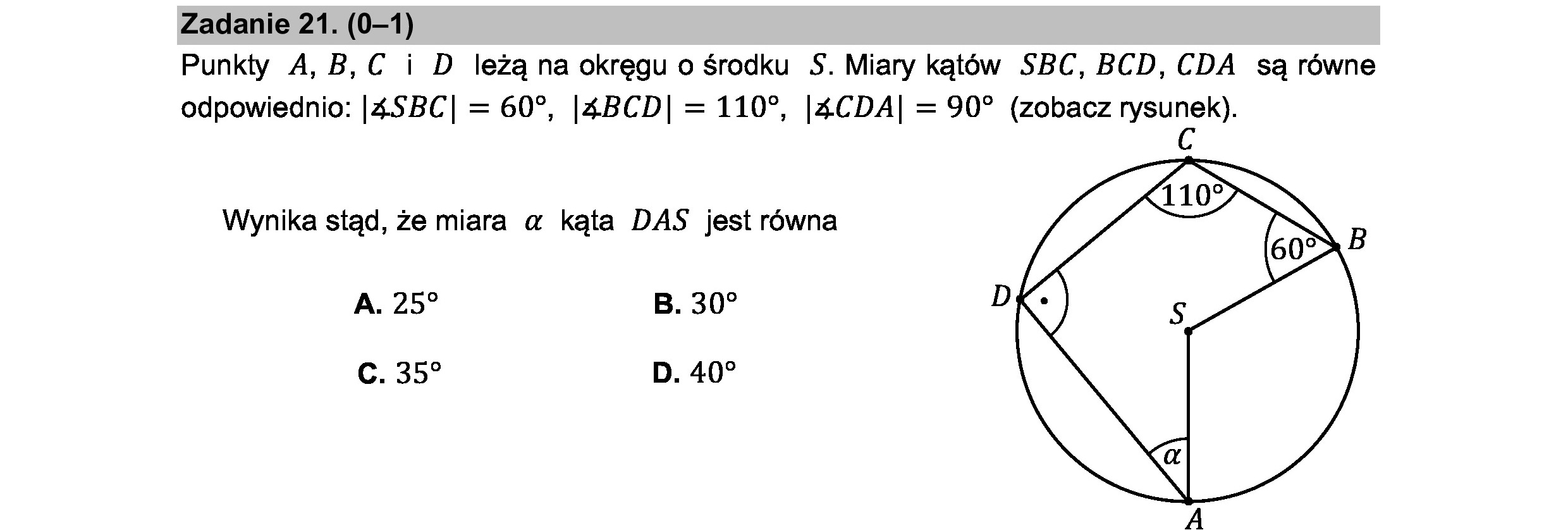
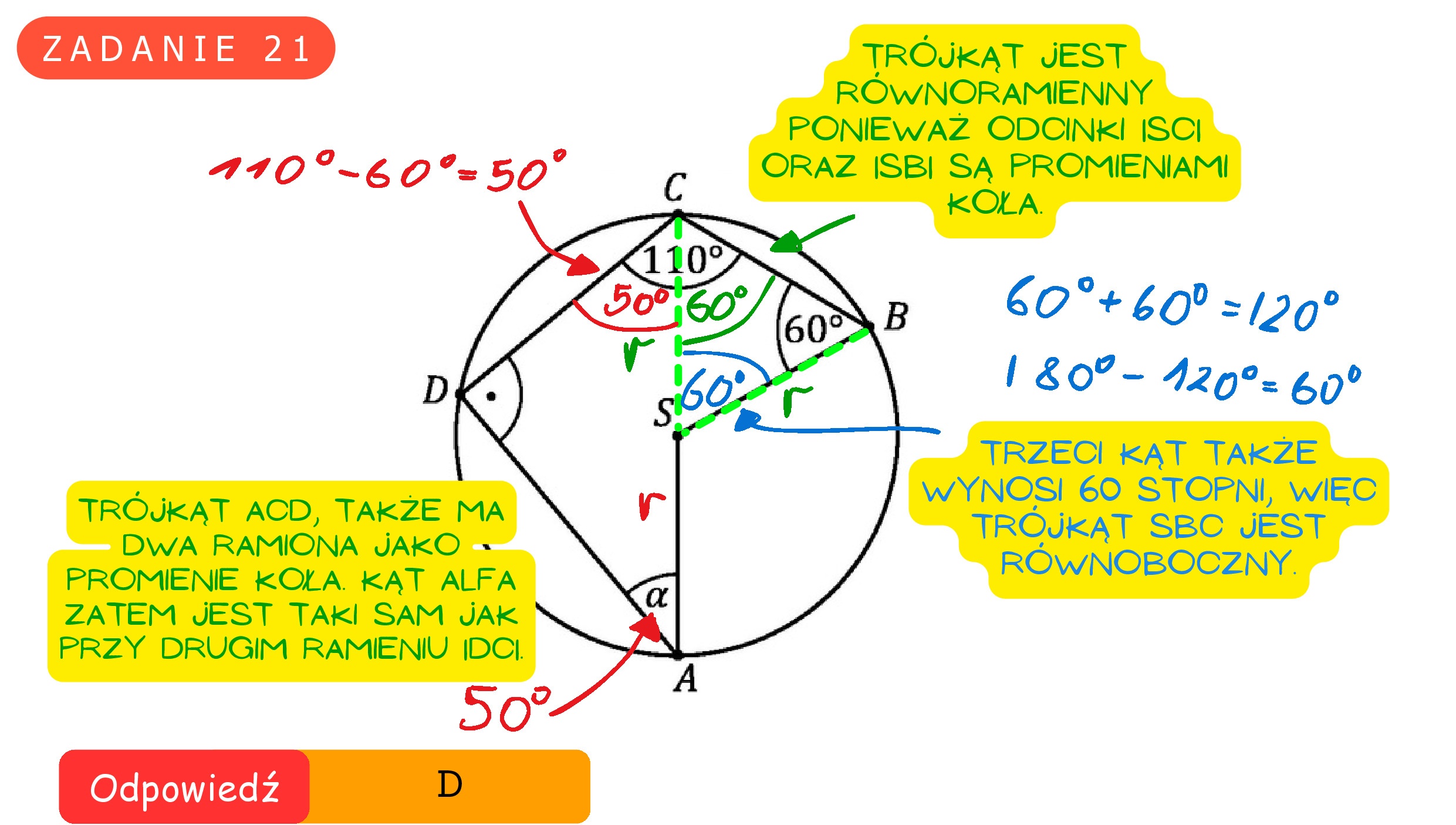
Zadanie 21. (0—1) Punkty A,B,C i D leżą na okręgu o środku S. Miary kątów SBC, BCD, CDA są równe odpowiednio: |4SBC| = 60”, |4BCD| = 110%, |4CDA| = 90? (zobacz rysunek). C Wynika stąd, że miara a kąta DAS jest równa >» B A. 259 B. 307 D c) c. 35? D. 40? Ś
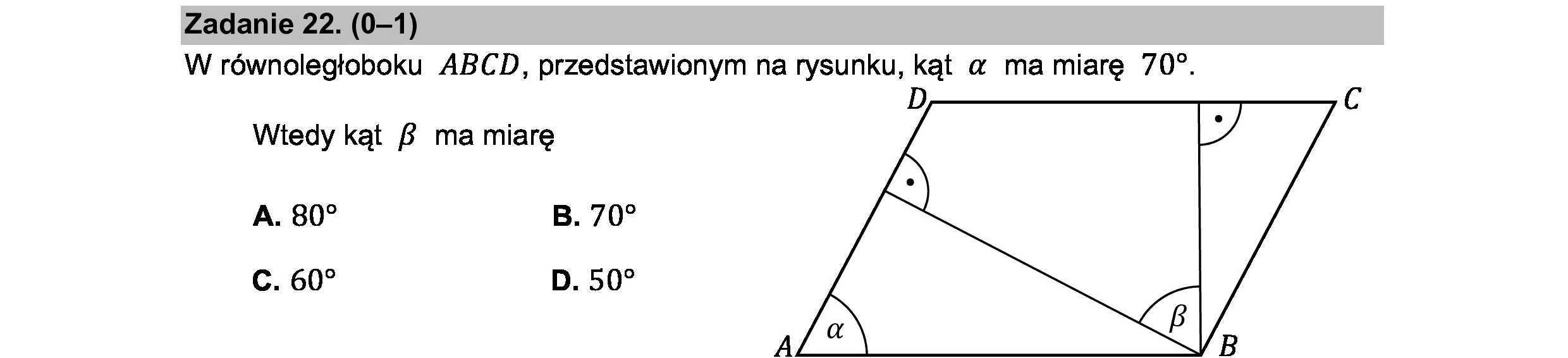
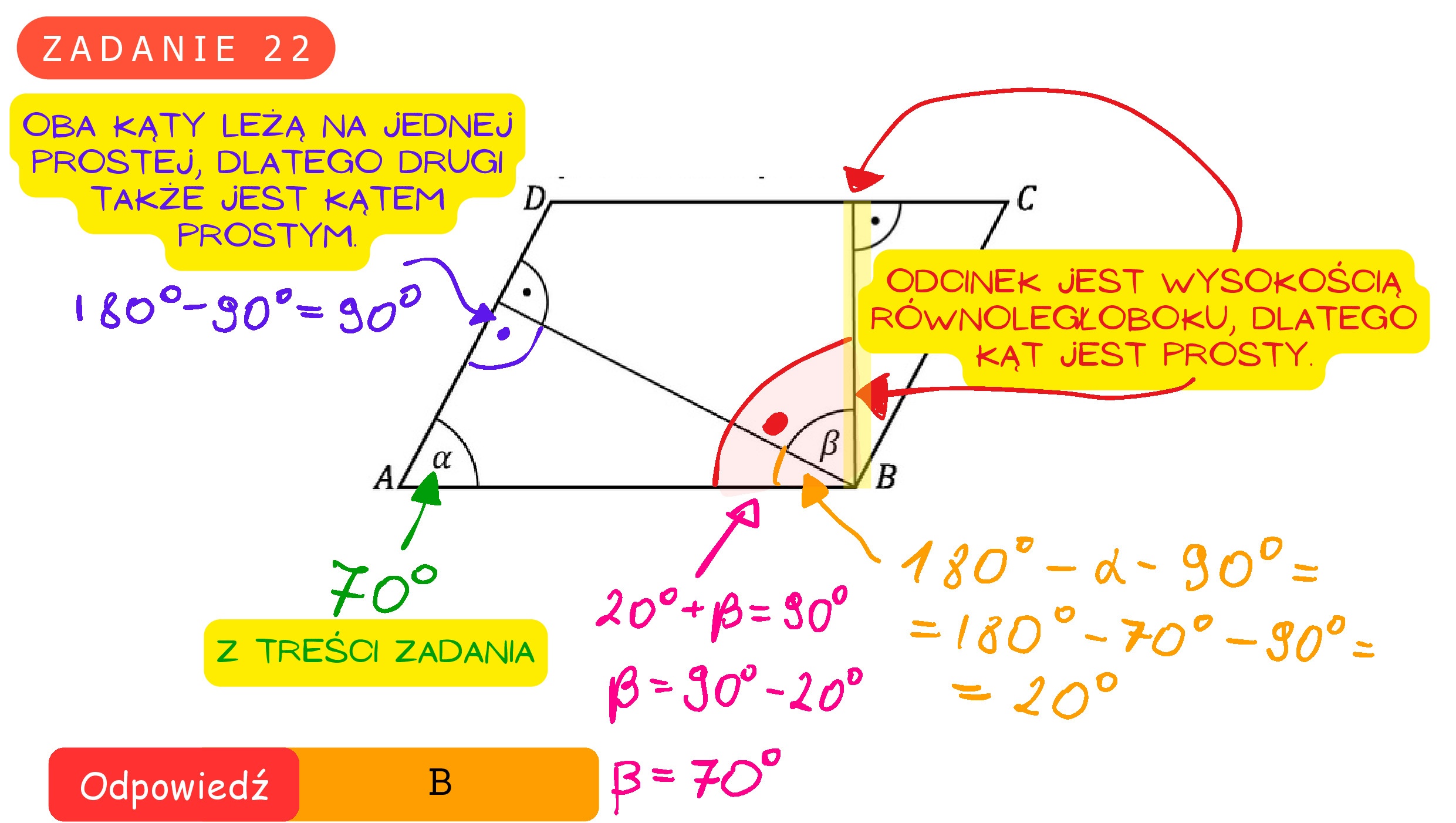
Zadanie 22. (0—1) W równoległoboku ABCD, przedstawionym na rysunku, kąt a ma miarę 709. Wtedy kąt 8 ma miarę A. 80? B. 70? c. 60? D. 507

Zadanie 23. (0-1) W każdym n-kącie wypukłym (n > 3) liczba przekątnych jest równa 203) . Wielokątem wypukłym, w którym liczba przekątnych jesto 25 większa od liczby boków, jest A. siedmiokąt. B. dziesięciokąt. C. dwunastokąt. D. piętnastokąt.

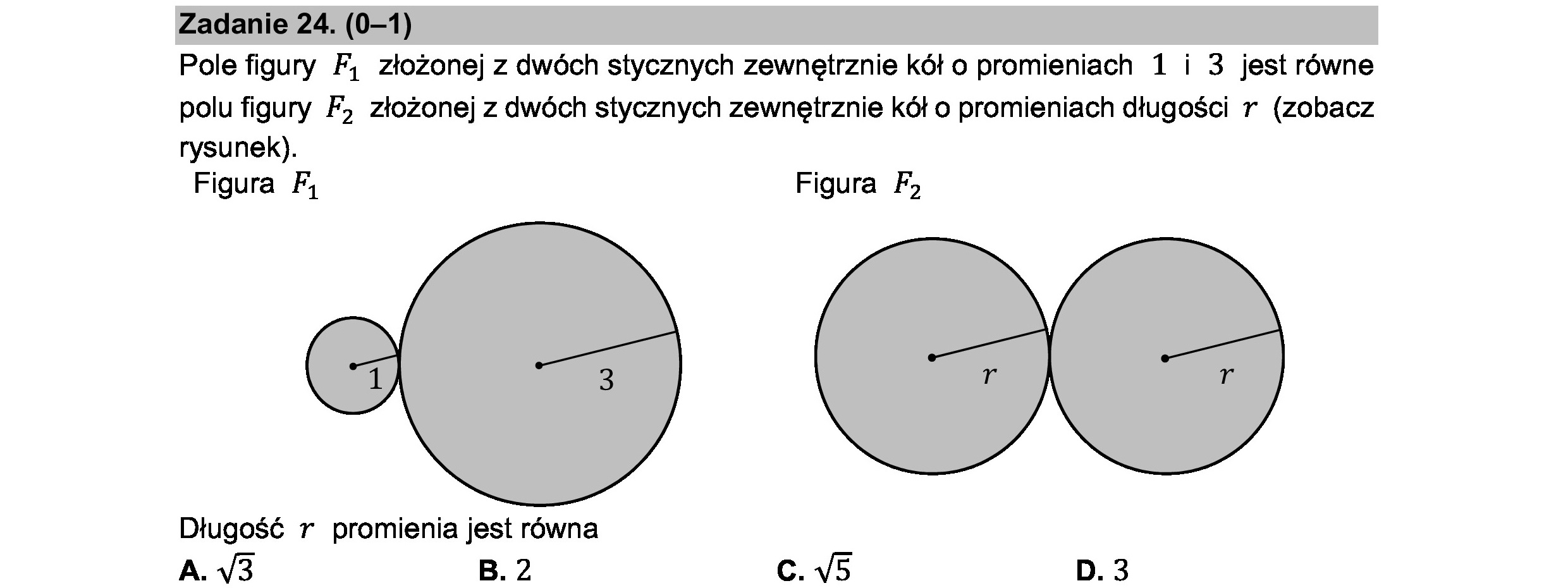
Zadanie 24. (0—1) Pole figury Fi złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury F, złożonej z dwóch stycznych zewnętrznie kół o promieniach długości r (zobacz rysunek). Figura Fi Figura F> Długość r promienia jest równa A. 43 B. 2 c. V5 D. 3
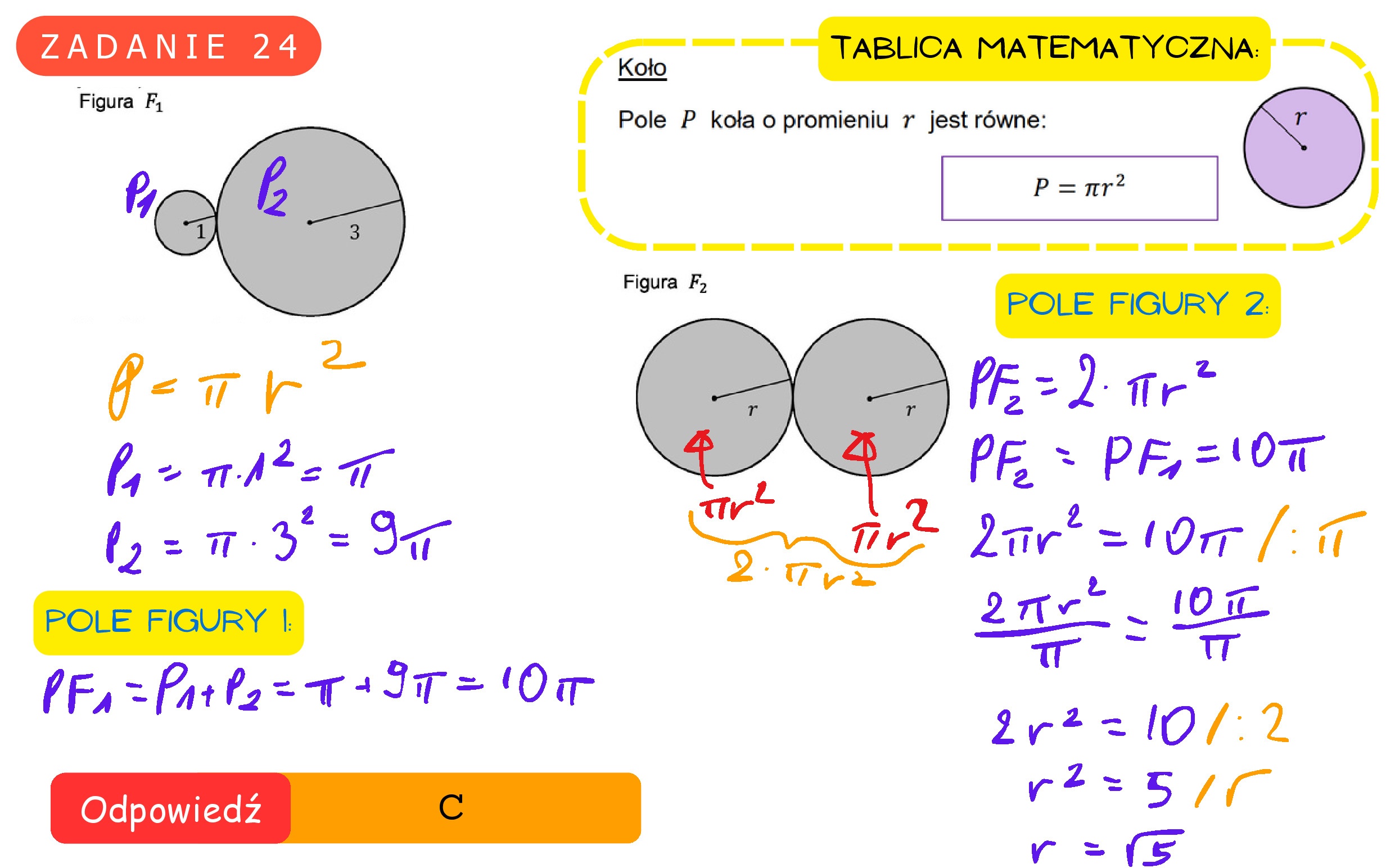

Zadanie 25. (0-1) Punkt A = (3, —5) jest wierzchołkiem kwadratu ABCD, a punkt M = (1,3) jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu ABCD jest równe A. 68 B. 136 c. 2V34 D. 8V34

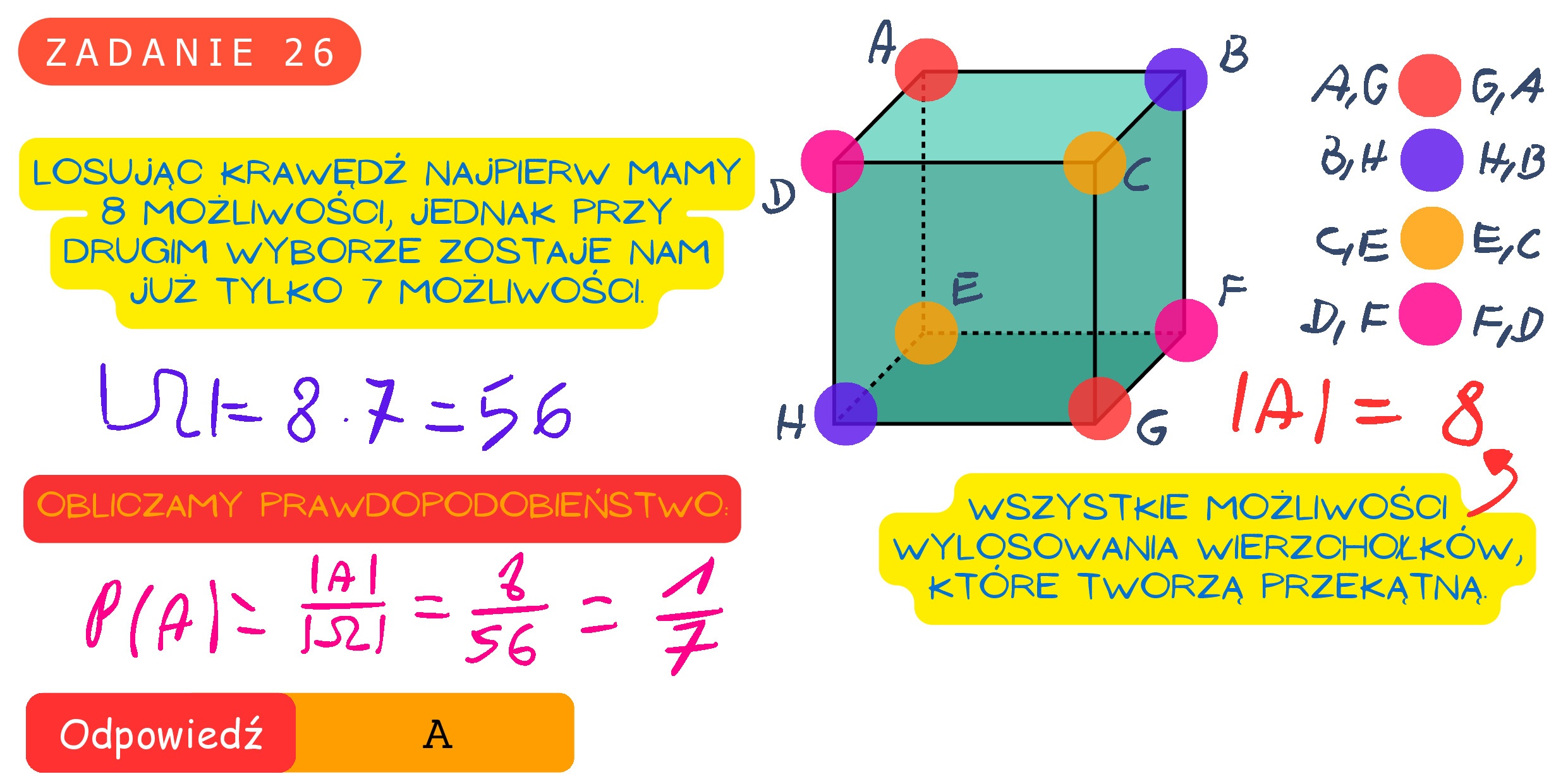
Zadanie 26. (0—1) Z wierzchołków sześcianu ABCDEFGH losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu ABCDEFGH, jest równe 1 4 1 A. 7 B. 7 C. 74 U IW

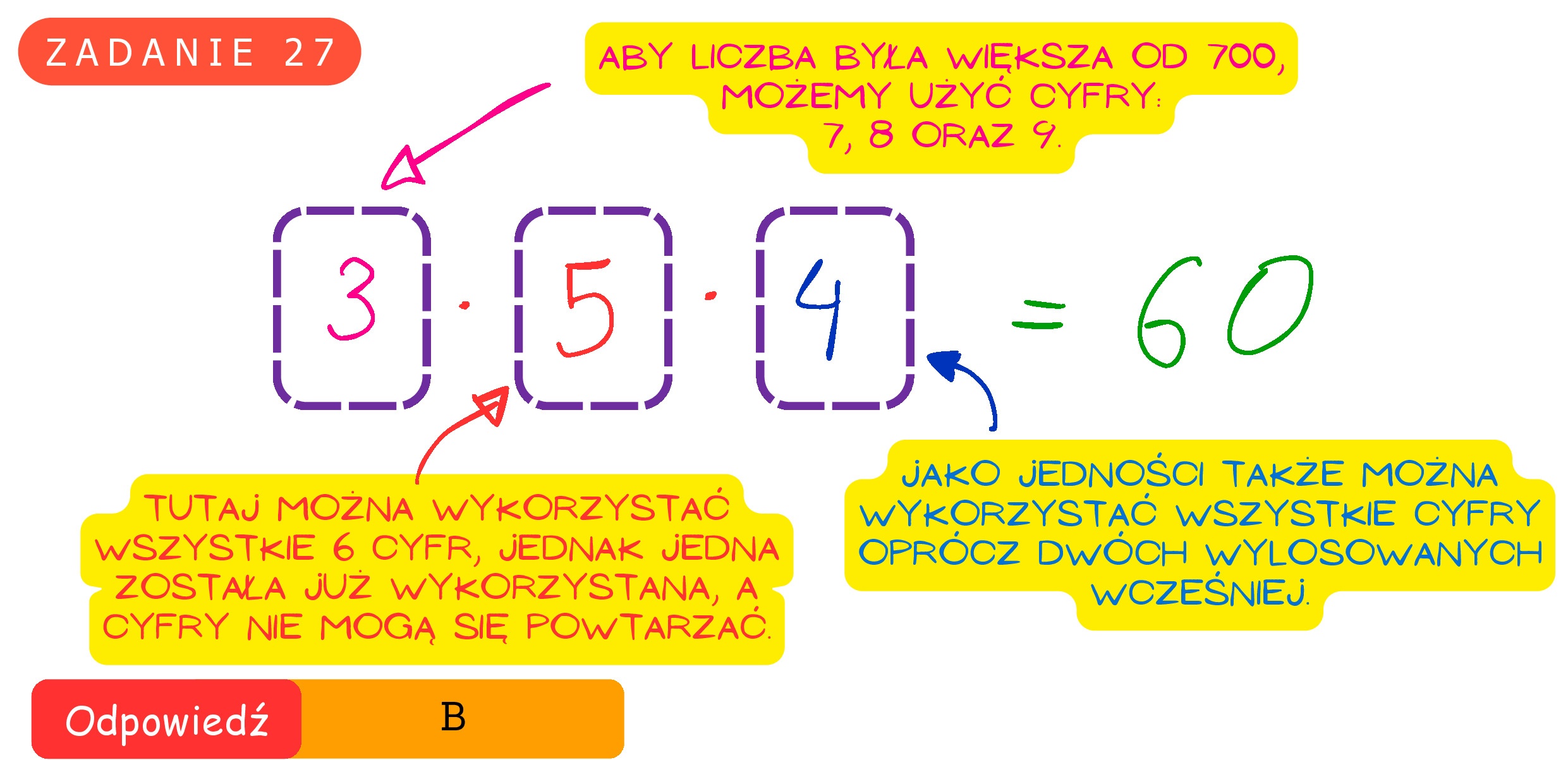
Zadanie 27. (0—1) Wszystkich liczb naturalnych trzycyfrowych, większych od 700, w których każda cyfra należy do zbioru f1,2,3,7,8,9) i żadna cyfra się nie powtarza, jest A. 108 B. 60 Cc. 40 D. 299
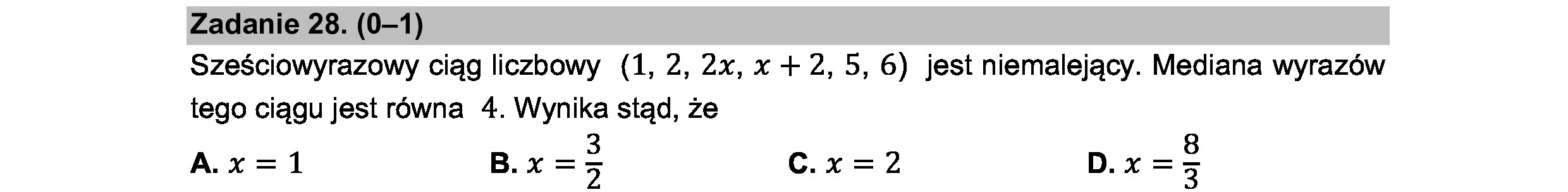
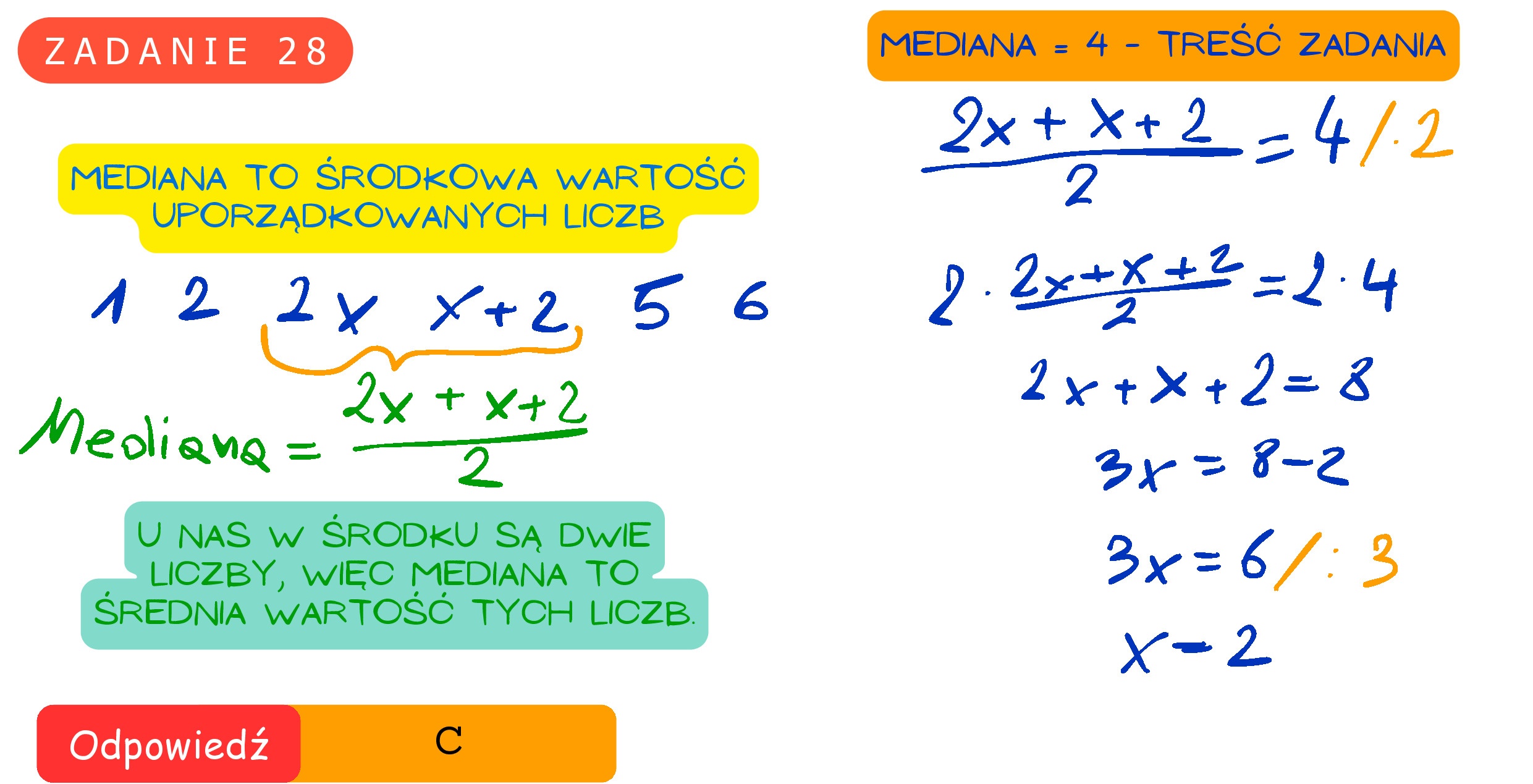
Zadanie 28. (0—1) Sześciowyrazowy ciąg liczbowy (1, 2, 2x, x + 2, 5, 6) jest niemalejący. Mediana wyrazów tego ciągu jest równa 4. Wynika stąd, że 3 8 A.x=1 B.x => C.x=2 D.x=3
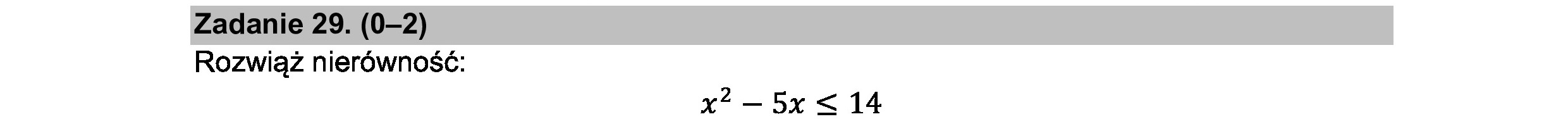
Zadanie 29. (0—2) Rozwiąż nierówność: x? —5x<14
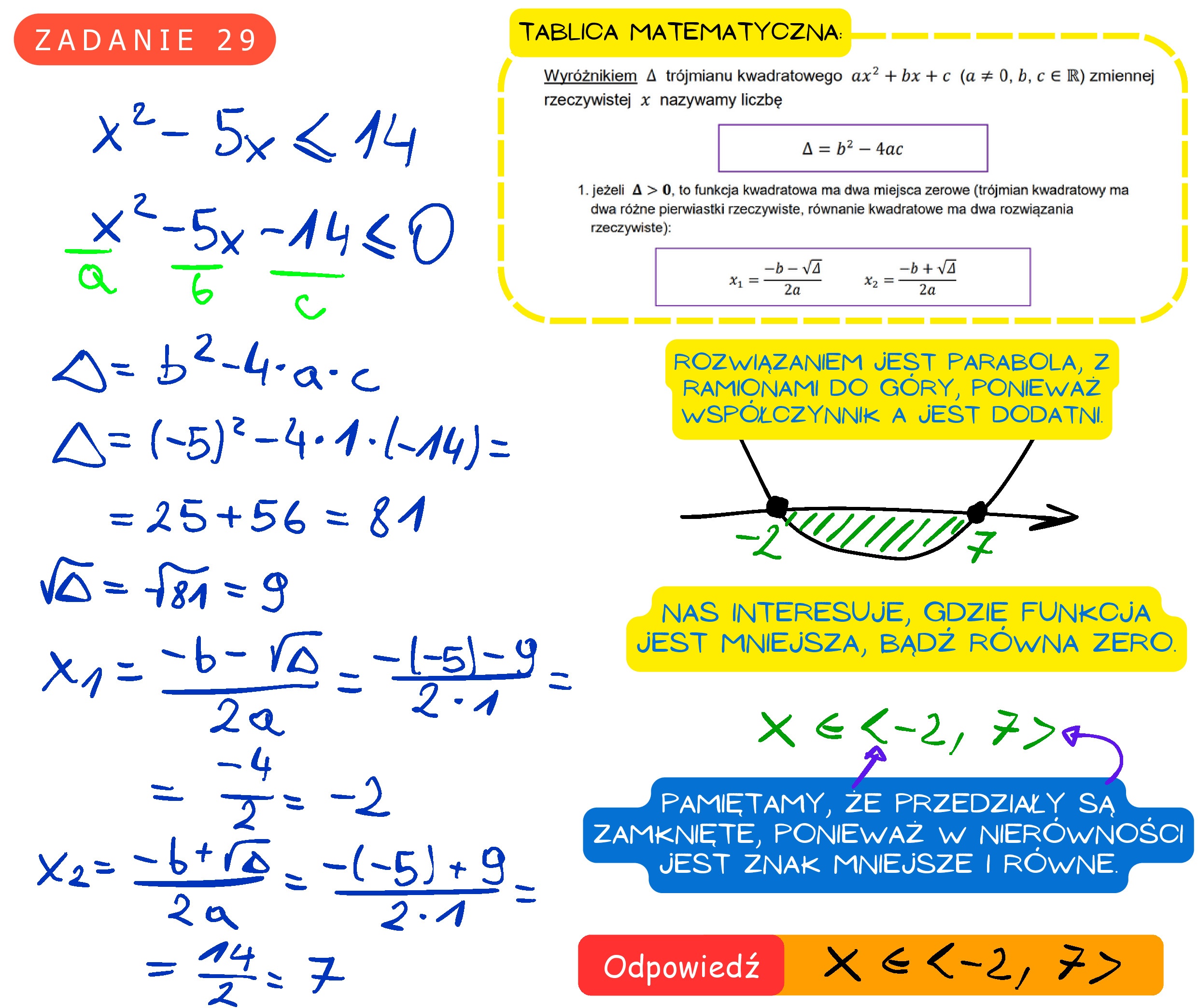
Zadanie 30. (0—2)
Wykaż, że dla każdych trzech dodatnich liczb a, b i c takich, że a 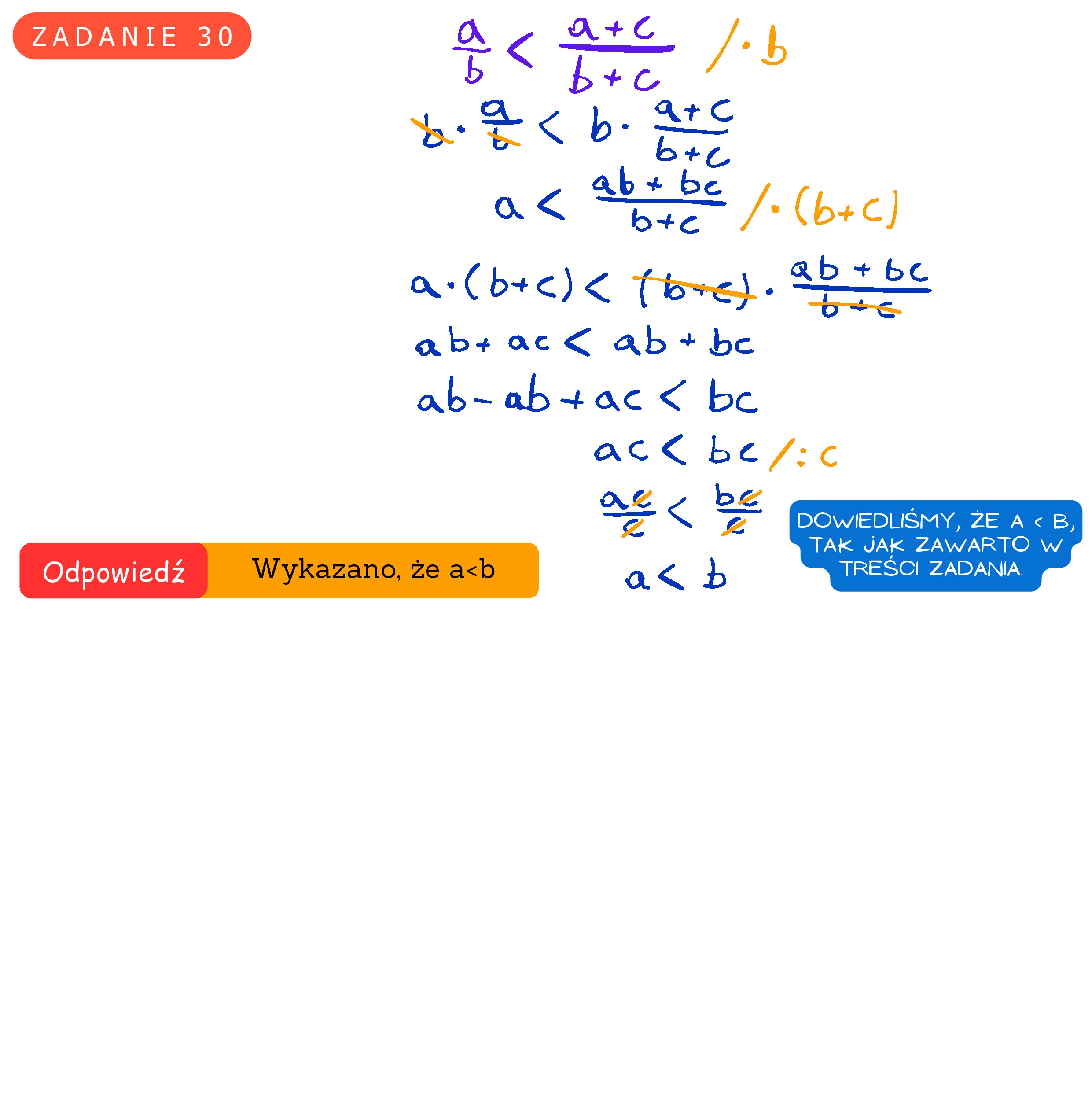

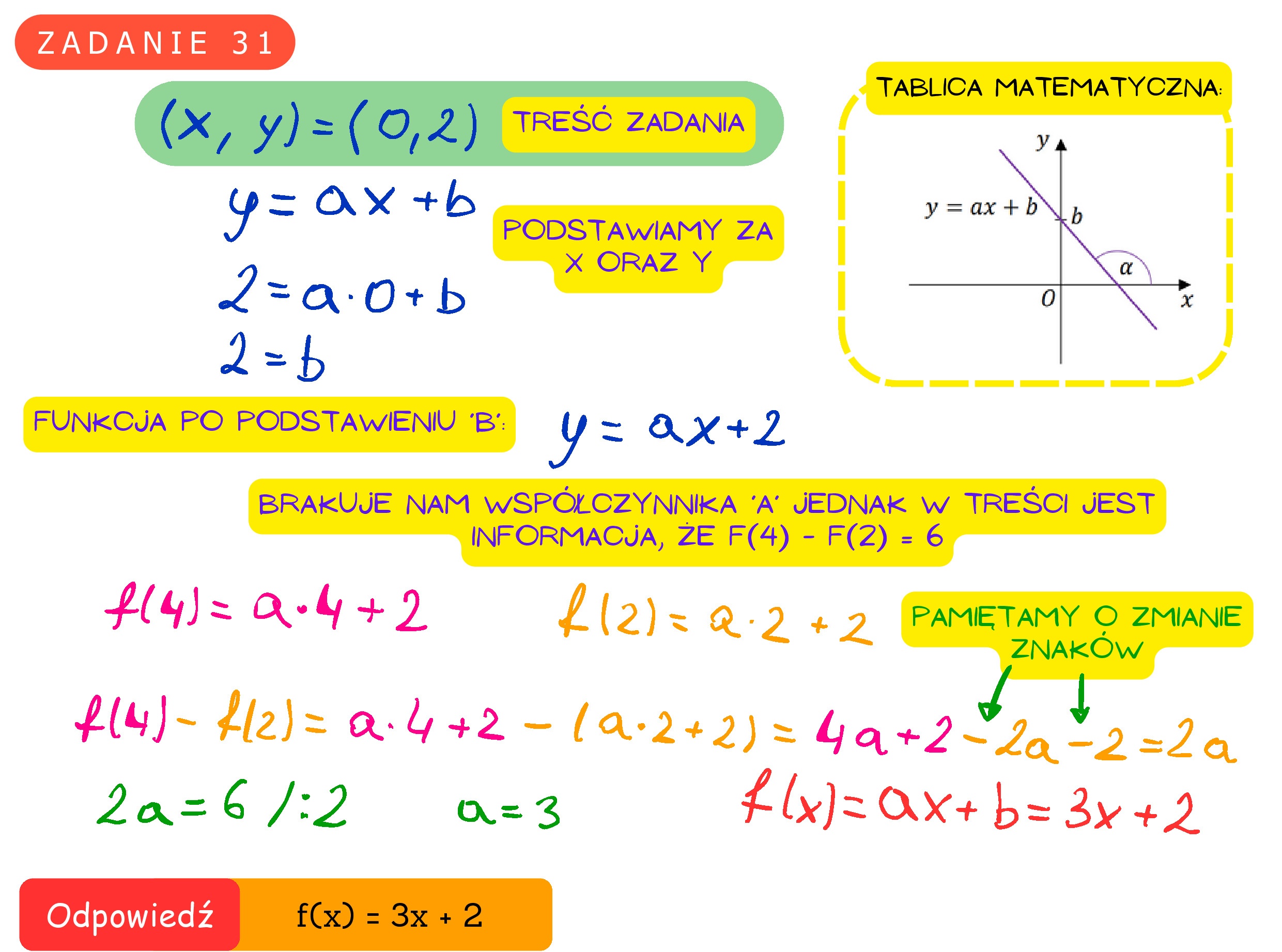
Zadanie 31. (0—2) Funkcja liniowa f przyjmuje wartość 2 dla argumentu 0, a ponadto f(4) — f(2) =6. Wyznacz wzór funkcji f.
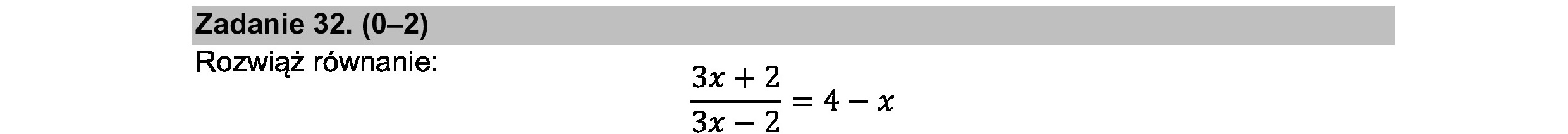
Zadanie 32. (0—2) Rozwiąż równanie: 3x +2 _ 3x—2


Zadanie 33. (0—2) Trójkąt równoboczny ABC ma pole równe 9V3. Prosta równoległa do boku BC przecina boki AB i AC — odpowiednio — w punktach K i L. Trójkąty ABC i AKL są podobne, a stosunek długości boków tych trójkątów jest równy E . Oblicz długość boku trójkąta AKL.


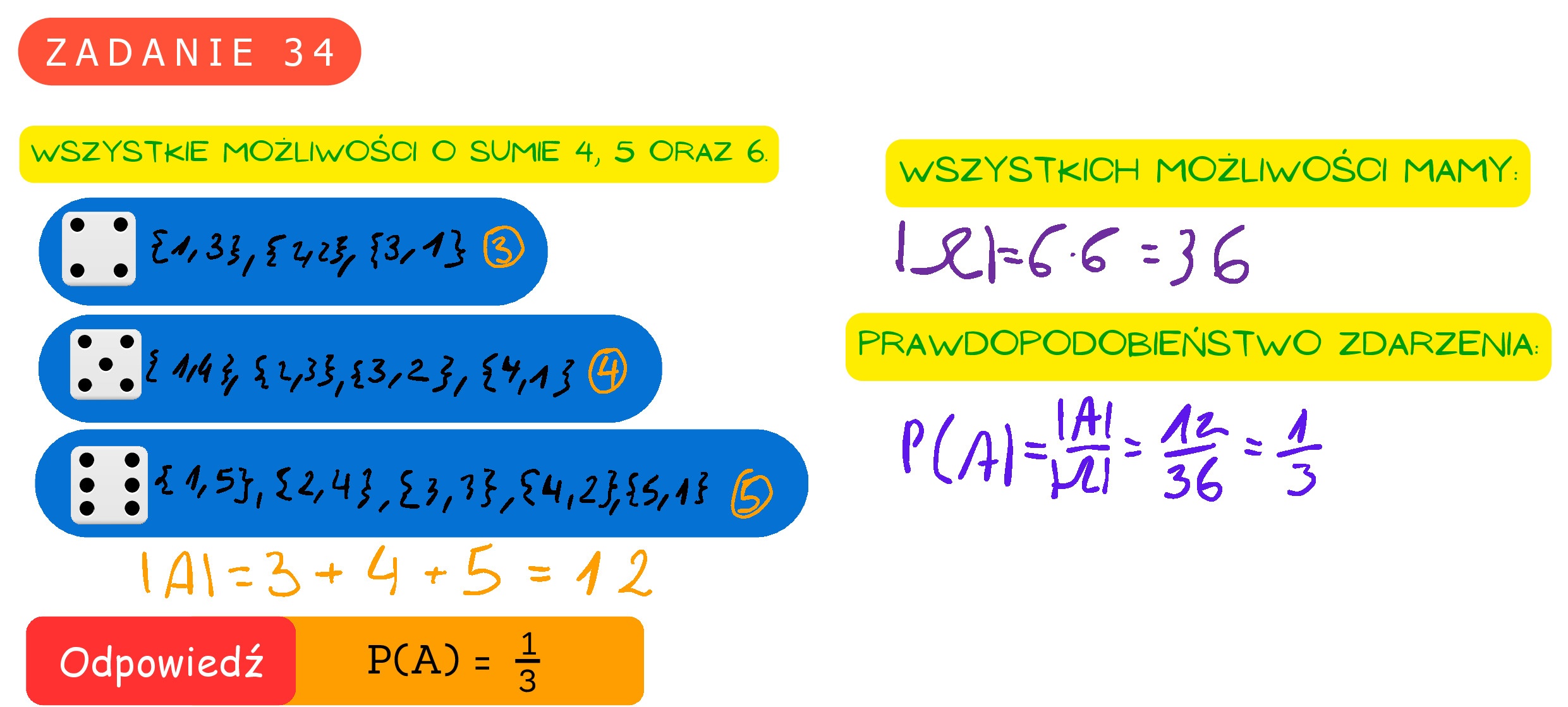
Zadanie 34. (0—2) Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza sumę liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że suma liczb wyrzuconych oczek jest równa 4 lub 5, lub 6.

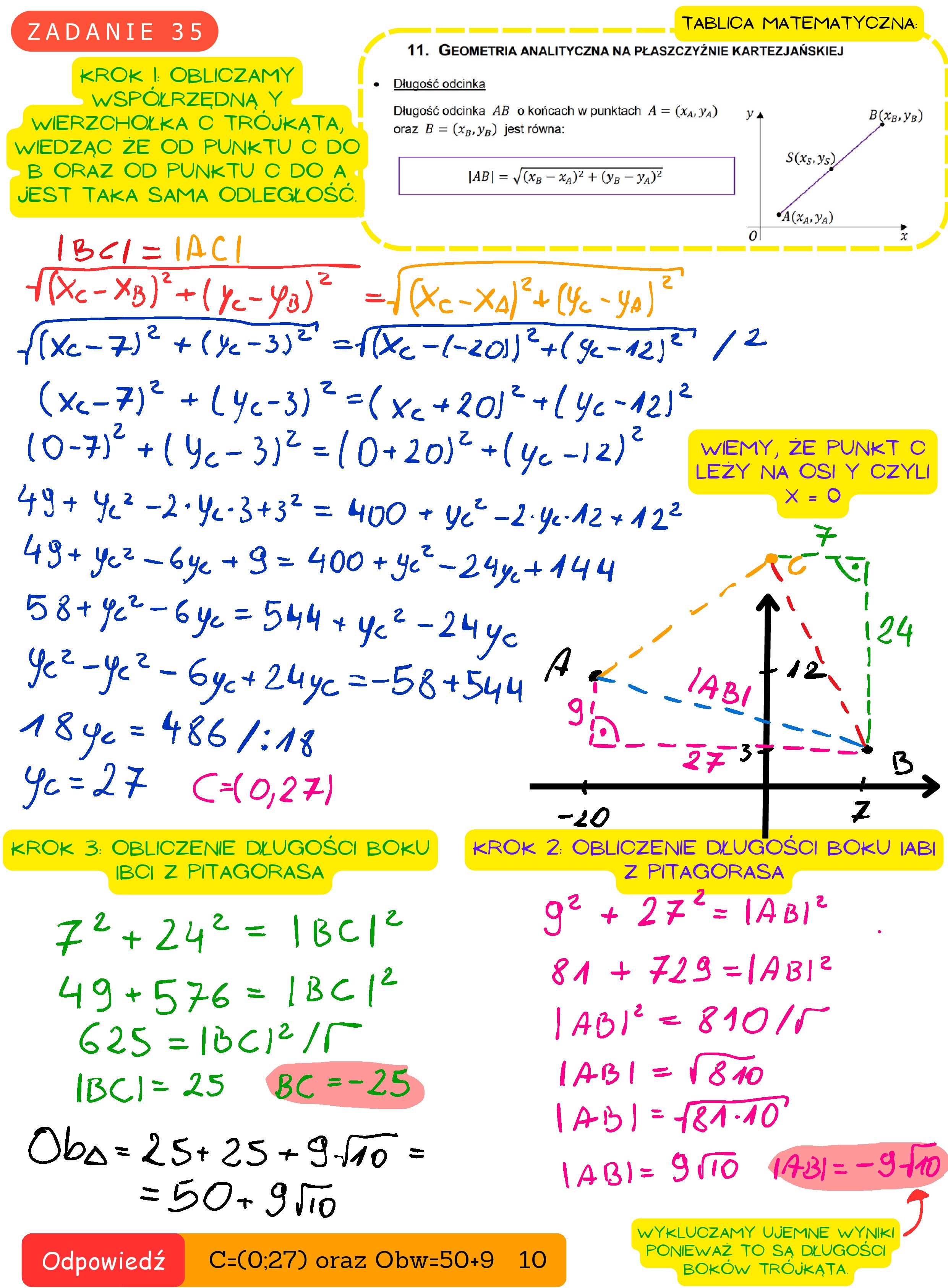
Zadanie 35. (0—5) Punkty A =(—20,12) i B=(7,3) są wierzchołkami trójkąta równoramiennego ABC, w którym |AC| = |BC|. Wierzchołek C leży naosi Oy układu współrzędnych. Oblicz współrzędne wierzchołka € oraz obwód tego trójkąta.
MATEMATYKA 2021 MAJ MATURA PODSTAWOWA

Zadanie 1. (0-1) Liczba 1007 - (0,1)"* jest równa A. 103 B. 1016 c. 1071 D. 1030

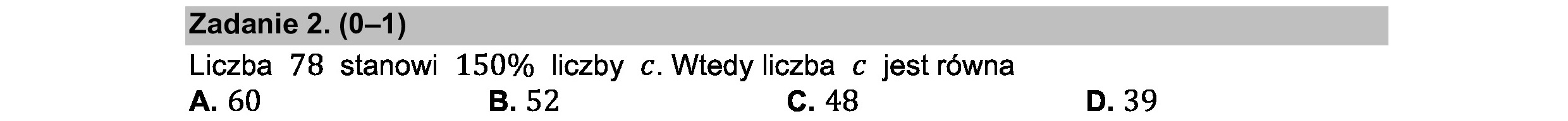
Zadanie 2. (0—1) Liczba 78 stanowi 150% liczby c. Wtedy liczba c jest równa A. 60 B. 52 C. 48 D. 39


Zadanie 3. (0-1) Rozważamy przedziały liczbowe (—0,5) i (—1 +00). Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu rozważanych przedziałów? A. 6 B. 5 Cc. 4 D. 7


Zadanie 4. (0-1) Suma 2logv10 + log 10? jest równa A. 2 B. 3 D. 5


Zadanie 5. (0—1) Różnica 0,(3) — A. —0,(39) 23 33 jest równa B.- 39 100 Cc. —0,36

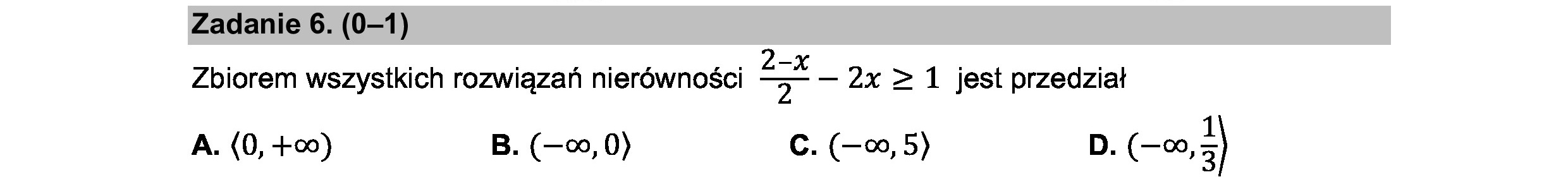
Zadanie 6. (0—1) Zbiorem wszystkich rozwiązań nierówności R — 2x2 1 jest przedział A. (0, +00) B. (—0, 0) C. (—0,5) D. (—a, 3)


Zadanie 7. (0—1) Na poniższym rysunku przedstawiono wykres funkcji f określonej w zbiorze (—6,5). Funkcja g jest określona wzorem gf(x) =f(x)—2 dla x € (—6,5). Wskaż zdanie prawdziwe. A. Liczba f(2) + g(2) jestrówna (—2). B. Zbiory wartości funkcji f i g są równe. C. Funkcje f i g mają te same miejsca zerowe. D. Punkt P = (0, —2) należy do wykresów funkcji f i g.


Zadanie 8. (0—1) Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań. Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku. y=x+1 y=x-1 A y= 2x4 c. - —2x +4 y=x-1 y=x+1 B= 2x4 D. = 244

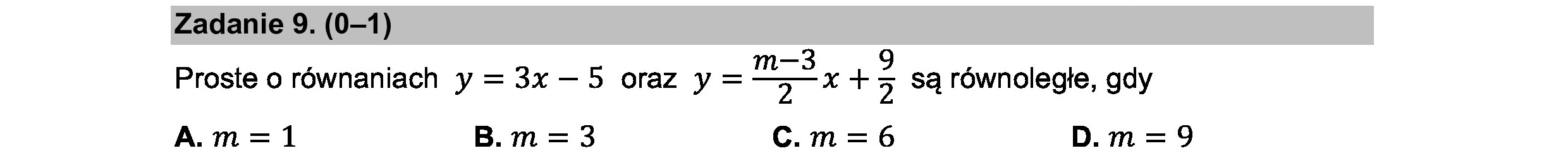
Zadanie 9. (0—1) Proste o równaniach y = 3x —5 oraz y= a. ż x +z E są równoległe, gdy A.m=1 B.m=3 c m=6 D.m=9


Zadanie 10. (0—1) Funkcja f jest określona wzorem f(x) = 3 dla każdej liczby rzeczywistej x < 1. Wtedy dla argumentu x = V3 — 1 wartość mie p jest równa A. Z B. —1 c.1 D. —_ /3—1 /3—2


Zadanie 11. (0—1) Do wykresu funkcji f określonej dla każdej liczby rzeczywistej x wzorem f(x) =3*-2 należy punkt o współrzędnych A. (—1, —5) B. (0, —2) c. (0, —1) D. (2,4)


Zadanie 12. (0—1) Funkcja kwadratowa f _ określona wzorem f(x) = —2(x + 1)(x —3) jest malejąca w przedziale A. (1, +00) B. (—o, 1) C. (—0, —8) D. (—8, +00)

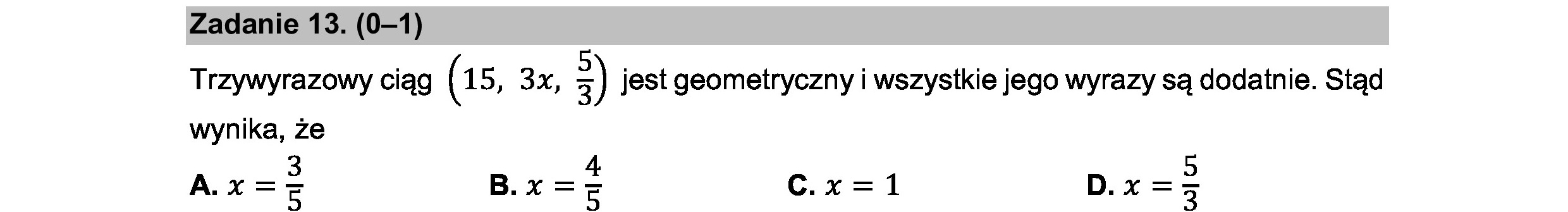
Zadanie 13. (0—1) Trzywyrazowy ciąg (15, 3x, Ą jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że 3 4 5 A.x=5 B.x=c Cc.x=1 D.x=3


Zadanie 14. (0—1) Ciąg (b„) jest określony wzorem b, = 3n? — 25n dla każdej liczby naturalnej n > 1. Liczba niedodatnich wyrazów ciągu (b„) jest równa A. 14 B. 13 Cc. 9 D. 8


Zadanie 15. (0—1) Ciąg arytmetyczny (a) jest określony dla każdej liczby naturalnej n > 1. Trzeci i piąty wyraz ciągu spełniają warunek a; + a; = 58. Wtedy czwarty wyraz tego ciągu jest równy A. 28 B. 29 Cc. 33 D. 40

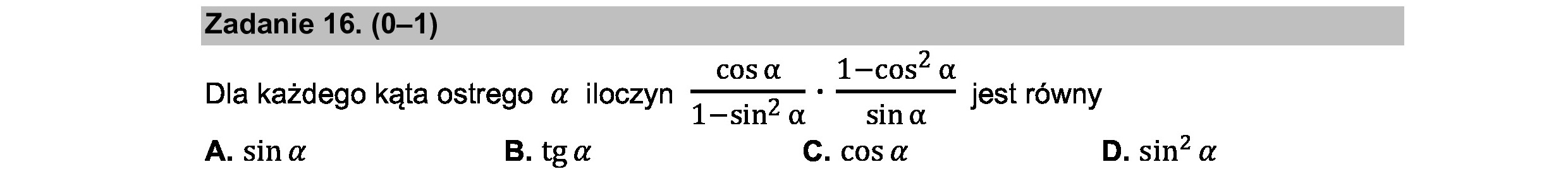
Zadanie 16. (0—1) , cos a 1-cos? a , Dla każdego kąta ostrego a iloczyn N———— * ———-- jest równy 1-sin* a sin a A. sina B. tga C. cosa D. sin? a


Zadanie 17. (0-1) Prosta k jest styczna w punkcie A do okręgu o środku O. Punkt B leży na tym okręgu i miara kąta AOB jest równa 80”. Przez punkty O i B poprowadzono prostą, która przecina prostą k w punkcie C (zobacz rysunek). Miara kąta BAC jest równa A A. 10? B. 30? c. 407 D. 50?


Zadanie 18. (0—1) Przyprostokątna AC trójkąta prostokątnego ABC ma długość 8 oraz tga =g (zobacz rysunek). Pole tego trójkąta jest równe B A. 12 B. kc 62 64 Bi c. Ka D. 5 C 8 A


Zadanie 19. (0-1) Pole pewnego trójkąta równobocznego jest równe SE) Obwód tego trójkąta jest równy 4 2 A. 4 B. 2 C.z D. z


Zadanie 20. (0—1) W trójkącie ABC bok BC madługość 13, a wysokość CD tego trójkąta dzieli bok AB na odcinki o długościach |AD| = 3 i |BD| = 12 (zobacz rysunek obok). Długość boku AC jest równa A. Vv34 B. > C. 2v14 3 13 12 D. 3V45


Zadanie 21. (0—1) Punkty A,B,C i D leżą na okręgu o środku S. Miary kątów SBC, BCD, CDA są równe odpowiednio: |4SBC| = 60”, |4BCD| = 110%, |4CDA| = 90? (zobacz rysunek). C Wynika stąd, że miara a kąta DAS jest równa >» B A. 259 B. 307 D c) c. 35? D. 40? Ś


Zadanie 22. (0—1) W równoległoboku ABCD, przedstawionym na rysunku, kąt a ma miarę 709. Wtedy kąt 8 ma miarę A. 80? B. 70? c. 60? D. 507


Zadanie 23. (0-1) W każdym n-kącie wypukłym (n > 3) liczba przekątnych jest równa 203) . Wielokątem wypukłym, w którym liczba przekątnych jesto 25 większa od liczby boków, jest A. siedmiokąt. B. dziesięciokąt. C. dwunastokąt. D. piętnastokąt.


Zadanie 24. (0—1) Pole figury Fi złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury F, złożonej z dwóch stycznych zewnętrznie kół o promieniach długości r (zobacz rysunek). Figura Fi Figura F> Długość r promienia jest równa A. 43 B. 2 c. V5 D. 3


Zadanie 25. (0-1) Punkt A = (3, —5) jest wierzchołkiem kwadratu ABCD, a punkt M = (1,3) jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu ABCD jest równe A. 68 B. 136 c. 2V34 D. 8V34


Zadanie 26. (0—1) Z wierzchołków sześcianu ABCDEFGH losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu ABCDEFGH, jest równe 1 4 1 A. 7 B. 7 C. 74 U IW


Zadanie 27. (0—1) Wszystkich liczb naturalnych trzycyfrowych, większych od 700, w których każda cyfra należy do zbioru f1,2,3,7,8,9) i żadna cyfra się nie powtarza, jest A. 108 B. 60 Cc. 40 D. 299

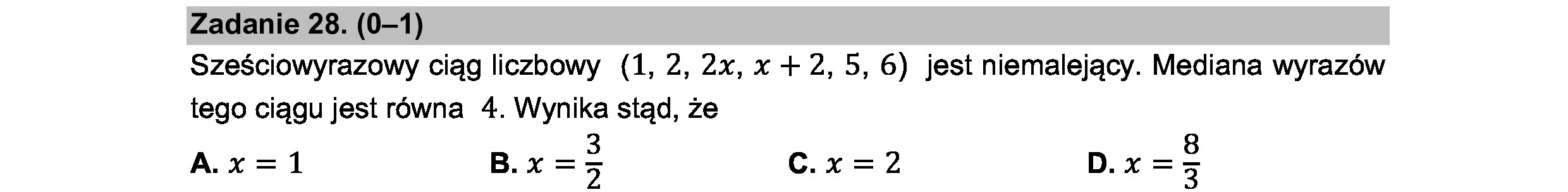
Zadanie 28. (0—1) Sześciowyrazowy ciąg liczbowy (1, 2, 2x, x + 2, 5, 6) jest niemalejący. Mediana wyrazów tego ciągu jest równa 4. Wynika stąd, że 3 8 A.x=1 B.x => C.x=2 D.x=3

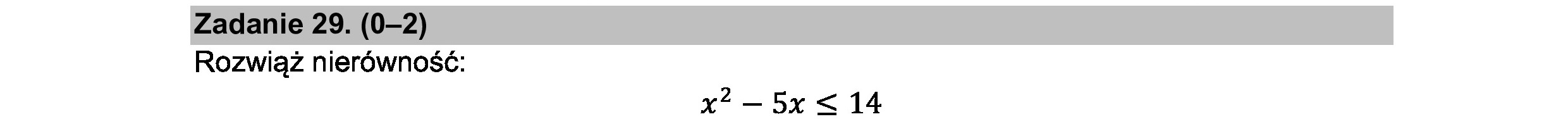
Zadanie 29. (0—2) Rozwiąż nierówność: x? —5x<14

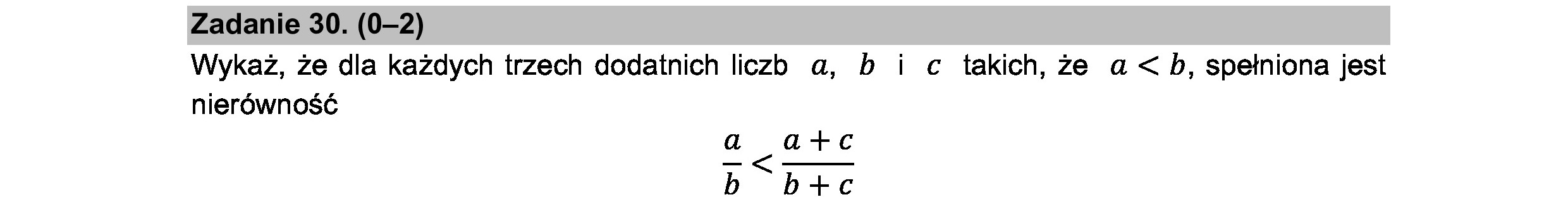
Zadanie 30. (0—2) Wykaż, że dla każdych trzech dodatnich liczb a, b i c takich, że a <b, spełniona jest nierówność a a+c b b+c


Zadanie 31. (0—2) Funkcja liniowa f przyjmuje wartość 2 dla argumentu 0, a ponadto f(4) — f(2) =6. Wyznacz wzór funkcji f.

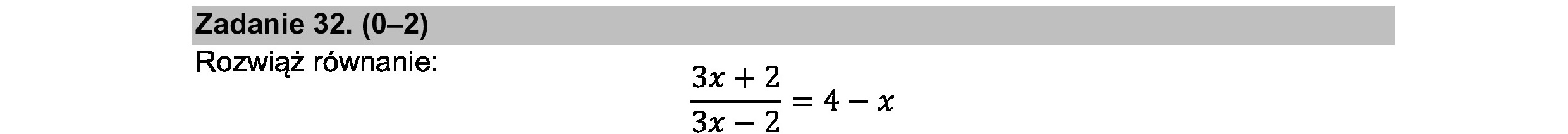
Zadanie 32. (0—2) Rozwiąż równanie: 3x +2 _ 3x—2


Zadanie 33. (0—2) Trójkąt równoboczny ABC ma pole równe 9V3. Prosta równoległa do boku BC przecina boki AB i AC — odpowiednio — w punktach K i L. Trójkąty ABC i AKL są podobne, a stosunek długości boków tych trójkątów jest równy E . Oblicz długość boku trójkąta AKL.


Zadanie 34. (0—2) Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza sumę liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że suma liczb wyrzuconych oczek jest równa 4 lub 5, lub 6.


Zadanie 35. (0—5) Punkty A =(—20,12) i B=(7,3) są wierzchołkami trójkąta równoramiennego ABC, w którym |AC| = |BC|. Wierzchołek C leży naosi Oy układu współrzędnych. Oblicz współrzędne wierzchołka € oraz obwód tego trójkąta.






























