MATEMATYKA 2021 CZERWIEC MATURA PODSTAWOWA
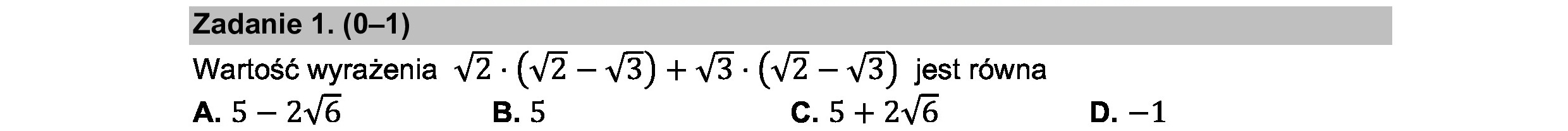
Zadanie 1. (0-1) Wartość wyrażenia V2 - (V2 — V3) + V3 : (V2 — V3) jest równa A.5—2V6 B.5 C.5+2V6 D. —1


Zadanie 2. (0—1) 2 5 13 ; 4 „A . > Liczba (7 "7 jest równa WI LT NIW A. 7 B. 71 C. 7


Zadanie 3. (0—1) Niech log; 18 = c. Wtedy log; 54 jest równy A.c1 B. c C.c+1l D.c+2


Zadanie 4. (0—1) Cenę drukarki obniżono o 20%, a następnie nową cenę obniżono o 10%. W wyniku obu tych zmian cena drukarki zmniejszyła się w stosunku do ceny sprzed obu obniżek o A 18% BR 238% Cc 30% D. 72%


Zadanie 5. (0—1) Dla każdej liczby rzeczywistej x wyrażenie (x — 1)? — (2 — x)? jest równe A.2x—-3 B. 2x? —6x —3 c. (2x — 3) D. 9


Zadanie 6. (0—1) Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich liczb rzeczywistych x, spełniających jednocześnie nierówności 0 < 7 — 3x oraz 7 —3x £<5x—3. A Z =, 5 7 4 3 x B. 7 5 7 4 3 * WNKEEEENNNENNNNNNNNE CASE 7 3 x 2 ————, HA] G1 =


Zadanie 7. (0—1) Rozwiązaniem równania xV3 + 2 = 2x — 8 jest liczba 1 V3+10 A. 10(2 + v3) B. 2 c. 10(V3 — 2) D.—


Zadanie 8. (0—1) 2— Równanie z = (0 maw zbiorze liczb rzeczywistych dokładnie A. jedno rozwiązanie. B. dwa rozwiązania. C. trzy rozwiązania. D. cztery rozwiązania.

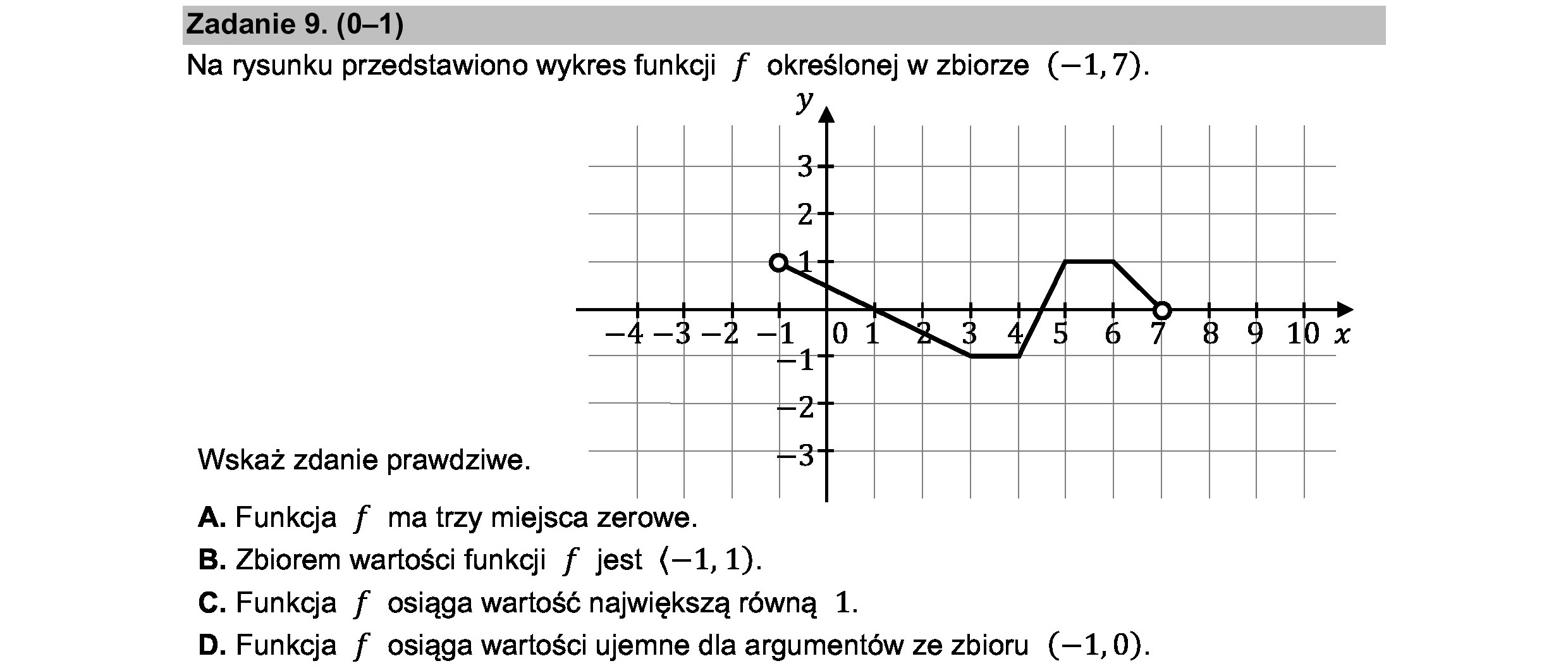
Zadanie 9. (0-1) Na rysunku przedstawiono wykres funkcji f określonej w zbiorze (—1,7). J Wskaż zdanie prawdziwe. A. Funkcja f ma trzy miejsca zerowe. B. Zbiorem wartości funkcji f jest (—1, 1). C. Funkcja f osiąga wartość największą równą 1. D. Funkcja f osiąga wartości ujemne dla argumentów ze zbioru (—1,0).


Zadanie 10. (0—1) Wykresem funkcji kwadratowej f _ określonej wzorem f(x) = —3(x + 4)(x — 2) jest parabola o wierzchołku W = (p,q). Współrzędne wierzchołka W spełniają warunki A.p>0iq>0 BBp<0iq>0 ccp<0iq<0 D.p>0iq<0

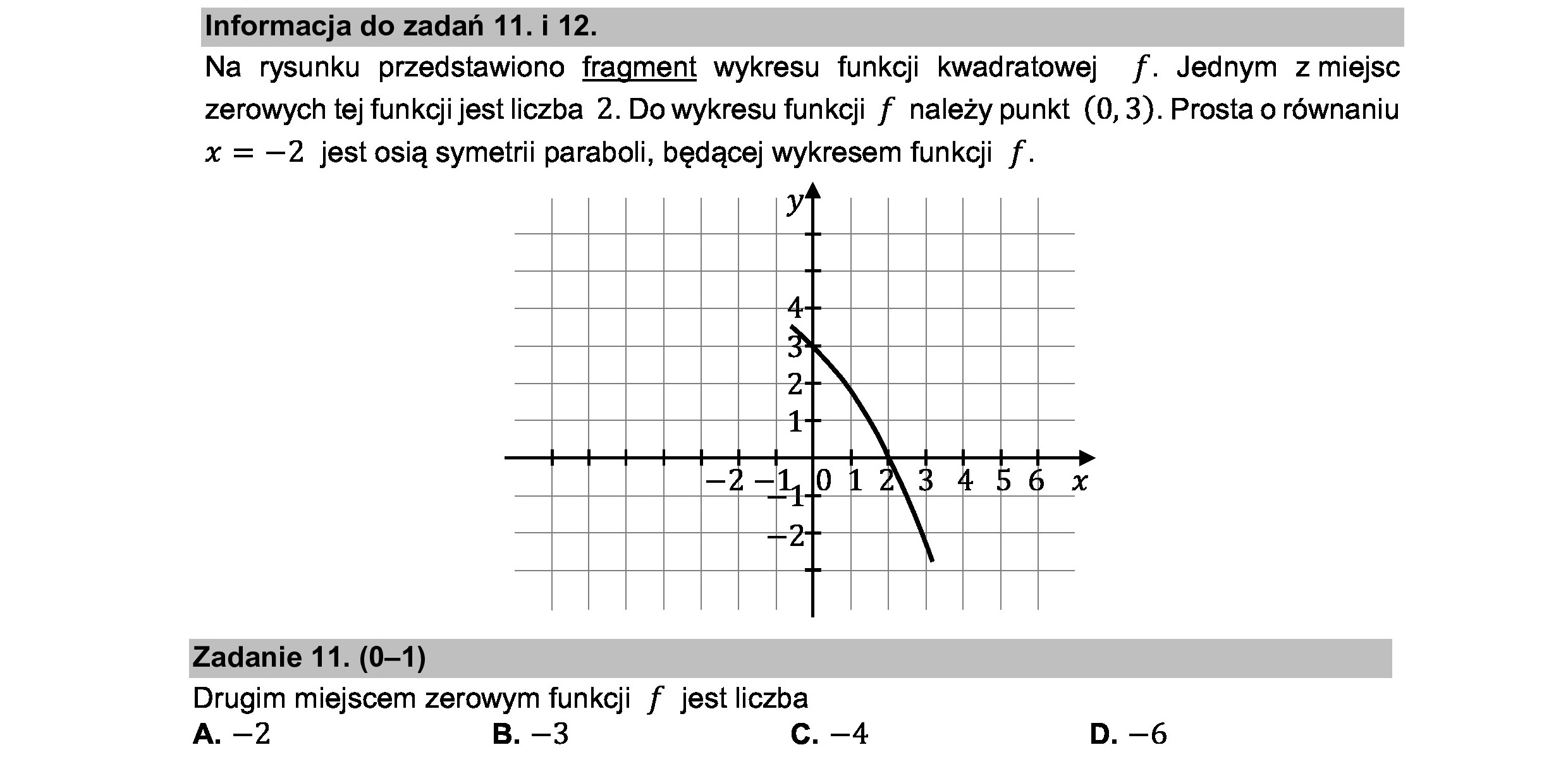
Informacja do zadań 11. i 12. Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji f należy punkt (0, 3). Prosta o równaniu x = —2 jest osią symetrii paraboli, będącej wykresem funkcji f. ; Zadanie 11. (0-1) Drugim miejscem zerowym funkcji f jest liczba A. —2 B. —3 C. —4 D. —6

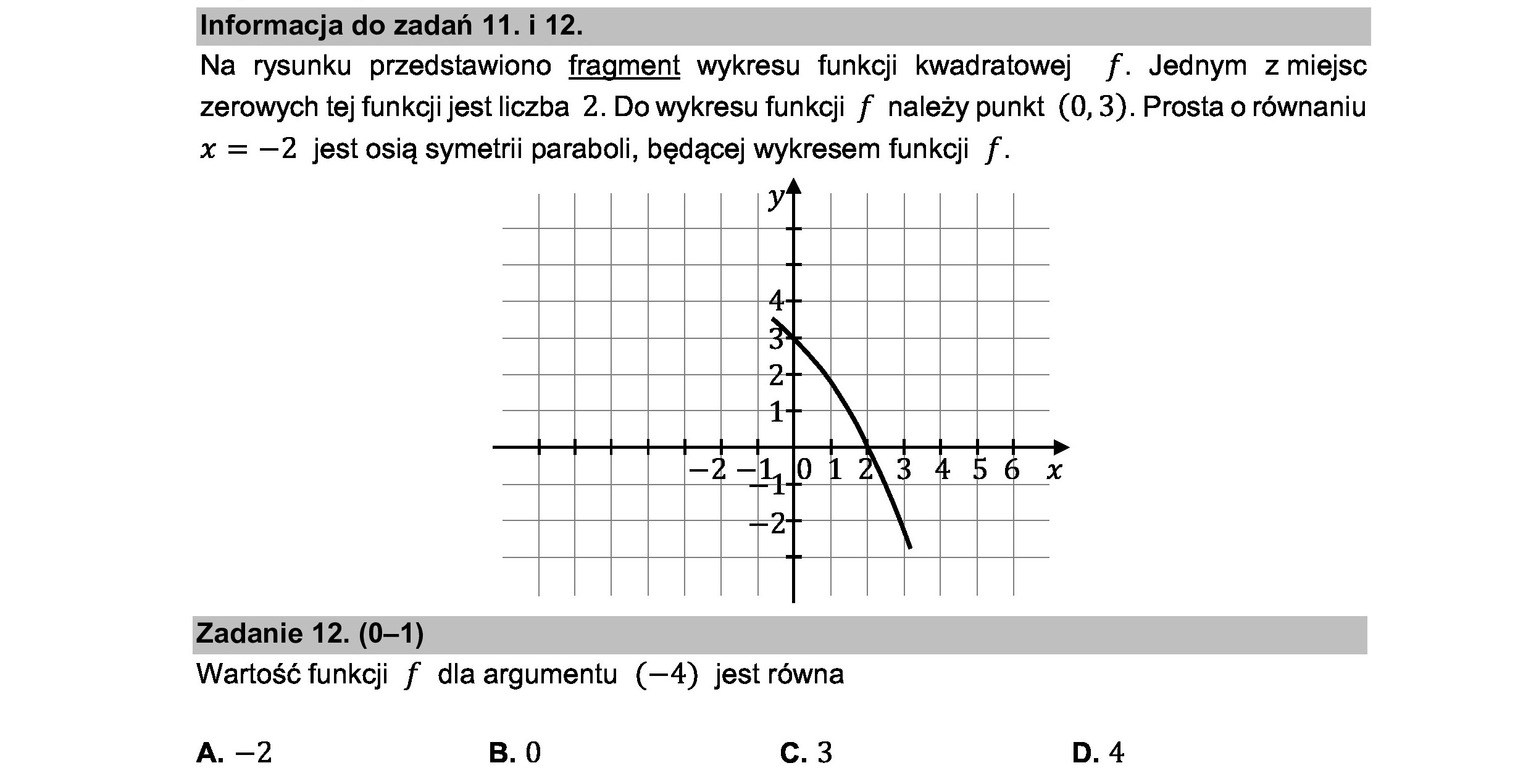
Informacja do zadań 11. i 12. Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji f należy punkt (0, 3). Prosta o równaniu x = —2 jest osią symetrii paraboli, będącej wykresem funkcji f. ; Zadanie 12. (0—1) Wartość funkcji f dla argumentu (—4) jest równa A. -2 B.0 Cc. 3 D. 4


Zadanie 13. (0—1) Dane są ciągi (an), (bn). (Cn). (dn), określone dla każdej liczby naturalnej n > 1 wzorami: a, =20n+3, b=2n2—3, cy =n+10n—2, dy ="+2"" . Liczba 197 jest dziesiątym wyrazem ciągu A. (a,) B. (b) c. (c,) D. (d,)


Zadanie 14. (0—1) Ciąg geometryczny (a,„), określony dla każdej liczby naturalnej n > 1, jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek az = a * a> . Niech q oznacza iloraz ciągu (a,„). Wtedy A.aj=3 B.a,=q C. 4 =q? D. a, = q*


Zadanie 15. (0—1) Kąt o mierze a jestostryi tga = 45. Wtedy 1 1 Ż s — [7 Zy—— A. cos a=g B. cos a= C. cos? a = aa D. cos? a = Gl u1


Zadanie 16. (0—1) Na okręgu o środku w punkcie O leżą punkty A,B oraz C. Odcinek AC jest średnicą tego okręgu, a kąt środkowy AOB ma miarę 82? (zobacz rysunek). Miara kąta OBC jest równa A. 41? B. 457 C. 49? D. 517

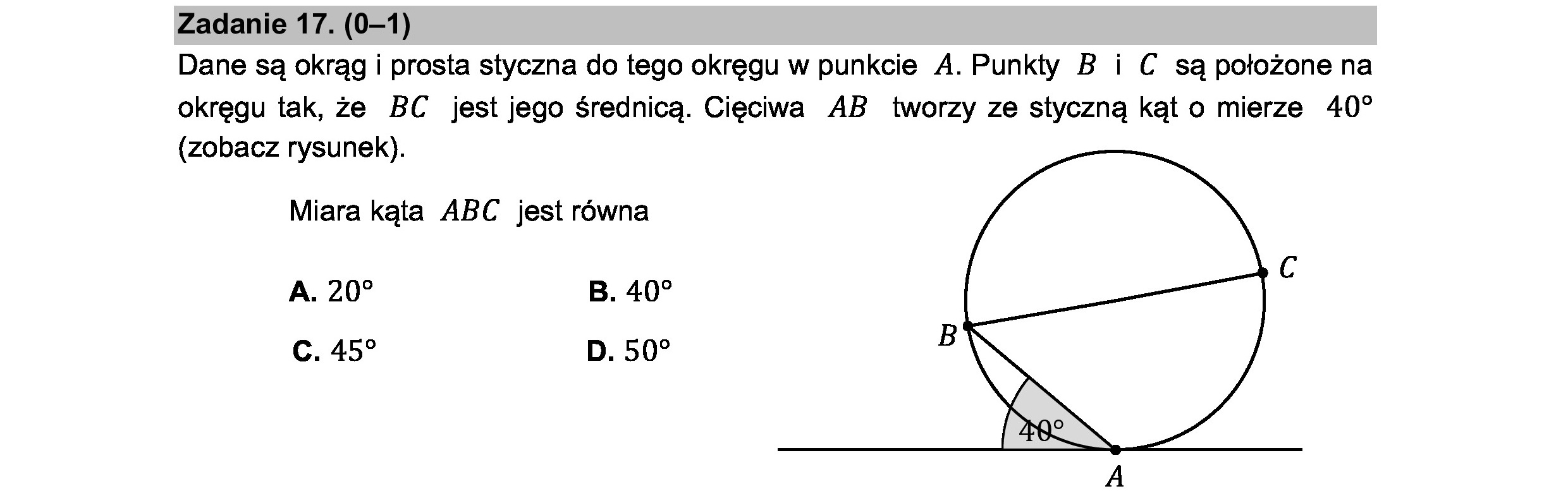
Zadanie 17. (0—1) Dane są okrąg i prosta styczna do tego okręgu w punkcie A. Punkty B i C są położone na okręgu tak, że BC jest jego średnicą. Cięciwa AB tworzy ze styczną kąt o mierze 40? (zobacz rysunek). Miara kąta ABC jest równa A. 20? B. 40? C. 450 D. 50? B U

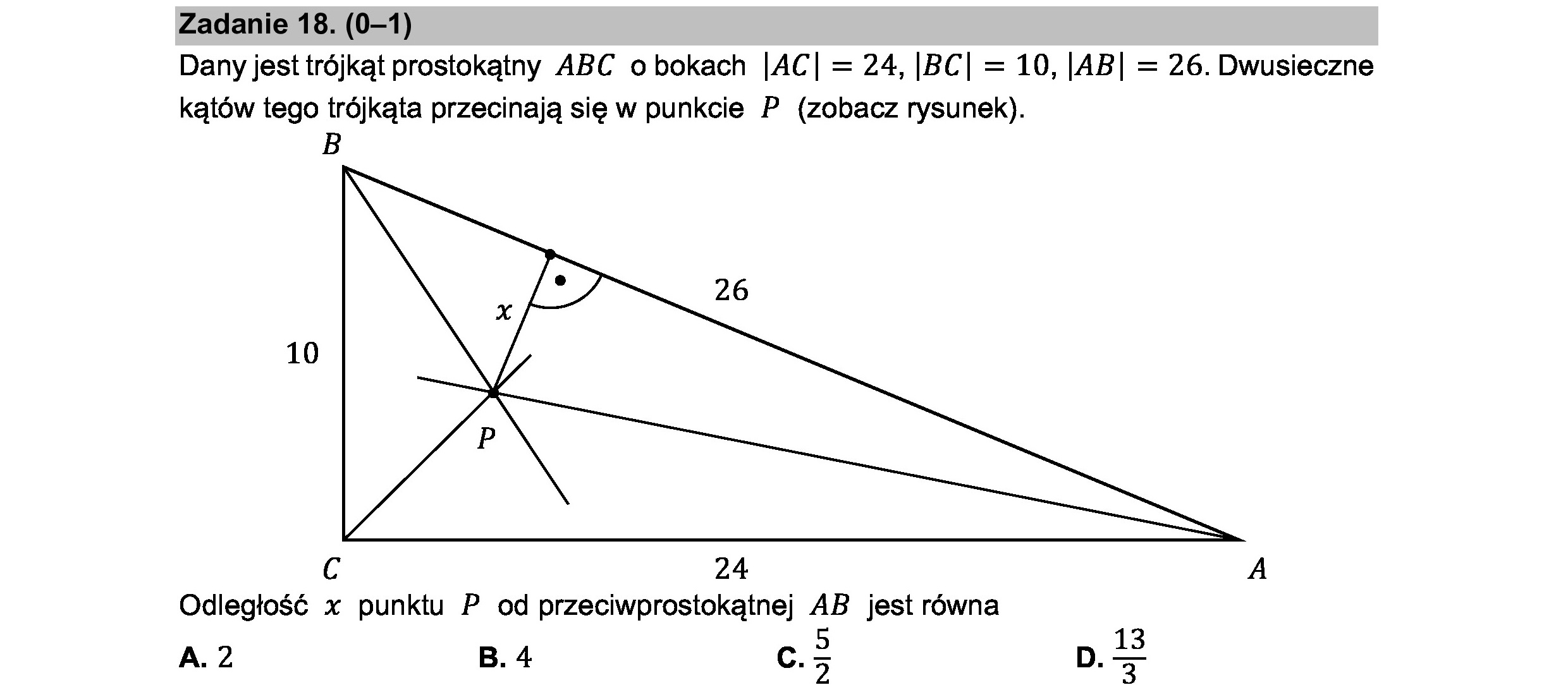
Zadanie 18. (0—1) Dany jest trójkąt prostokątny ABC o bokach |AC| = 24, |BC| = 10, |AB| = 26. Dwusieczne kątów tego trójkąta przecinają się w punkcie P (zobacz rysunek). > 26 10 G 24 A Odległość x punktu P od przeciwprostokątnej AB jest równa 5 A. 2 B. 4 C.> D.


Zadanie 19. (0—1) Jeden z boków równoległoboku ma długość równą 5. Przekątne tego równoległoboku mogą mieć długości A.4i6 B.4i3 C.10i 10 D.5i5


Zadanie 20. (0—1) W pewnym trójkącie równoramiennym największy kąt ma miarę 120”, a najdłuższy bok ma długość 12 (zobacz rysunek). Najkrótsza wysokość tego trójkąta ma długość równą <> A. 6 B. 2V3 C. 4/3 D. 6V3 12

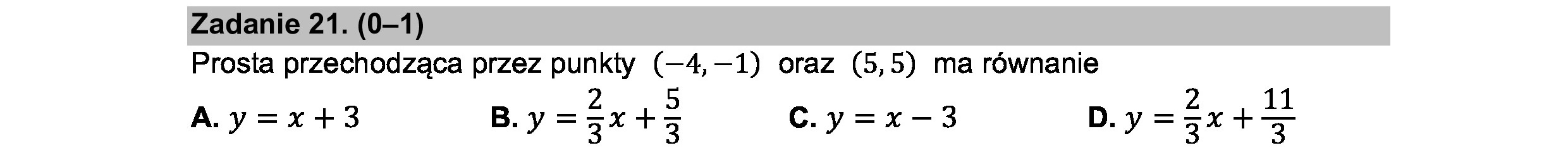
Zadanie 21. (0—1) Prosta przechodząca przez punkty (—4,—1) oraz (5,5) ma równanie A.y=x+3 B.y = gu+g CCy=x-3 DLy=zx+ 7

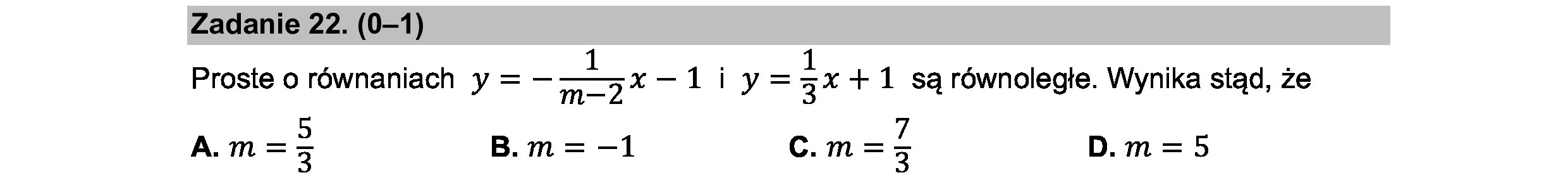
Zadanie 22. (0—1) Proste o równaniach y = — 2% —liy= zz + 1 są równoległe. Wynika stąd, że A.m=3 B.m = —1 .m=7 D.m=5


Zadanie 23. (0—1) W prostokącie ABCD dane są wierzchołki C =(—3,1) oraz D = (2,1). Bok AD ma długość 6. Pole tego prostokąta jest równe A. 6/29 B. 12V2 C. 24 D. 30


Zadanie 24. (0—1) Obrazem prostej o równaniu x — 2y + 3 = 0 wsymetrii osiowej względem osi Oy jest prosta o równaniu .->x+2y+3=0 .->x+2y-3=0 „.x+2y-3=0 „.x+2y+3=0 UOUW P


Zadanie 25. (0-1) Graniastosłup prawidłowy ma 36 krawędzi. Długość każdej z tych krawędzi jest równa 4. Pole powierzchni bocznej tego graniastosłupa jest równe A. 176 B. 192 Cc. 224 D. 288


Zadanie 26. (0—1) Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy 1 4/3 V3 A. z B. EW c.1 D. ya


Zadanie 27. (0—1) W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera — spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 25% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe A. 0,75 B. 0,25 c. ol 2 O| UL D.


Zadanie 28. (0—1) Średnia arytmetyczna czterech liczb dodatnich: 2, 3x, 3x + 2, 3x + 4 jestrówna = . Wynika stąd, że 5 A.x=9 B. x = „- C.x=g D.x=2

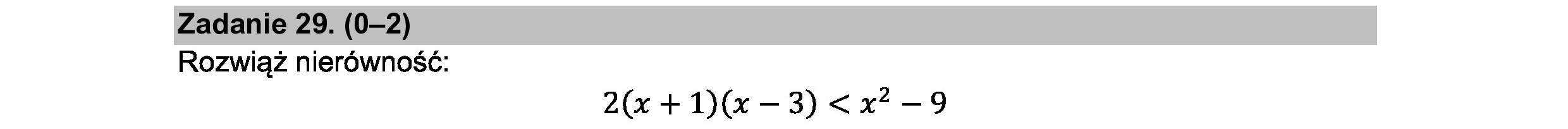
Zadanie 29. (0—2) Rozwiąż nierówność: 2(x + 1)(x —3) < x? —9

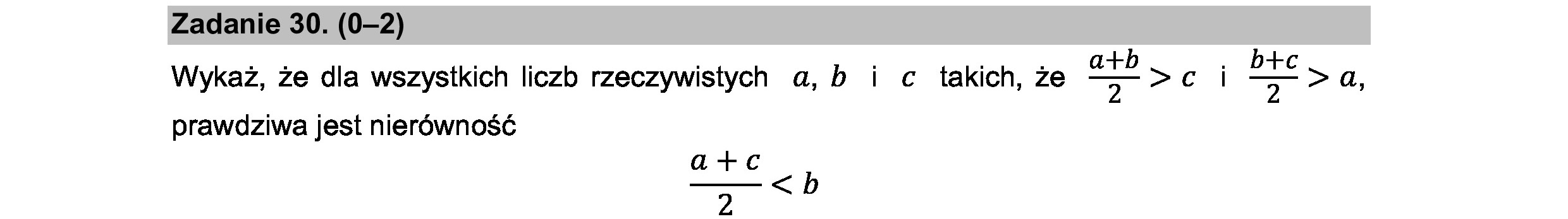
Zadanie 30. (0—2)
NE . : , , . „_ a+b „, b+c
Wykaż, że dla wszystkich liczb rzeczywistych a, b i c takich, że Tm >Cl WE >a,
prawdziwa jest nierówność
a+c
2


Zadanie 31. (0—2) Dany jest ciąg arytmetyczny (an), określony dla wszystkich liczb naturalnych n > 1. Suma dwudziestu początkowych wyrazów tego ciągu jest równa 20a, +62. Oblicz różnicę ciągu (an).


Zadanie 32. (0—2) Dany jest trapez o podstawach długości a oraz b i wysokości h. Każdą z podstaw tego trapezu wydłużono o 25%, a wysokość skrócono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent skrócono wysokość h trapezu.


Zadanie 33. (0—2) W trójkącie ABC boki BC i AC są równej długości. Prosta k jest prostopadła do podstawy AB tego trójkąta i przecina boki AB oraz BC w punktach — odpowiednio — D i E. Pole czworokąta ICE] ADEC jest 17 razy większe od pola trójkąta BED. Oblicz [EB|*


Zadanie 34. (0—2) Że zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru f£3, 4, 5, 6, 7,8), a cyfra jedności należy do zbioru f0, 1, 2,3, 4), losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.


Zadanie 35. (0—5) Podstawa AB trójkąta równoramiennego ABC jest zawarta w prostej o równaniu y = —2x + 16. Wierzchołki B i C mają współrzędne B =(3,10) i C=(—-2,3). Oblicz współrzędne wierzchołka A i pole trójkąta ABC.

MATEMATYKA 2021 CZERWIEC MATURA PODSTAWOWA
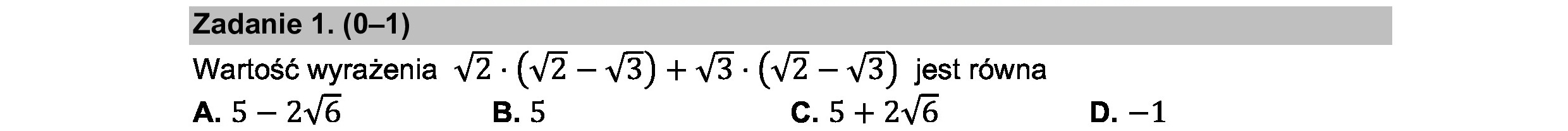
Zadanie 1. (0-1) Wartość wyrażenia V2 - (V2 — V3) + V3 : (V2 — V3) jest równa A.5—2V6 B.5 C.5+2V6 D. —1


Zadanie 2. (0—1) 2 5 13 ; 4 „A . > Liczba (7 "7 jest równa WI LT NIW A. 7 B. 71 C. 7


Zadanie 3. (0—1) Niech log; 18 = c. Wtedy log; 54 jest równy A.c1 B. c C.c+1l D.c+2


Zadanie 4. (0—1) Cenę drukarki obniżono o 20%, a następnie nową cenę obniżono o 10%. W wyniku obu tych zmian cena drukarki zmniejszyła się w stosunku do ceny sprzed obu obniżek o A 18% BR 238% Cc 30% D. 72%


Zadanie 5. (0—1) Dla każdej liczby rzeczywistej x wyrażenie (x — 1)? — (2 — x)? jest równe A.2x—-3 B. 2x? —6x —3 c. (2x — 3) D. 9


Zadanie 6. (0—1) Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich liczb rzeczywistych x, spełniających jednocześnie nierówności 0 < 7 — 3x oraz 7 —3x £<5x—3. A Z =, 5 7 4 3 x B. 7 5 7 4 3 * WNKEEEENNNENNNNNNNNE CASE 7 3 x 2 ————, HA] G1 =


Zadanie 7. (0—1) Rozwiązaniem równania xV3 + 2 = 2x — 8 jest liczba 1 V3+10 A. 10(2 + v3) B. 2 c. 10(V3 — 2) D.—


Zadanie 8. (0—1) 2— Równanie z = (0 maw zbiorze liczb rzeczywistych dokładnie A. jedno rozwiązanie. B. dwa rozwiązania. C. trzy rozwiązania. D. cztery rozwiązania.


Zadanie 9. (0-1) Na rysunku przedstawiono wykres funkcji f określonej w zbiorze (—1,7). J Wskaż zdanie prawdziwe. A. Funkcja f ma trzy miejsca zerowe. B. Zbiorem wartości funkcji f jest (—1, 1). C. Funkcja f osiąga wartość największą równą 1. D. Funkcja f osiąga wartości ujemne dla argumentów ze zbioru (—1,0).


Zadanie 10. (0—1) Wykresem funkcji kwadratowej f _ określonej wzorem f(x) = —3(x + 4)(x — 2) jest parabola o wierzchołku W = (p,q). Współrzędne wierzchołka W spełniają warunki A.p>0iq>0 BBp<0iq>0 ccp<0iq<0 D.p>0iq<0


Informacja do zadań 11. i 12. Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji f należy punkt (0, 3). Prosta o równaniu x = —2 jest osią symetrii paraboli, będącej wykresem funkcji f. ; Zadanie 11. (0-1) Drugim miejscem zerowym funkcji f jest liczba A. —2 B. —3 C. —4 D. —6


Informacja do zadań 11. i 12. Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji f należy punkt (0, 3). Prosta o równaniu x = —2 jest osią symetrii paraboli, będącej wykresem funkcji f. ; Zadanie 12. (0—1) Wartość funkcji f dla argumentu (—4) jest równa A. -2 B.0 Cc. 3 D. 4


Zadanie 13. (0—1) Dane są ciągi (an), (bn). (Cn). (dn), określone dla każdej liczby naturalnej n > 1 wzorami: a, =20n+3, b=2n2—3, cy =n+10n—2, dy ="+2"" . Liczba 197 jest dziesiątym wyrazem ciągu A. (a,) B. (b) c. (c,) D. (d,)


Zadanie 14. (0—1) Ciąg geometryczny (a,„), określony dla każdej liczby naturalnej n > 1, jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek az = a * a> . Niech q oznacza iloraz ciągu (a,„). Wtedy A.aj=3 B.a,=q C. 4 =q? D. a, = q*


Zadanie 15. (0—1) Kąt o mierze a jestostryi tga = 45. Wtedy 1 1 Ż s — [7 Zy—— A. cos a=g B. cos a= C. cos? a = aa D. cos? a = Gl u1


Zadanie 16. (0—1) Na okręgu o środku w punkcie O leżą punkty A,B oraz C. Odcinek AC jest średnicą tego okręgu, a kąt środkowy AOB ma miarę 82? (zobacz rysunek). Miara kąta OBC jest równa A. 41? B. 457 C. 49? D. 517


Zadanie 17. (0—1) Dane są okrąg i prosta styczna do tego okręgu w punkcie A. Punkty B i C są położone na okręgu tak, że BC jest jego średnicą. Cięciwa AB tworzy ze styczną kąt o mierze 40? (zobacz rysunek). Miara kąta ABC jest równa A. 20? B. 40? C. 450 D. 50? B U


Zadanie 18. (0—1) Dany jest trójkąt prostokątny ABC o bokach |AC| = 24, |BC| = 10, |AB| = 26. Dwusieczne kątów tego trójkąta przecinają się w punkcie P (zobacz rysunek). > 26 10 G 24 A Odległość x punktu P od przeciwprostokątnej AB jest równa 5 A. 2 B. 4 C.> D.


Zadanie 19. (0—1) Jeden z boków równoległoboku ma długość równą 5. Przekątne tego równoległoboku mogą mieć długości A.4i6 B.4i3 C.10i 10 D.5i5


Zadanie 20. (0—1) W pewnym trójkącie równoramiennym największy kąt ma miarę 120”, a najdłuższy bok ma długość 12 (zobacz rysunek). Najkrótsza wysokość tego trójkąta ma długość równą <> A. 6 B. 2V3 C. 4/3 D. 6V3 12

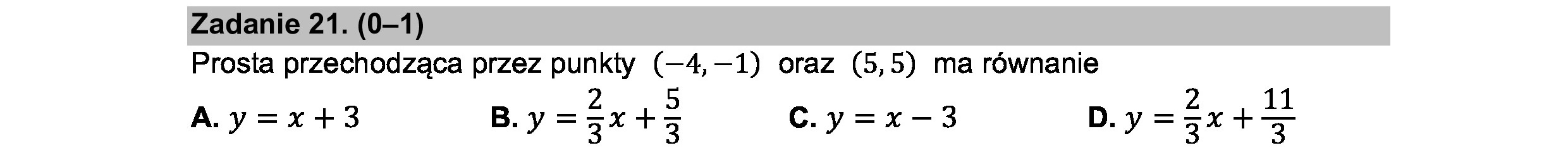
Zadanie 21. (0—1) Prosta przechodząca przez punkty (—4,—1) oraz (5,5) ma równanie A.y=x+3 B.y = gu+g CCy=x-3 DLy=zx+ 7

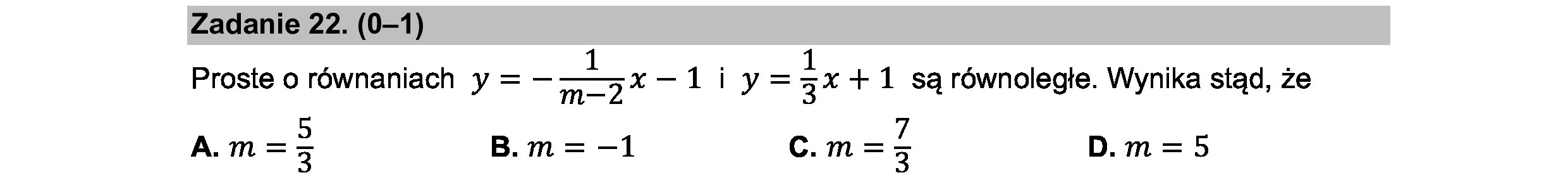
Zadanie 22. (0—1) Proste o równaniach y = — 2% —liy= zz + 1 są równoległe. Wynika stąd, że A.m=3 B.m = —1 .m=7 D.m=5


Zadanie 23. (0—1) W prostokącie ABCD dane są wierzchołki C =(—3,1) oraz D = (2,1). Bok AD ma długość 6. Pole tego prostokąta jest równe A. 6/29 B. 12V2 C. 24 D. 30


Zadanie 24. (0—1) Obrazem prostej o równaniu x — 2y + 3 = 0 wsymetrii osiowej względem osi Oy jest prosta o równaniu .->x+2y+3=0 .->x+2y-3=0 „.x+2y-3=0 „.x+2y+3=0 UOUW P


Zadanie 25. (0-1) Graniastosłup prawidłowy ma 36 krawędzi. Długość każdej z tych krawędzi jest równa 4. Pole powierzchni bocznej tego graniastosłupa jest równe A. 176 B. 192 Cc. 224 D. 288


Zadanie 26. (0—1) Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy 1 4/3 V3 A. z B. EW c.1 D. ya


Zadanie 27. (0—1) W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera — spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 25% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe A. 0,75 B. 0,25 c. ol 2 O| UL D.


Zadanie 28. (0—1) Średnia arytmetyczna czterech liczb dodatnich: 2, 3x, 3x + 2, 3x + 4 jestrówna = . Wynika stąd, że 5 A.x=9 B. x = „- C.x=g D.x=2

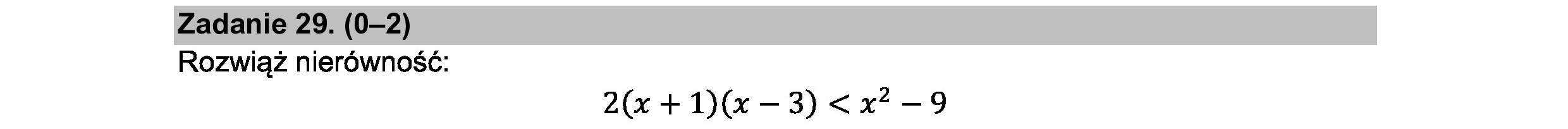
Zadanie 29. (0—2) Rozwiąż nierówność: 2(x + 1)(x —3) < x? —9

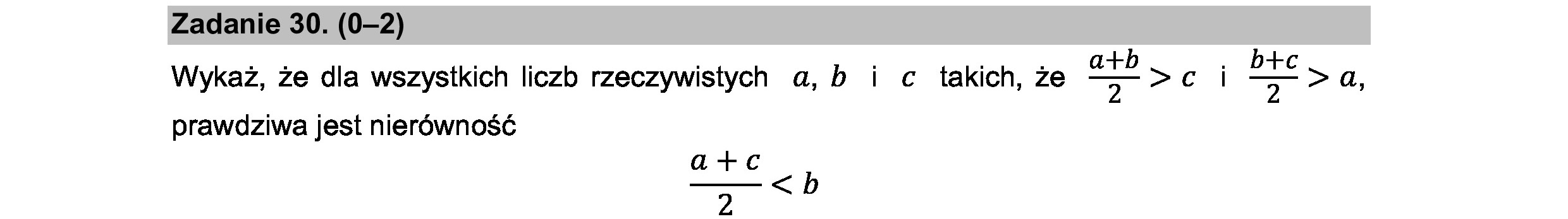
Zadanie 30. (0—2) NE . : , , . „_ a+b „, b+c Wykaż, że dla wszystkich liczb rzeczywistych a, b i c takich, że Tm >Cl WE >a, prawdziwa jest nierówność a+c 2 <b


Zadanie 31. (0—2) Dany jest ciąg arytmetyczny (an), określony dla wszystkich liczb naturalnych n > 1. Suma dwudziestu początkowych wyrazów tego ciągu jest równa 20a, +62. Oblicz różnicę ciągu (an).


Zadanie 32. (0—2) Dany jest trapez o podstawach długości a oraz b i wysokości h. Każdą z podstaw tego trapezu wydłużono o 25%, a wysokość skrócono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent skrócono wysokość h trapezu.


Zadanie 33. (0—2) W trójkącie ABC boki BC i AC są równej długości. Prosta k jest prostopadła do podstawy AB tego trójkąta i przecina boki AB oraz BC w punktach — odpowiednio — D i E. Pole czworokąta ICE] ADEC jest 17 razy większe od pola trójkąta BED. Oblicz [EB|*


Zadanie 34. (0—2) Że zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru f£3, 4, 5, 6, 7,8), a cyfra jedności należy do zbioru f0, 1, 2,3, 4), losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.


Zadanie 35. (0—5) Podstawa AB trójkąta równoramiennego ABC jest zawarta w prostej o równaniu y = —2x + 16. Wierzchołki B i C mają współrzędne B =(3,10) i C=(—-2,3). Oblicz współrzędne wierzchołka A i pole trójkąta ABC.






























