MATEMATYKA 2020 LIPIEC MATURA PODSTAWOWA
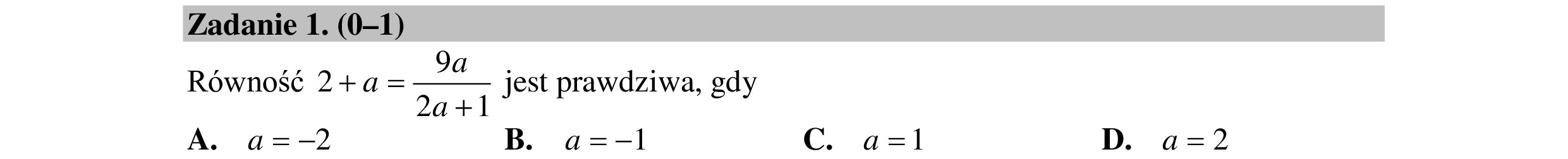
Zadanie 1. (0—1) Równość 2+a= 7 A. a=2 Ja a + i jest prawdziwa, gdy B. a=—1


Liczba 1— (27 — 1) jest równa A. -25 B 2..27 c 2-327 Do 27-29 42


Liczba log p, 4 jest równa A. 2 B. 4 c. 32 D. 16


Zadanie 4. (0—1) Masę Słońca równą 1,989-10”kg przybliżono do 2-10”kg. Błąd bezwzględny tego przybliżenia jest równy A. 0,0011-10%0kg _ B. 1,1-10% kg C. 011-107 kg D. 0,011-1090 kg


Zadanie 5. (0—1) |. . . " , | 2 : Największą liczbą całkowitą spełniającą nierówność ra s Pa 3 x+4 jest A. -3 B. — c. 2 D. 3


Zadanie 6. (0—1) |= . | : Równanie ——— = 2x w zbiorze liczb całkowitych x nie ma żadnego rozwiązania. Li ma dokładnie jedno rozwiązanie. ma dokładnie dwa rozwiązania. SOP ma więcej niż dwa rozwiązania.

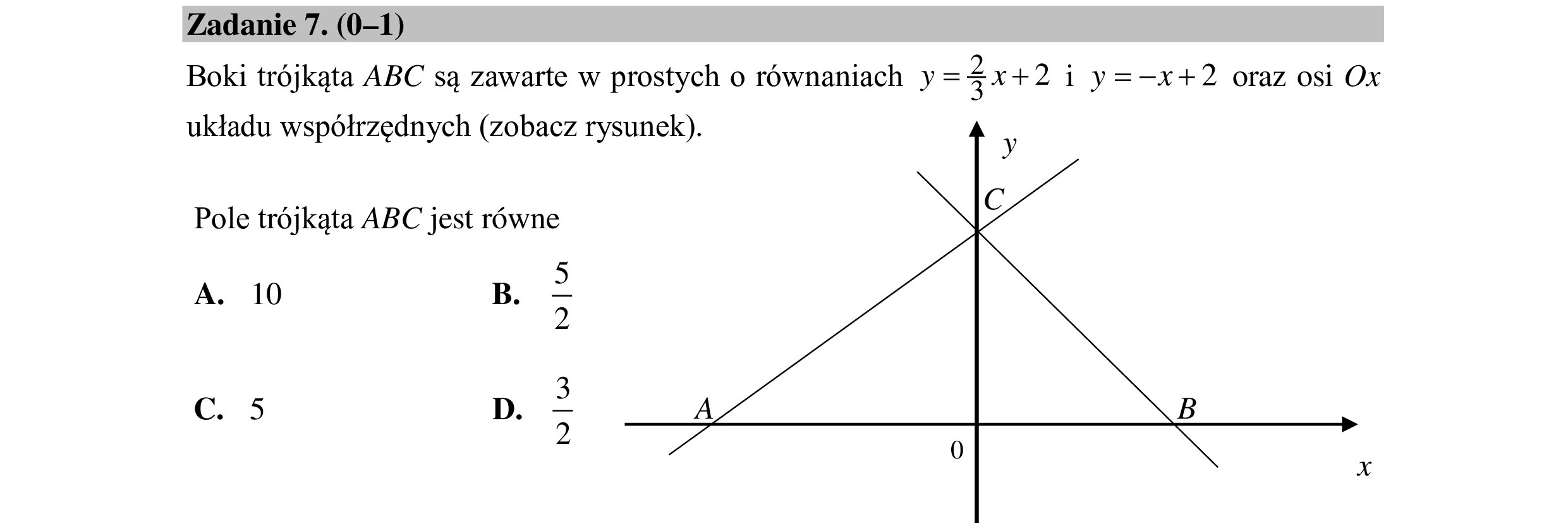
Zadanie 7. (0—1) Boki trójkąta ABC są zawarte w prostych o równaniach y= żx+ 2i y=—x+2 oraz osi Ox układu współrzędnych (zobacz rysunek). Pole trójkąta ABC jest równe A. 10 B. ś p C. 5 p. > 2


Zadanie 8. (0—1) Punkt P =(—3,7) leży na wykresie funkcji liniowej f określonej wzorem f(x) =(2m-1)x+5. Zatem | 5 A. m=— B. m=-—— Cc. m=— D. m=—— 6 6


Zadanie 9. (0—1) Wykresem funkcji kwadratowej f określonej wzorem f(x)=—w +6x+4 jest parabola o wierzchołku w punkcie (3, q). Liczba q jest równa A. 4 B. 7 c. 9 D. 13


Zadanie 10. (0—1) Funkcja f każdej liczbie naturalnej n> 1 przyporządkowuje resztę z dzielenia tej liczby przez 4. Zbiorem wartości funkcji f jest A. f0,1,2,3) B. (1,2,3,4) c. (0,1,2,3,4) D. 40,2)

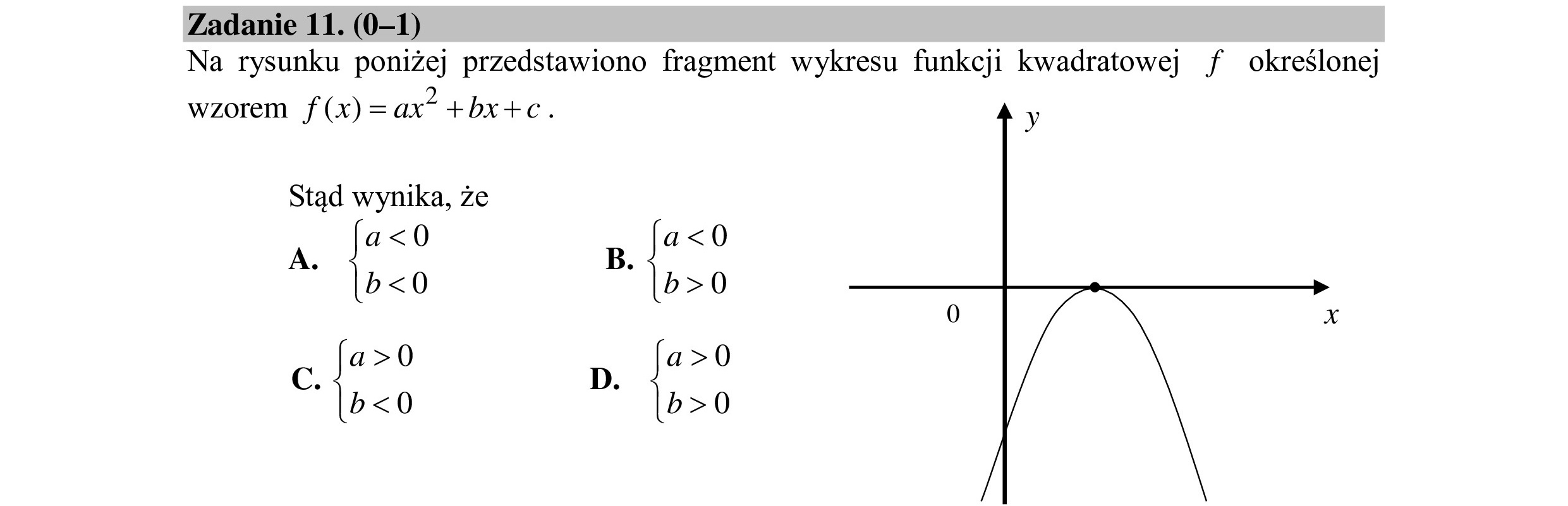
Zadanie 11. (0—1) Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej f określonej wzorem f(x)= ax” +bx+c. y Stąd wynika, że a<0 a<0 B. b<0 b>0 a>0 a>0 c. D. zo zo


Zadanie 12. (0—1) Proste o równaniach y=(m—2)x oraz y= z» +7 są prostopadłe. Wtedy A. mi=—. B. mL. c. mea i D. m 4 3 4 3


Zadanie 13. (0—1) Ciąg arytmetyczny (a, ) jest określony dla każdej liczby naturalnej n > 1. Czwarty wyraz tego ciągu jest równy a, = 2020. Suma a, +a, jest równa A. 505 B. 1010 c. 2020 D. 4040


Zadanie 14. (0—1) Ciąg geometryczny (a,) jest określony dla każdej liczby naturalnej n > 1 oraz a, =6 i a, =—48. Wynika stąd, że A. a,>0 B. a,<0 C. a,>a, D. a,>a;


Zadanie 15. (0—1) Punkty A= (80,—1) i B =(—6,—19) są wierzchołkami trójkąta prostokątnego ABC. W tym trójkącie kąt przy wierzchołku C jest prosty. Środkiem okręgu opisanego na tym trójkącie jest punkt o współrzędnych A. (43,-10) B. (37,10) c. (43,10) D. (37,—10)


Zadanie 16. (0—1) W trapezie prostokątnym ABCD są dane długości boków: [AB] =8, BC | =5, |DC | aś; AD| =4 (zobacz rysunek). D > C Tangens kąta ostrego ABC w tym trapezie jest równy 5 4 4 3 A. - B. — > Ś 4 3 5 c. 4 D. 5


Zadanie 17. (0—1) Punkty A=(1,-2) i C=(0,5) są końcami przekątnej kwadratu ABCD. Obwód tego kwadratu jest równy A. 12 B. 20 C. 28 D. 48


Zadanie 18. (0—1) Pole trójkąta równoramiennego jest równe 2542 . Miara kąta między ramionami tego trójkąta jest równa 457. Każde z ramion tego trójkąta ma długość A. 10/2 B. 54/2 Cc. 5 D. 10


Zadanie 19. (0—1)
Dany jest trójkąt prostokątny ABC, w którym przyprostokątna BC ma długość 250 cm,
a przyprostokątna AC ma długość 91 cm. Miara 5 kąta ABC spełnia warunek
A. 199

Zadanie 20. (0—1) Tworząca stożka jest o 2 dłuższa od promienia jego podstawy, a pole powierzchni bocznej jest o 2n większe od pola podstawy. Promień podstawy tego stożka jest równy A. 3 B. 21 c. I D. n


Zadanie 21. (0—1) Objętość ostrosłupa prawidłowego czworokątnego, w którym wysokość jest dwa razy dłuższa od krawędzi podstawy, jest równa 144. Długość krawędzi podstawy tego ostrosłupa jest równa A. 18 B. 36 c. 3 D. 6

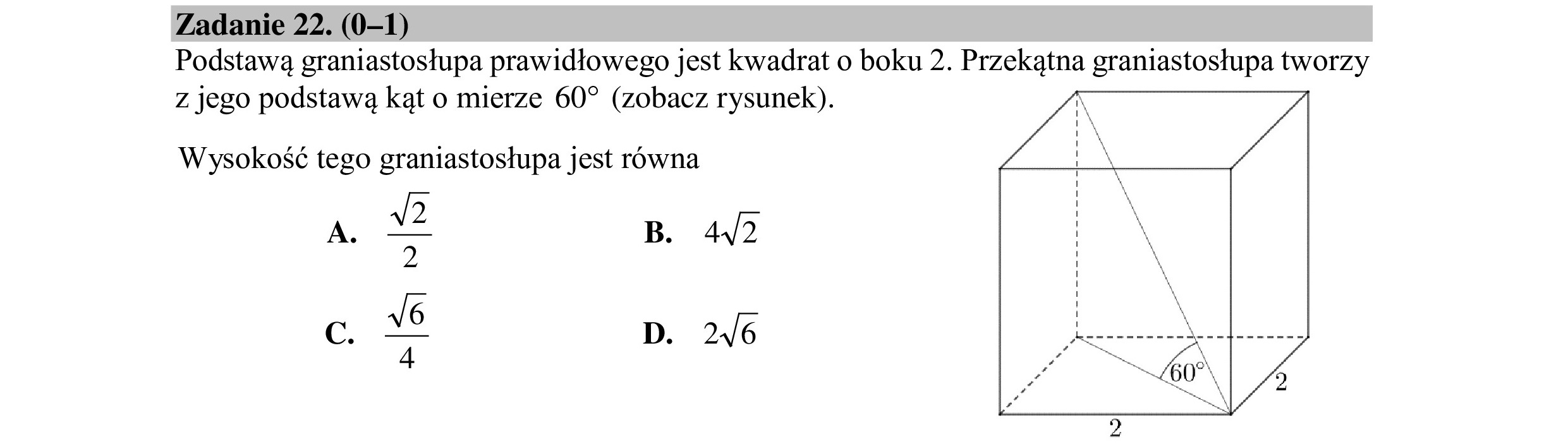
Zadanie 22. (0—1) Podstawą graniastosłupa prawidłowego jest kwadrat o boku 2. Przekątna graniastosłupa tworzy z jego podstawą kąt o mierze 60” (zobacz rysunek). Ń Wysokość tego graniastosłupa jest równa 4 B. 44/2 A A. c. | wś D. 246 prz ó 60


Zadanie 23. (0—1) Wszystkich czterocyfrowych liczb naturalnych, w których cyfra tysięcy i cyfra setek są większe od 4, a każda z pozostałych cyfr jest mniejsza od 6, jest A. 4:4.5-5 B. 5:4-:6:5 C. 5.:5.6:6 D. 4.3.5-4


Zadanie 24. (0—1) Wariancją zestawu czterech ocen z matematyki: 1, 3,5, 3, jest liczba A. I B. 2 c. 3


Zadanie 25. (0—1) W urnie jest 9 kul, w tym cztery kule czerwone, trzy zielone i dwie kule białe. Losujemy jedną kulę. Prawdopodobieństwo, że nie wylosowano ani kuli zielonej, ani białej, jest równe A. Ż B. > c. > p. * 5 9 9 9


Rozwiąż nierówność (2x+5)(3x-1)>0.

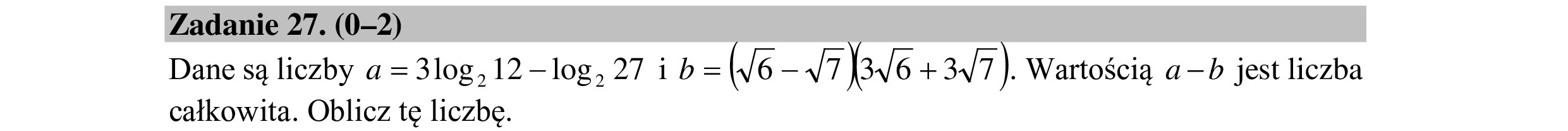
Zadanie 27. (0—2) Dane są liczby a = 3log, 12- log, 27 i b=(4/6-4T)BV6 + 34/7). Wartością a —b jest liczba całkowita. Oblicz tę liczbę.

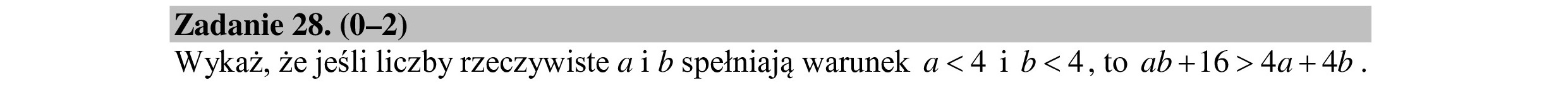
Zadanie 28. (0—2) Wykaż, że jeśli liczby rzeczywiste a i b spełniają warunek a<4 i b<4,to ab+16>4a+4b.

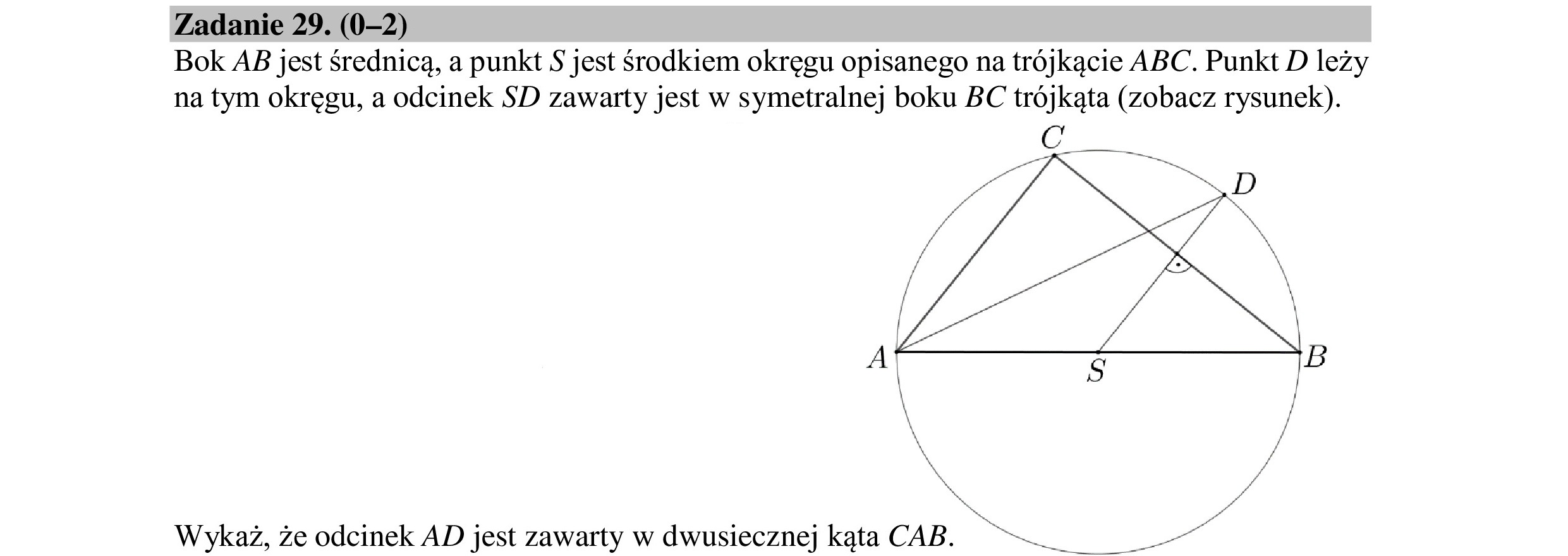
Zadanie 29. (0—2) Bok AB jest średnicą, a punkt S jest środkiem okręgu opisanego na trójkącie ABC. Punkt D leży na tym okręgu, a odcinek SD zawarty jest w symetralnej boku BC trójkąta (zobacz rysunek). Wykaż, że odcinek AD jest zawarty w dwusiecznej kąta CAB. KE

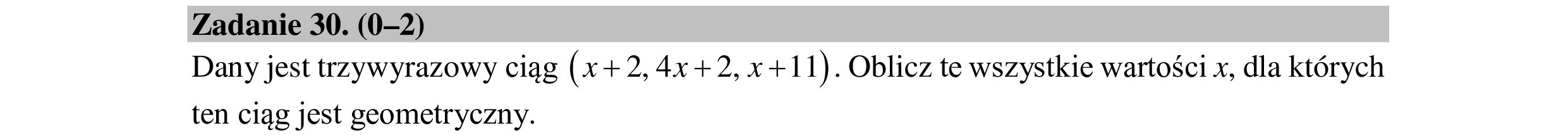
Zadanie 30. (0—2) Dany jest trzywyrazowy ciąg (x +2,4x+2,x+1 1) . Oblicz te wszystkie wartości x, dla których ten ciąg jest geometryczny.


Zadanie 31. (0—2) Prosta k jest nachylona do osi Ox pod kątem ostrym a, takim, że cosa= . Wyznacz »|śr współczynnik kierunkowy prostej k.

Zadanie 32. (0—4) Punkty A= (1-1) ,B= (6,1) „C= (7,5) i D= (2,4) są wierzchołkami czworokąta ABCD. Oblicz współrzędne punktu przecięcia przekątnych tego czworokąta.

Zadanie 33. (0—4) Rzucamy cztery razy symetryczną monetą. Oblicz prawdopodobieństwo zdarzenia A, polegającego na tym, że liczba otrzymanych orłów będzie różna od liczby otrzymanych reszek.


Zadanie 34. (0—5) W ostrosłupie prawidłowym sześciokątnym ABCDEFS, którego krawędź podstawy a ma długość 8 (zobacz rysunek), ściana boczna jest nachylona do płaszczyzny podstawy pod kątem a =60”. Oblicz cosinus kąta między krawędzią boczną a płaszczyzną podstawy tego ostrosłupa. S

MATEMATYKA 2020 LIPIEC MATURA PODSTAWOWA
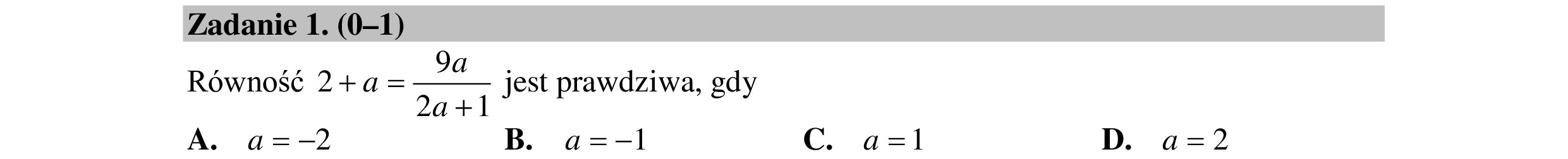
Zadanie 1. (0—1) Równość 2+a= 7 A. a=2 Ja a + i jest prawdziwa, gdy B. a=—1


Liczba 1— (27 — 1) jest równa A. -25 B 2..27 c 2-327 Do 27-29 42


Liczba log p, 4 jest równa A. 2 B. 4 c. 32 D. 16


Zadanie 4. (0—1) Masę Słońca równą 1,989-10”kg przybliżono do 2-10”kg. Błąd bezwzględny tego przybliżenia jest równy A. 0,0011-10%0kg _ B. 1,1-10% kg C. 011-107 kg D. 0,011-1090 kg


Zadanie 5. (0—1) |. . . " , | 2 : Największą liczbą całkowitą spełniającą nierówność ra s Pa 3 x+4 jest A. -3 B. — c. 2 D. 3


Zadanie 6. (0—1) |= . | : Równanie ——— = 2x w zbiorze liczb całkowitych x nie ma żadnego rozwiązania. Li ma dokładnie jedno rozwiązanie. ma dokładnie dwa rozwiązania. SOP ma więcej niż dwa rozwiązania.


Zadanie 7. (0—1) Boki trójkąta ABC są zawarte w prostych o równaniach y= żx+ 2i y=—x+2 oraz osi Ox układu współrzędnych (zobacz rysunek). Pole trójkąta ABC jest równe A. 10 B. ś p C. 5 p. > 2


Zadanie 8. (0—1) Punkt P =(—3,7) leży na wykresie funkcji liniowej f określonej wzorem f(x) =(2m-1)x+5. Zatem | 5 A. m=— B. m=-—— Cc. m=— D. m=—— 6 6


Zadanie 9. (0—1) Wykresem funkcji kwadratowej f określonej wzorem f(x)=—w +6x+4 jest parabola o wierzchołku w punkcie (3, q). Liczba q jest równa A. 4 B. 7 c. 9 D. 13


Zadanie 10. (0—1) Funkcja f każdej liczbie naturalnej n> 1 przyporządkowuje resztę z dzielenia tej liczby przez 4. Zbiorem wartości funkcji f jest A. f0,1,2,3) B. (1,2,3,4) c. (0,1,2,3,4) D. 40,2)


Zadanie 11. (0—1) Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej f określonej wzorem f(x)= ax” +bx+c. y Stąd wynika, że a<0 a<0 B. b<0 b>0 a>0 a>0 c. D. zo zo


Zadanie 12. (0—1) Proste o równaniach y=(m—2)x oraz y= z» +7 są prostopadłe. Wtedy A. mi=—. B. mL. c. mea i D. m 4 3 4 3


Zadanie 13. (0—1) Ciąg arytmetyczny (a, ) jest określony dla każdej liczby naturalnej n > 1. Czwarty wyraz tego ciągu jest równy a, = 2020. Suma a, +a, jest równa A. 505 B. 1010 c. 2020 D. 4040


Zadanie 14. (0—1) Ciąg geometryczny (a,) jest określony dla każdej liczby naturalnej n > 1 oraz a, =6 i a, =—48. Wynika stąd, że A. a,>0 B. a,<0 C. a,>a, D. a,>a;


Zadanie 15. (0—1) Punkty A= (80,—1) i B =(—6,—19) są wierzchołkami trójkąta prostokątnego ABC. W tym trójkącie kąt przy wierzchołku C jest prosty. Środkiem okręgu opisanego na tym trójkącie jest punkt o współrzędnych A. (43,-10) B. (37,10) c. (43,10) D. (37,—10)


Zadanie 16. (0—1) W trapezie prostokątnym ABCD są dane długości boków: [AB] =8, BC | =5, |DC | aś; AD| =4 (zobacz rysunek). D > C Tangens kąta ostrego ABC w tym trapezie jest równy 5 4 4 3 A. - B. — > Ś 4 3 5 c. 4 D. 5


Zadanie 17. (0—1) Punkty A=(1,-2) i C=(0,5) są końcami przekątnej kwadratu ABCD. Obwód tego kwadratu jest równy A. 12 B. 20 C. 28 D. 48


Zadanie 18. (0—1) Pole trójkąta równoramiennego jest równe 2542 . Miara kąta między ramionami tego trójkąta jest równa 457. Każde z ramion tego trójkąta ma długość A. 10/2 B. 54/2 Cc. 5 D. 10


Zadanie 19. (0—1) Dany jest trójkąt prostokątny ABC, w którym przyprostokątna BC ma długość 250 cm, a przyprostokątna AC ma długość 91 cm. Miara 5 kąta ABC spełnia warunek A. 199<B<219 B. 219< 8 < 239 C. 679< <69? D. 699< B<719


Zadanie 20. (0—1) Tworząca stożka jest o 2 dłuższa od promienia jego podstawy, a pole powierzchni bocznej jest o 2n większe od pola podstawy. Promień podstawy tego stożka jest równy A. 3 B. 21 c. I D. n


Zadanie 21. (0—1) Objętość ostrosłupa prawidłowego czworokątnego, w którym wysokość jest dwa razy dłuższa od krawędzi podstawy, jest równa 144. Długość krawędzi podstawy tego ostrosłupa jest równa A. 18 B. 36 c. 3 D. 6


Zadanie 22. (0—1) Podstawą graniastosłupa prawidłowego jest kwadrat o boku 2. Przekątna graniastosłupa tworzy z jego podstawą kąt o mierze 60” (zobacz rysunek). Ń Wysokość tego graniastosłupa jest równa 4 B. 44/2 A A. c. | wś D. 246 prz ó 60


Zadanie 23. (0—1) Wszystkich czterocyfrowych liczb naturalnych, w których cyfra tysięcy i cyfra setek są większe od 4, a każda z pozostałych cyfr jest mniejsza od 6, jest A. 4:4.5-5 B. 5:4-:6:5 C. 5.:5.6:6 D. 4.3.5-4


Zadanie 24. (0—1) Wariancją zestawu czterech ocen z matematyki: 1, 3,5, 3, jest liczba A. I B. 2 c. 3


Zadanie 25. (0—1) W urnie jest 9 kul, w tym cztery kule czerwone, trzy zielone i dwie kule białe. Losujemy jedną kulę. Prawdopodobieństwo, że nie wylosowano ani kuli zielonej, ani białej, jest równe A. Ż B. > c. > p. * 5 9 9 9


Rozwiąż nierówność (2x+5)(3x-1)>0.

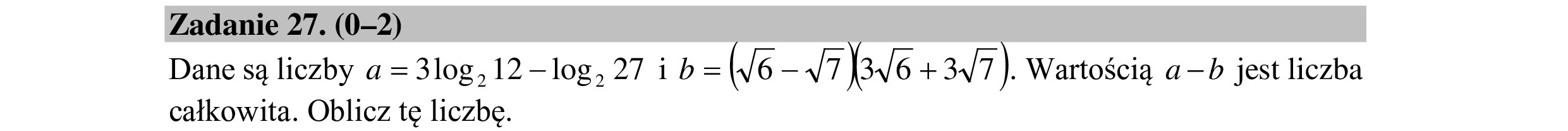
Zadanie 27. (0—2) Dane są liczby a = 3log, 12- log, 27 i b=(4/6-4T)BV6 + 34/7). Wartością a —b jest liczba całkowita. Oblicz tę liczbę.

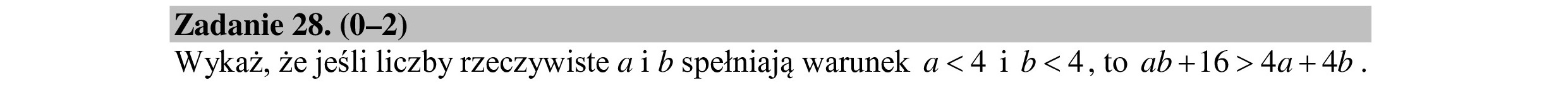
Zadanie 28. (0—2) Wykaż, że jeśli liczby rzeczywiste a i b spełniają warunek a<4 i b<4,to ab+16>4a+4b.


Zadanie 29. (0—2) Bok AB jest średnicą, a punkt S jest środkiem okręgu opisanego na trójkącie ABC. Punkt D leży na tym okręgu, a odcinek SD zawarty jest w symetralnej boku BC trójkąta (zobacz rysunek). Wykaż, że odcinek AD jest zawarty w dwusiecznej kąta CAB. KE

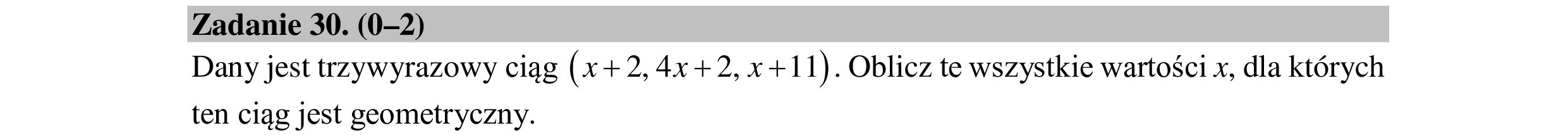
Zadanie 30. (0—2) Dany jest trzywyrazowy ciąg (x +2,4x+2,x+1 1) . Oblicz te wszystkie wartości x, dla których ten ciąg jest geometryczny.


Zadanie 31. (0—2) Prosta k jest nachylona do osi Ox pod kątem ostrym a, takim, że cosa= . Wyznacz »|śr współczynnik kierunkowy prostej k.

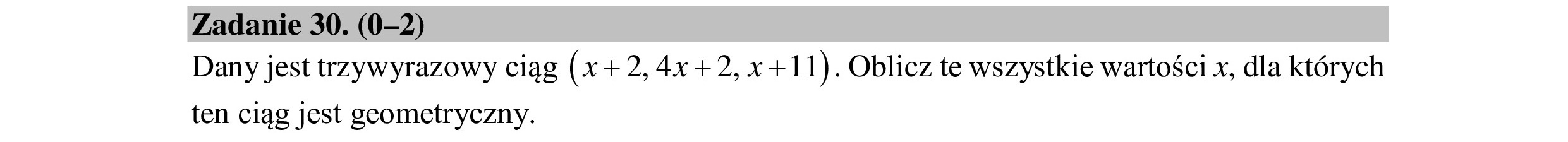
Zadanie 32. (0—4) Punkty A= (1-1) ,B= (6,1) „C= (7,5) i D= (2,4) są wierzchołkami czworokąta ABCD. Oblicz współrzędne punktu przecięcia przekątnych tego czworokąta.

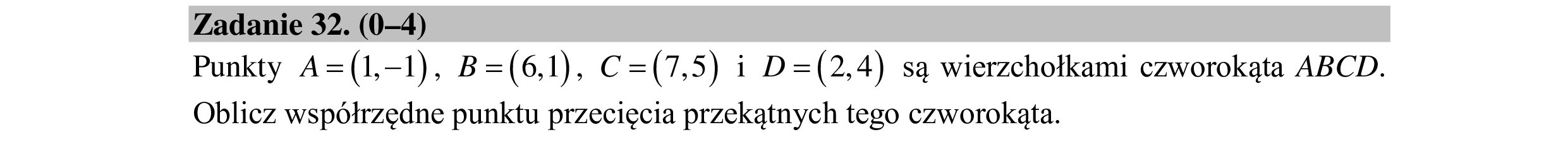
Zadanie 33. (0—4) Rzucamy cztery razy symetryczną monetą. Oblicz prawdopodobieństwo zdarzenia A, polegającego na tym, że liczba otrzymanych orłów będzie różna od liczby otrzymanych reszek.


Zadanie 34. (0—5) W ostrosłupie prawidłowym sześciokątnym ABCDEFS, którego krawędź podstawy a ma długość 8 (zobacz rysunek), ściana boczna jest nachylona do płaszczyzny podstawy pod kątem a =60”. Oblicz cosinus kąta między krawędzią boczną a płaszczyzną podstawy tego ostrosłupa. S






























