MATEMATYKA 2019 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) Liczba log ga7 jest równa A. 2 B. 7 c. N | —


Zadanie 2. (0—1) Kwadrat liczby 8— 347 jest równy A. 127+48J7 B. 127-4847 C. 1-487 D. 1+487

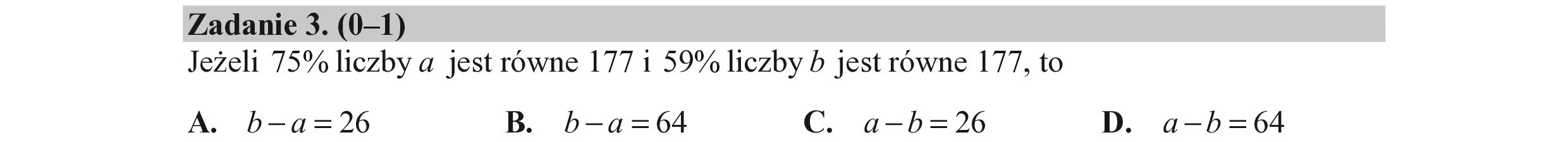
Zadanie 3. (0—1) Jeżeli 75% liczby a jest równe 177 i 59% liczby b jest równe 177, to A. b-a=26 B. b-a=64 C. a-b=2%6 D. a-b=64


Zadanie 4. (0—1) Równanie x(5x+1)=5x+1 ma dokładnie A. jedno rozwiązanie: x=l. B. dwa rozwiązania: x=l i x=—l1. . : 1. C. dwa rozwiązania: x=—— i x=l. D. dwa rozwiązania: x=— i x=—l1.


Zadanie 5. (0—1) RE -x+lży=a* Para liczb x=3 i y=l jest rozwiązaniem układu równań SDA dla 7 2x+ay=9 - A. a=— B. a=—-3 C. a=3 D. a=—— 3 3


Zadanie 6. (0—1) -—2 (u BJ(r+A] 0 madokładnie aaa (x- 4) B. jedno rozwiązanie: x =—2. , A. jedno rozwiązanie: x = 2. Równanie C. dwa rozwiązania: x = 2, x =—4. D. dwa rozwiązania: x = —2,x=4.

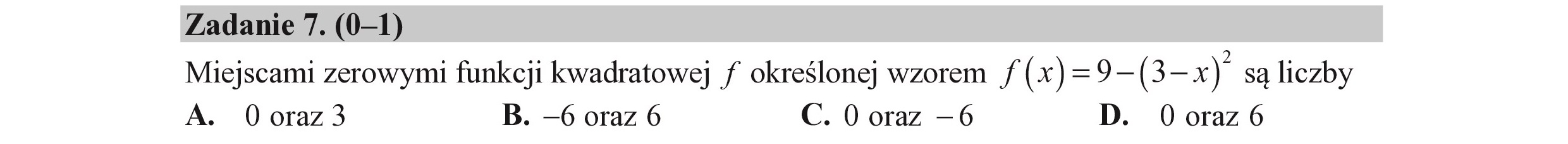
Zadanie 7. (0—1) Miejscami zerowymi funkcji kwadratowej / określonej wzorem /(x)=9— (3-x) są liczby A. 0 oraz 3 B. —6 oraz 6 C. 0 oraz —6 D. 0 oraz 6

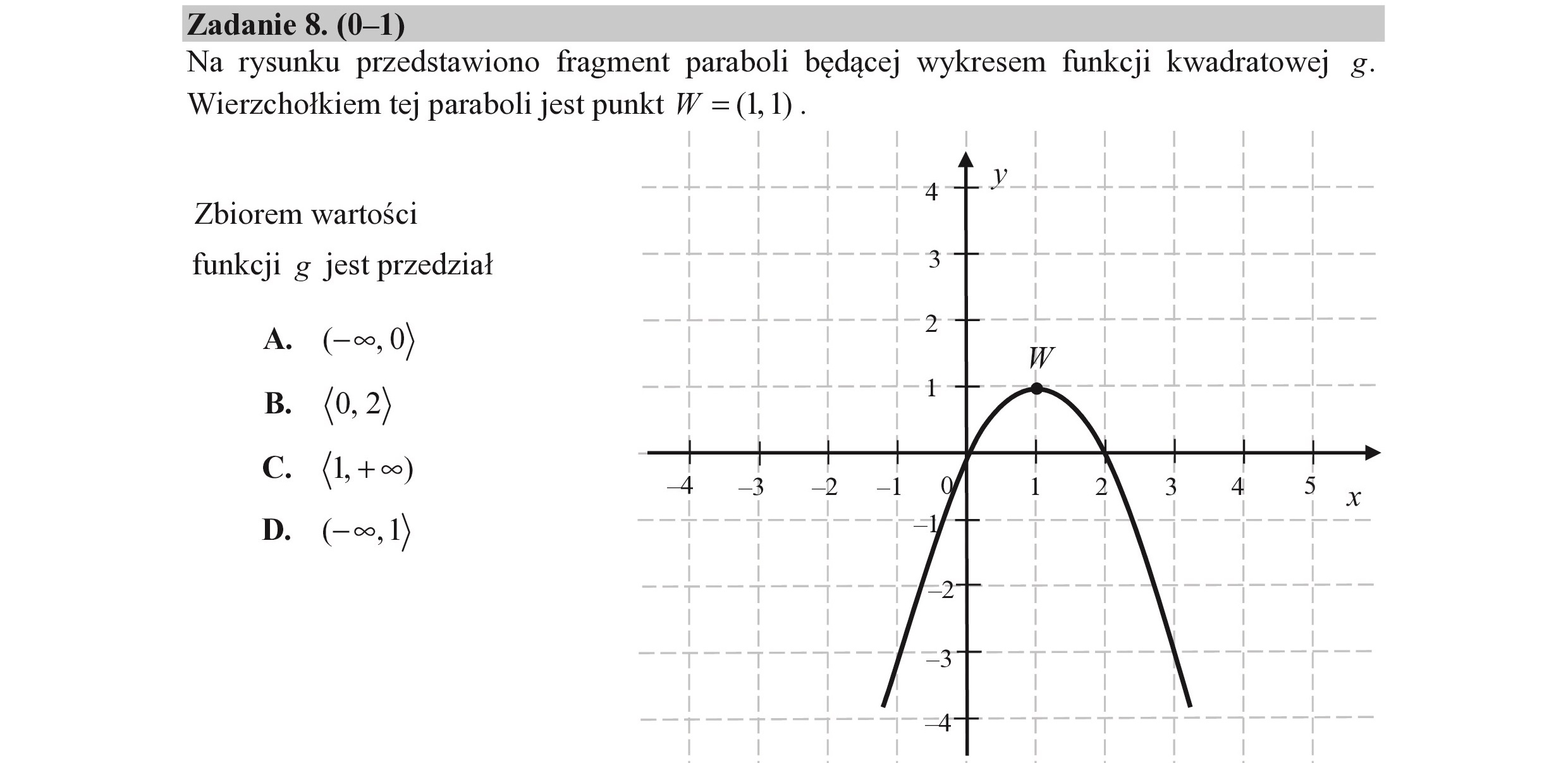
Zadanie 8. (0—1) Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej g. Wierzchołkiem tej paraboli jest punkt W =(1, 1). Zbiorem wartości funkcji g jest przedział A. (-0,0) B. (0,2) C. (1,+oo) D. (0,1)


Zadanie 9. (0—1) Liczbą większą od 5 jest 1 (5) 1)5 2 1 — Cc. 1253 D. 1253 25


Zadanie 10. (0—1) Punkt A=(a, 3) leży na prostej określonej równaniem y= ż» +6. Stąd wynika, że „Bł B. weż. 4 4 A. a=—4 B. a=4 C. a


Zadanie 11. (0—1) W ciągu arytmetycznym (a, ) , określonym dla n > 1, dane są dwa wyrazy: a, =-1li a, =5. Suma dziewięciu początkowych wyrazów tego ciągu jest równa A. —-24 B. -27 C. -16 D. -18


Zadanie 12. (0—1) Wszystkie wyrazy ciągu geometrycznego (a, ), określonego dla n > 1, są liczbami dodatnimi. Drugi wyraz tego ciągu jest równy 162, a piąty wyraz jest równy 48. Oznacza to, że iloraz tego ciągu jest równy 2 A. — B. EJ C. D 3 4 1 2 wW|-L

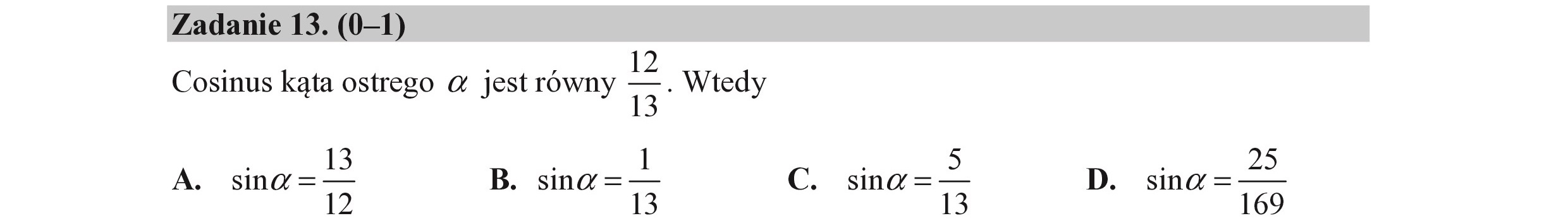
Zadanie 13. (0—1) Cosinus kąta ostrego a jest równy >: Wtedy A. sna= A B. sna = L 12 13 c. | 5 sina =— 3 D. . 23 sina =—— 169

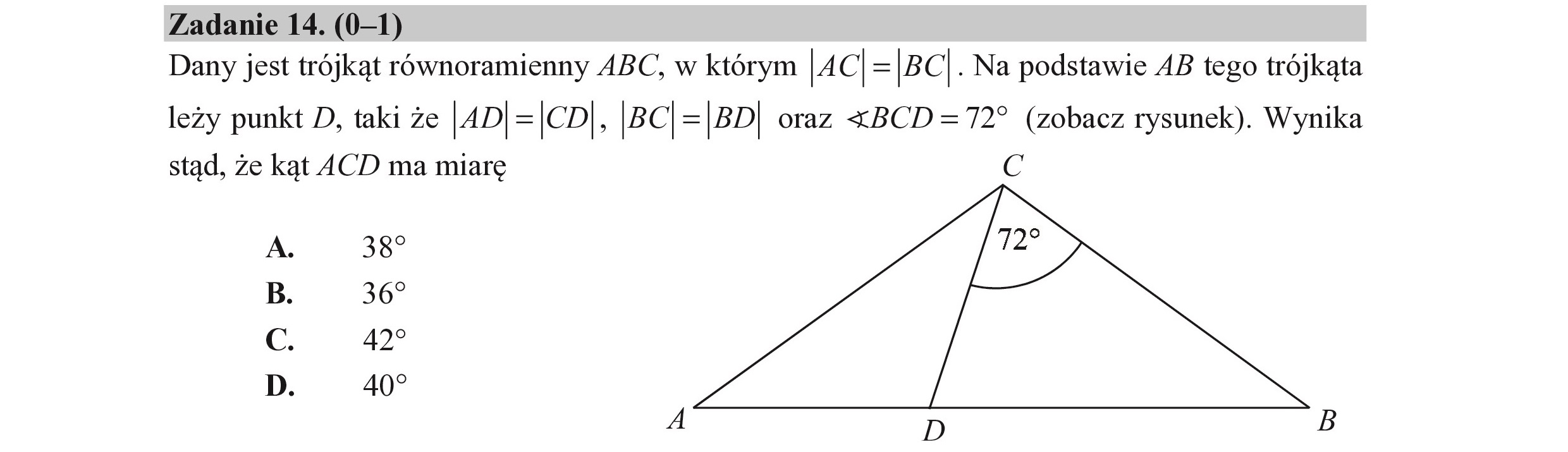
Zadanie 14. (0—1) Dany jest trójkąt równoramienny ABC, w którym AC = |BC| . Na podstawie AB tego trójkąta leży punkt D, taki że |4D|=|CD stąd, że kąt ACD ma miarę SOP 38 367 427 40 z BC | =|BD| oraz «BCD=72* (zobacz rysunek). Wynika C |e>


Zadanie 15. (0—1) Okrąg, którego środkiem jest punkt S$ =(a,5), jest styczny do osi Oy i do prostej o równaniu y=2. Promień tego okręgu jest równy A. 3 B. 5 c 2 D. 4

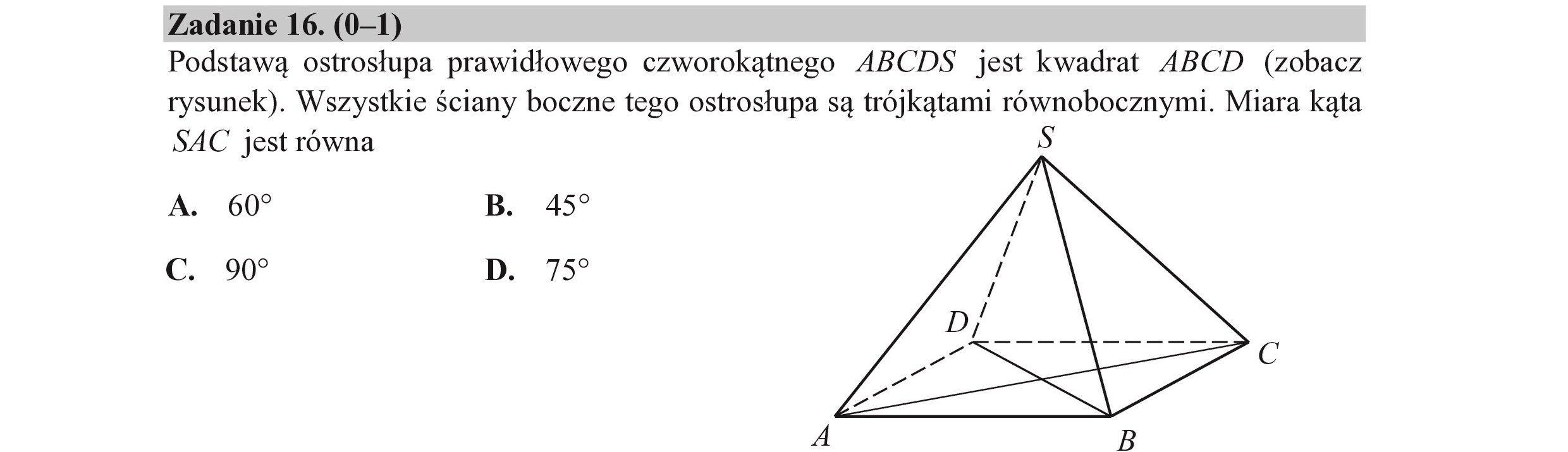
Zadanie 16. (0—1) Podstawą ostrosłupa prawidłowego czworokątnego ABCDS jest kwadrat ABCD (zobacz rysunek). Wszystkie Ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta SAC jest równa A. 60? B. 459 c. 90” D. 759 Za WŃ i A B

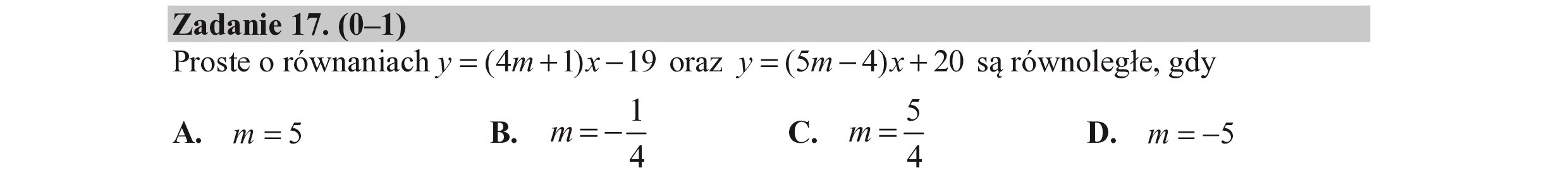
Zadanie 17. (0—1) Proste o równaniach y = (4m + 1)x —19 oraz y=(5m—4)x+ 20 są równoległe, gdy 1 5 A. m=$5 B. m=—— Cc. m=— D. m=-5 4 4


Zadanie 18. (0—1) W układzie współrzędnych punkt S=(40, 40) jest środkiem odcinka KZ, którego jednym z końców jest punkt K =(0,8). Zatem A. L=(20,24) B. L=(-80,—72) C. L=(-40,—24) D. L=(80,72)


Zadanie 19. (0—1) Punkt P=(-6,—8), przekształcono najpierw w symetrii względem osi Ox, a potem w symetrii względem osi Qy. W wyniku tych przekształceń otrzymano punkt O . Zatem A. Q=(6,8) B. Q=(—6,—8) c. 0Q0=(8,6) D. Q=(-8,—6)


Zadanie 20. (0—1) W układzie współrzędnych na płaszczyźnie danych jest 5 punktów: 4=(1,4), B=(-5,—1), C=(-5,3), D=(6,—4), P=(-30, -76). Punkt P należy do tej samej ćwiartki układu współrzędnych co punkt A. A B. 5 GC D. D

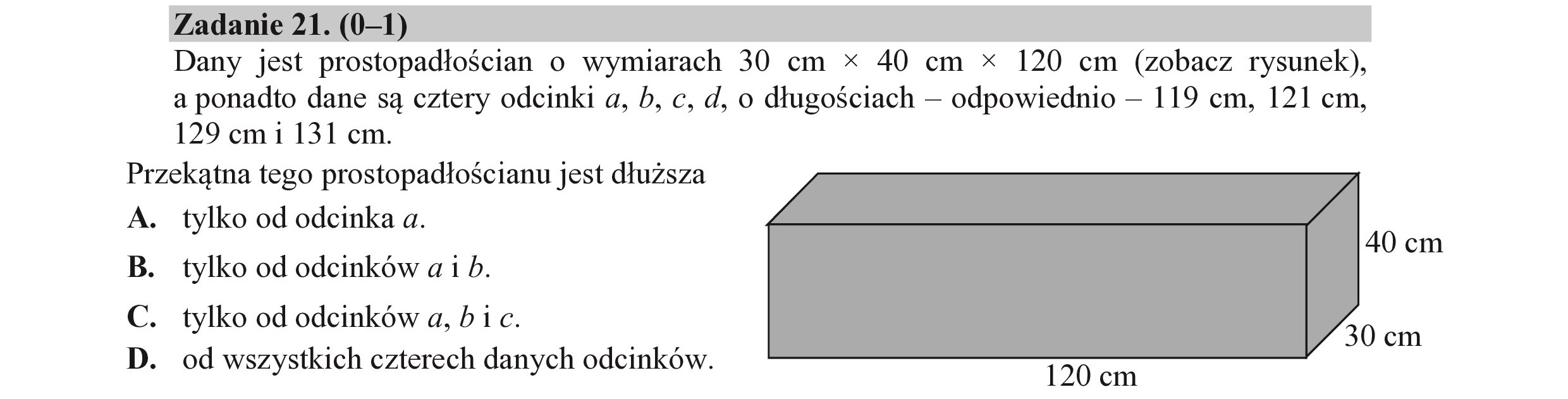
Przekątna tego prostopadłościanu jest dłuższa A. B. GC D Zadanie 21. (0-1) Dany jest prostopadłościan o wymiarach 30 cm x 40 cm * 120 cm (zobacz rysunek), a ponadto dane są cztery odcinki a, b, c, d, o długościach — odpowiednio — 119 cm, 121 cm, 129 cm i 131 cm. tylko od odcinka a. tylko od odcinków a ib. tylko od odcinków a, bic. od wszystkich czterech danych odcinków. 40 cm 30 cm 120 cm


Zadanie 22. (0-1) Pole powierzchni całkowitej pewnego stożka jest 3 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 2 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą A. 12 B. Il Cc. 24 D. 22


Zadanie 23. (0—1) Srednia arytmetyczna dziesięciu liczb naturalnych 3, 10, 5, x, x, x, x, 12, 19, 7 jest równa 12. Mediana tych liczb jest równa A. 14 B. 12 C. 16 D. x


Zadanie 24. (0—1) Wszystkich liczb naturalnych czterocyfrowych parzystych, w których występują wyłącznie cyfry 1, 2, 3, jest A. 54 B. 81 c. 8 D. 27


Zadanie 25. (0—1) W grupie 60 osób (kobiet i mężczyzn) jest 35 kobiet. Z tej grupy losujemy jedną osobę. Prawdopodobieństwo wylosowania każdej osoby jest takie samo. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy mężczyznę, jest równe l B l Cc 7 5 A. — — SE . 60 25 12 12


Zadanie 26. (0—2) Rozwiąż równanie (x — 16) (x — 1) =),


Zadanie 27. (0-2) Rozwiąż nierówność 2x —5x+3<0.


Zadanie 28. (0—2) Wykaż, że dla każdej liczby dodatniej x prawdziwa jest nierówność x ać > l. x

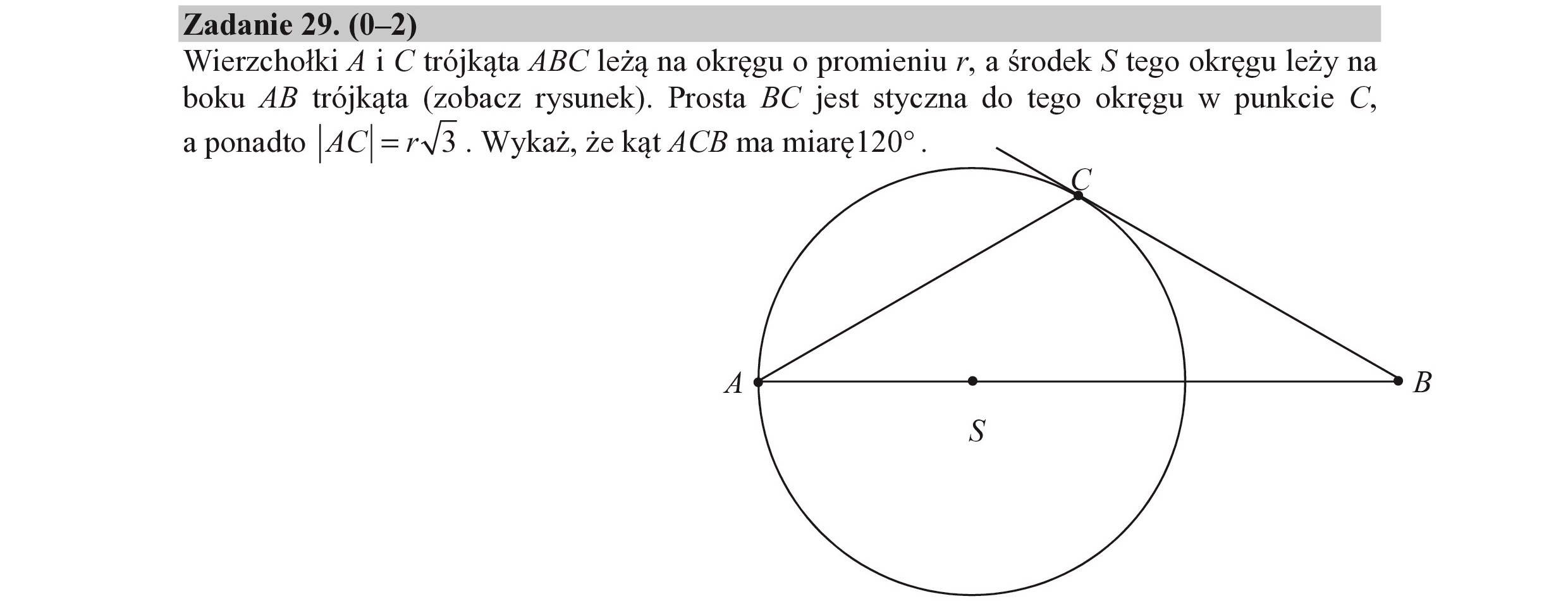
Zadanie 29. (0-2) Wierzchołki A i C trójkąta ABC leżą na okręgu o promieniu 7, a środek $ tego okręgu leży na boku AB trójkąta (zobacz rysunek). Prosta BC jest styczna do tego okręgu w punkcie C, a ponadto |AC| =r43. Wykaż, że kąt ACB ma miaręl1207.


Zadanie 30. (0—2) Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru 41,3,5,7,9), i jednocześnie cyfrę jedności, która należy do zbioru 10, 2, 4,6,8].


Zadanie 31. (0-2) 21 Przekątne rombu ABCD przecinają się w punkcie S$ -|-2-1). Punkty A i C leżą na "= ; 1 5 ; : s prostej o równaniu y= z” + g' Wyznacz równanie prostej BD.


Zadanie 32. (0—4) W ciągu arytmetycznym (a,,a,,..,a,,d,) suma wyrazów tego ciągu o numerach parzystych jest równa 1340, a suma wyrazów ciągu o numerach nieparzystych jest równa 1400. Wyznacz ostatni wyraz tego ciągu arytmetycznego.


Zadanie 33. (0—4) Srodek okręgu leży w odległości 10 cm od cięciwy tego okręgu. Długość tej cięciwy jest o 22 cm większa od promienia tego okręgu. Oblicz promień tego okręgu.

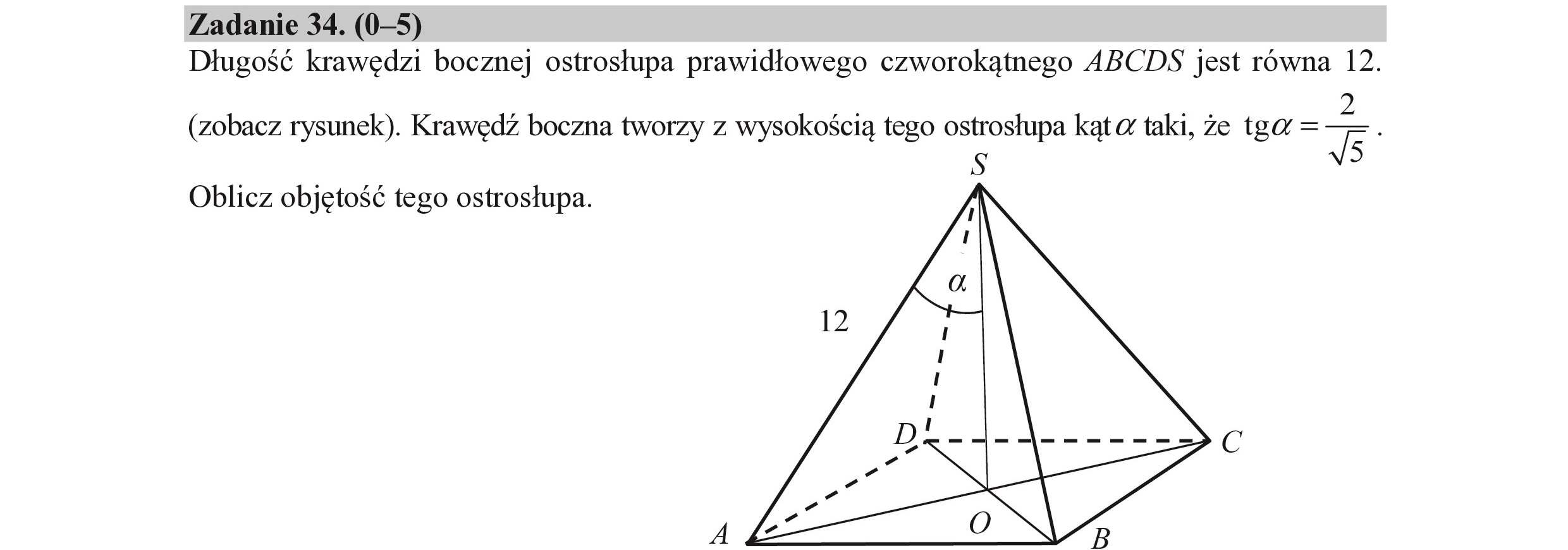
Zadanie 34. (0—5) Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego ABCDS jest równa 12. : ! p. (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąta: taki, że tga = 6 . S Oblicz objętość tego ostrosłupa. zac za

MATEMATYKA 2019 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) Liczba log ga7 jest równa A. 2 B. 7 c. N | —


Zadanie 2. (0—1) Kwadrat liczby 8— 347 jest równy A. 127+48J7 B. 127-4847 C. 1-487 D. 1+487

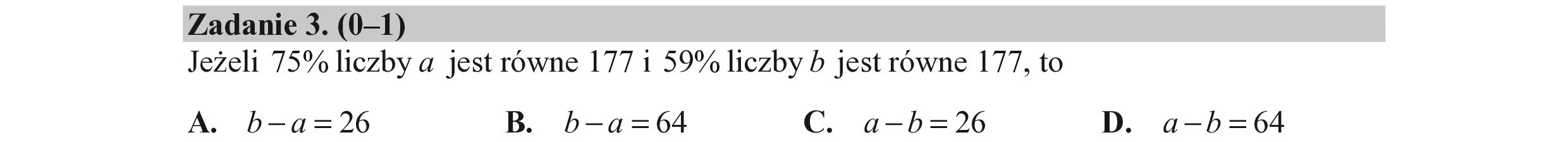
Zadanie 3. (0—1) Jeżeli 75% liczby a jest równe 177 i 59% liczby b jest równe 177, to A. b-a=26 B. b-a=64 C. a-b=2%6 D. a-b=64


Zadanie 4. (0—1) Równanie x(5x+1)=5x+1 ma dokładnie A. jedno rozwiązanie: x=l. B. dwa rozwiązania: x=l i x=—l1. . : 1. C. dwa rozwiązania: x=—— i x=l. D. dwa rozwiązania: x=— i x=—l1.


Zadanie 5. (0—1) RE -x+lży=a* Para liczb x=3 i y=l jest rozwiązaniem układu równań SDA dla 7 2x+ay=9 - A. a=— B. a=—-3 C. a=3 D. a=—— 3 3


Zadanie 6. (0—1) -—2 (u BJ(r+A] 0 madokładnie aaa (x- 4) B. jedno rozwiązanie: x =—2. , A. jedno rozwiązanie: x = 2. Równanie C. dwa rozwiązania: x = 2, x =—4. D. dwa rozwiązania: x = —2,x=4.

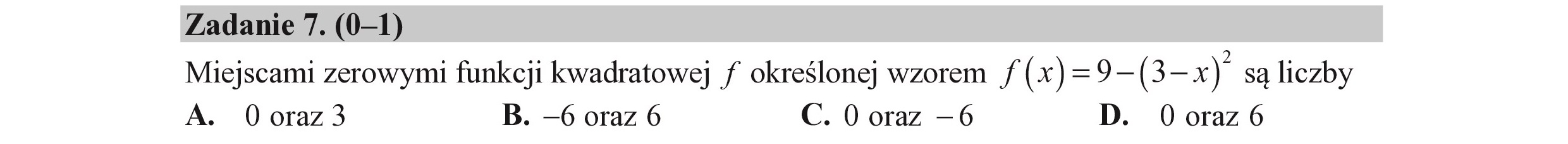
Zadanie 7. (0—1) Miejscami zerowymi funkcji kwadratowej / określonej wzorem /(x)=9— (3-x) są liczby A. 0 oraz 3 B. —6 oraz 6 C. 0 oraz —6 D. 0 oraz 6


Zadanie 8. (0—1) Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej g. Wierzchołkiem tej paraboli jest punkt W =(1, 1). Zbiorem wartości funkcji g jest przedział A. (-0,0) B. (0,2) C. (1,+oo) D. (0,1)


Zadanie 9. (0—1) Liczbą większą od 5 jest 1 (5) 1)5 2 1 — Cc. 1253 D. 1253 25


Zadanie 10. (0—1) Punkt A=(a, 3) leży na prostej określonej równaniem y= ż» +6. Stąd wynika, że „Bł B. weż. 4 4 A. a=—4 B. a=4 C. a


Zadanie 11. (0—1) W ciągu arytmetycznym (a, ) , określonym dla n > 1, dane są dwa wyrazy: a, =-1li a, =5. Suma dziewięciu początkowych wyrazów tego ciągu jest równa A. —-24 B. -27 C. -16 D. -18


Zadanie 12. (0—1) Wszystkie wyrazy ciągu geometrycznego (a, ), określonego dla n > 1, są liczbami dodatnimi. Drugi wyraz tego ciągu jest równy 162, a piąty wyraz jest równy 48. Oznacza to, że iloraz tego ciągu jest równy 2 A. — B. EJ C. D 3 4 1 2 wW|-L

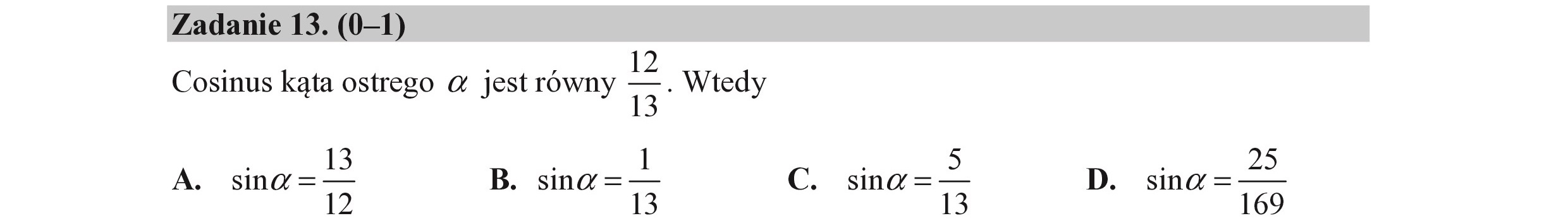
Zadanie 13. (0—1) Cosinus kąta ostrego a jest równy >: Wtedy A. sna= A B. sna = L 12 13 c. | 5 sina =— 3 D. . 23 sina =—— 169


Zadanie 14. (0—1) Dany jest trójkąt równoramienny ABC, w którym AC = |BC| . Na podstawie AB tego trójkąta leży punkt D, taki że |4D|=|CD stąd, że kąt ACD ma miarę SOP 38 367 427 40 z BC | =|BD| oraz «BCD=72* (zobacz rysunek). Wynika C |e>


Zadanie 15. (0—1) Okrąg, którego środkiem jest punkt S$ =(a,5), jest styczny do osi Oy i do prostej o równaniu y=2. Promień tego okręgu jest równy A. 3 B. 5 c 2 D. 4


Zadanie 16. (0—1) Podstawą ostrosłupa prawidłowego czworokątnego ABCDS jest kwadrat ABCD (zobacz rysunek). Wszystkie Ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta SAC jest równa A. 60? B. 459 c. 90” D. 759 Za WŃ i A B

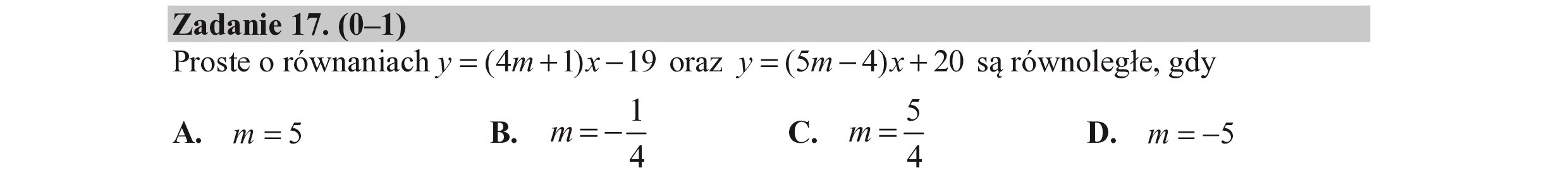
Zadanie 17. (0—1) Proste o równaniach y = (4m + 1)x —19 oraz y=(5m—4)x+ 20 są równoległe, gdy 1 5 A. m=$5 B. m=—— Cc. m=— D. m=-5 4 4


Zadanie 18. (0—1) W układzie współrzędnych punkt S=(40, 40) jest środkiem odcinka KZ, którego jednym z końców jest punkt K =(0,8). Zatem A. L=(20,24) B. L=(-80,—72) C. L=(-40,—24) D. L=(80,72)


Zadanie 19. (0—1) Punkt P=(-6,—8), przekształcono najpierw w symetrii względem osi Ox, a potem w symetrii względem osi Qy. W wyniku tych przekształceń otrzymano punkt O . Zatem A. Q=(6,8) B. Q=(—6,—8) c. 0Q0=(8,6) D. Q=(-8,—6)


Zadanie 20. (0—1) W układzie współrzędnych na płaszczyźnie danych jest 5 punktów: 4=(1,4), B=(-5,—1), C=(-5,3), D=(6,—4), P=(-30, -76). Punkt P należy do tej samej ćwiartki układu współrzędnych co punkt A. A B. 5 GC D. D


Przekątna tego prostopadłościanu jest dłuższa A. B. GC D Zadanie 21. (0-1) Dany jest prostopadłościan o wymiarach 30 cm x 40 cm * 120 cm (zobacz rysunek), a ponadto dane są cztery odcinki a, b, c, d, o długościach — odpowiednio — 119 cm, 121 cm, 129 cm i 131 cm. tylko od odcinka a. tylko od odcinków a ib. tylko od odcinków a, bic. od wszystkich czterech danych odcinków. 40 cm 30 cm 120 cm


Zadanie 22. (0-1) Pole powierzchni całkowitej pewnego stożka jest 3 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 2 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą A. 12 B. Il Cc. 24 D. 22


Zadanie 23. (0—1) Srednia arytmetyczna dziesięciu liczb naturalnych 3, 10, 5, x, x, x, x, 12, 19, 7 jest równa 12. Mediana tych liczb jest równa A. 14 B. 12 C. 16 D. x


Zadanie 24. (0—1) Wszystkich liczb naturalnych czterocyfrowych parzystych, w których występują wyłącznie cyfry 1, 2, 3, jest A. 54 B. 81 c. 8 D. 27


Zadanie 25. (0—1) W grupie 60 osób (kobiet i mężczyzn) jest 35 kobiet. Z tej grupy losujemy jedną osobę. Prawdopodobieństwo wylosowania każdej osoby jest takie samo. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy mężczyznę, jest równe l B l Cc 7 5 A. — — SE . 60 25 12 12


Zadanie 26. (0—2) Rozwiąż równanie (x — 16) (x — 1) =),


Zadanie 27. (0-2) Rozwiąż nierówność 2x —5x+3<0.


Zadanie 28. (0—2) Wykaż, że dla każdej liczby dodatniej x prawdziwa jest nierówność x ać > l. x


Zadanie 29. (0-2) Wierzchołki A i C trójkąta ABC leżą na okręgu o promieniu 7, a środek $ tego okręgu leży na boku AB trójkąta (zobacz rysunek). Prosta BC jest styczna do tego okręgu w punkcie C, a ponadto |AC| =r43. Wykaż, że kąt ACB ma miaręl1207.


Zadanie 30. (0—2) Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru 41,3,5,7,9), i jednocześnie cyfrę jedności, która należy do zbioru 10, 2, 4,6,8].


Zadanie 31. (0-2) 21 Przekątne rombu ABCD przecinają się w punkcie S$ -|-2-1). Punkty A i C leżą na "= ; 1 5 ; : s prostej o równaniu y= z” + g' Wyznacz równanie prostej BD.


Zadanie 32. (0—4) W ciągu arytmetycznym (a,,a,,..,a,,d,) suma wyrazów tego ciągu o numerach parzystych jest równa 1340, a suma wyrazów ciągu o numerach nieparzystych jest równa 1400. Wyznacz ostatni wyraz tego ciągu arytmetycznego.


Zadanie 33. (0—4) Srodek okręgu leży w odległości 10 cm od cięciwy tego okręgu. Długość tej cięciwy jest o 22 cm większa od promienia tego okręgu. Oblicz promień tego okręgu.


Zadanie 34. (0—5) Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego ABCDS jest równa 12. : ! p. (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąta: taki, że tga = 6 . S Oblicz objętość tego ostrosłupa. zac za






























