MATEMATYKA 2018 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) Cena pewnego towaru w wyniku obniżki o 10% zmniejszyła się o 2 018 zł. Ten towar po tej obniżce kosztował A. 20 180zł B. 18 l62zł C. 2108 zł D. 2028 zł


Liczba NR/2 jest równa > N G w NN e) NN w| *|N

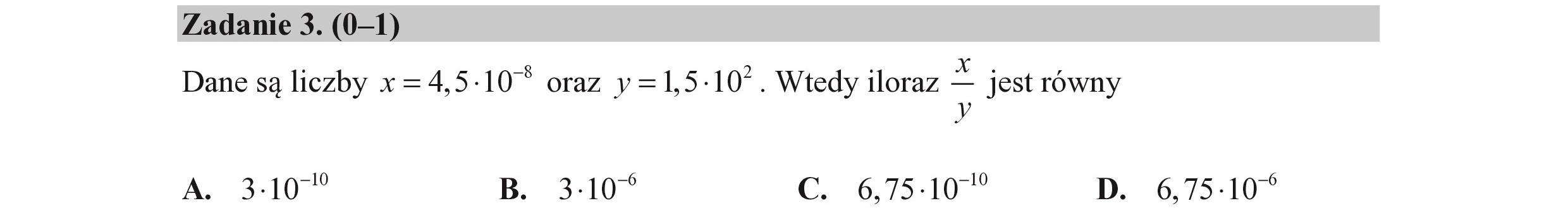
Zadanie 3. (0—1) Dane są liczby x =4,5-10* oraz y=1,5:10”. Wtedy iloraz — jest równy P A. 3:10 B. 3-:10% C. 6,75-10" D. 6,75-10*


Zadanie 4. (0—1) Liczba log, 96— log, 6 jest równa A. log, 90 B. log,96


Zadanie 5. (0—1) 2 Równość (a +24/3 | =13+44/3 jest prawdziwa dla A. a=AI3 B. a=l C. a=0 D. a=AMI3+1


Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi x 1 y. Zadanie 6. (0—1) Wskaż ten układ. =IRRI-GE rów NSS Em 2 =iZRI-ÓRE ró0E TRE BiT R - --1---+--4---+4-— sousalaczew bozia dba wóóa w 1 1 1 1 1 1 zma lm sm KME p 1 >| + > —| | II A y=2x-4 » | —2x+8 +


Zadanie 7. (0—1) Rozwiązaniem równania A. 2 — No) jest liczba


Zadanie 8. (0—1) Dane są funkcje f(x)=3" oraz g(x)=f(-x), określone dla wszystkich liczb rzeczywistych x. Punkt wspólny wykresów funkcji /f ig A. nie istnieje. B. ma współrzędne (1,0). C. ma współrzędne (0, 1). D. ma współrzędne (0,0).

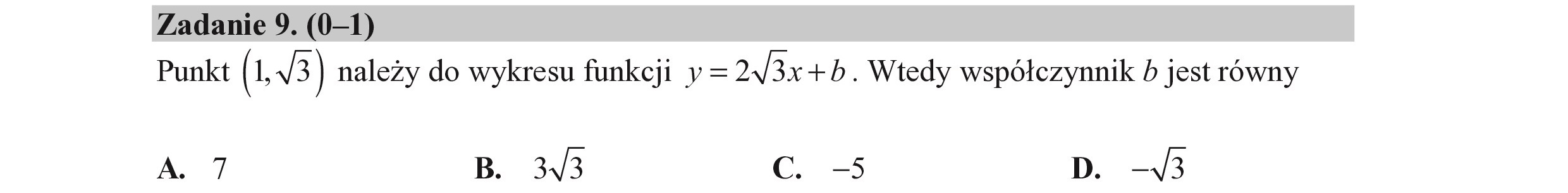
Zadanie 9. (0—1) Punkt (1 3 | należy do wykresu funkcji y= 243x+b. Wtedy współczynnik b jest równy A. 7 B. 3/3 C. -5 D. -133

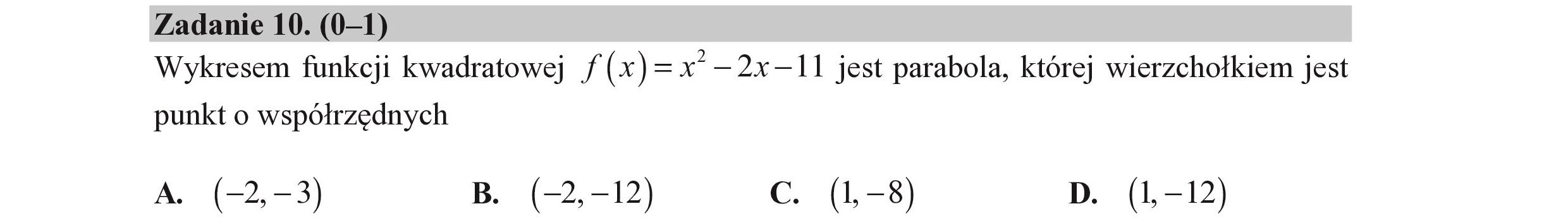
Zadanie 10. (0—1) Wykresem funkcji kwadratowej /(x)= x —2x—11 jest parabola, której wierzchołkiem jest punkt o współrzędnych A. (-2,—3) B. (-2,—12) Cc. (1,-8) D. (1-12)


Zadanie 11. (0—1) Funkcja kwadratowa jest określona wzorem /(x)=—3(x-2)(x—9). Liczby x, x, różnymi miejscami zerowymi funkcji f. Zatem A. x+x,=l1I B x+x=-11 C. x+x,=33 D. x+x, =—33 są


Zadanie 12. (0—1) Największą wartością funkcji y = -(x-2) +4 w przedziale (3, 5) jest A. 0 B. 5 C. 4 D. 3


Zadanie 13. (0—1) Ciąg arytmetyczny (a, ), określony dla n > 1, spełnia warunek a, +a, +a, =15. Wtedy A. a,=5 B. a,=6 C. a,=3 D. a,=4


Zadanie 14. (0—1) Dla pewnej liczby x ciąg (x, x + 4,16) jest geometryczny. Liczba x jest równa A. 8 B. 4 Cc 2 D. 0


Zadanie 15. (0—1) W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta a jest równa „3 . Zatem A. a=609 B. 2e(40,60) CC. ae(30,409) D. a=309

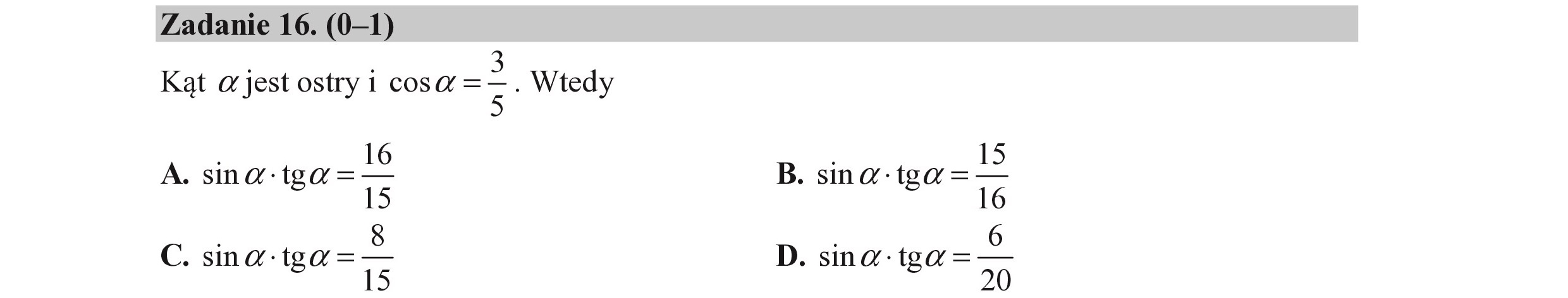
Zadanie 16. (0—1) Kąt a jest ostry i cosa = > „ Wtedy A. sina-1g0=-3 B. sina-1g0= > C. sna:tga =— D. śnardgir=""- JE 20

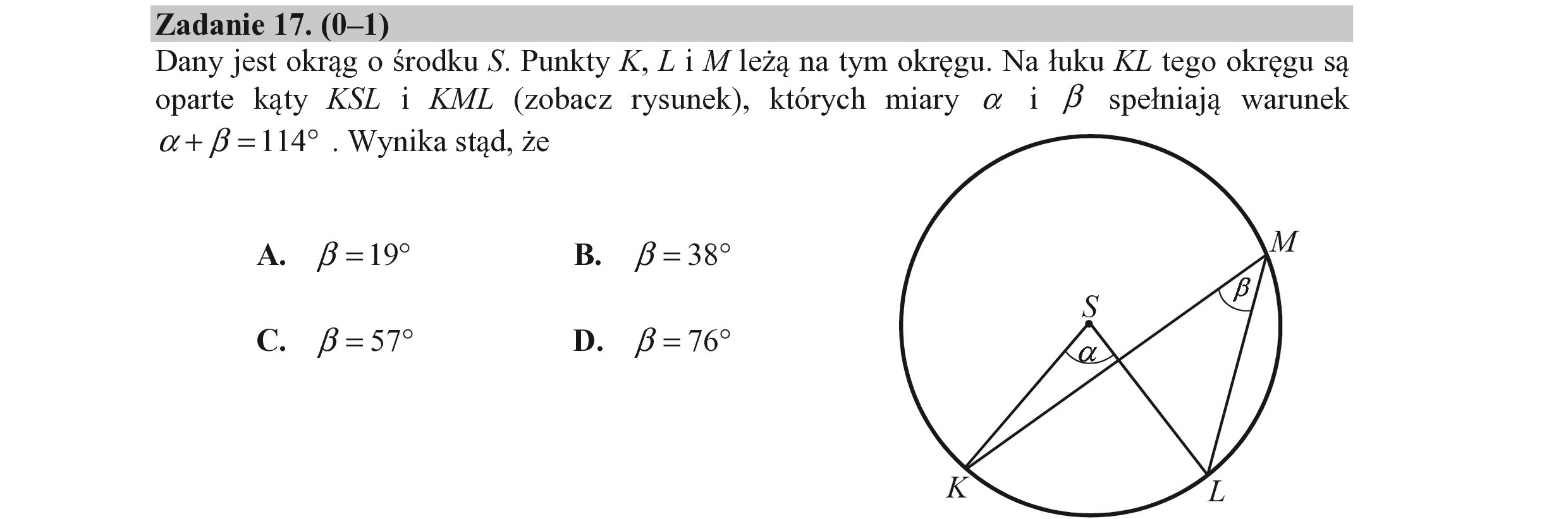
Zadanie 17. (0—1) Dany jest okrąg o środku 5. Punkty K, Z 1 M leżą na tym okręgu. Na łuku KZ tego okręgu są oparte kąty KSZ i KML (zobacz rysunek), których miary a i 8 spełniają warunek a+]B=114* . Wynika stąd, że A. B=19 B. 8=389 C. 8=57 D. 8=76


Zadanie 18. (0—1) Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 80”. Kąt rozwarty tego równoległoboku ma miarę A. 120? B. 1257 c. 130? D. 135?


Zadanie 19. (0—1) Pole trójkąta o bokach długości 4 oraz 9 i kącie między nimi o mierze 60” jest równe A. 18 B. 9 C. 18/3 D. 93


Zadanie 20. (0—1) Proste o równaniach y=(3m—4)x+2 oraz y=(12—m)x+3m są równoległe, gdy A. m=4 B. m=3 C. m=—4 D. m=—-3


Zadanie 21. (0—1) Punkt A=(—3,2) jest końcem odcinka 4B, a punkt M =(4,1) jest środkiem tego odcinka. Długość odcinka AB jest równa A. 245 B. 4/5 Cc. 542 D. 1042


Zadanie 22. (0—1) Jeżeli © oznacza miarę kąta między przekątną sześcianu a przekątną Ściany bocznej tego sześcianu (zobacz rysunek), to (NIZA A. sina= 46 B. sina= 2 3 2 C. sina= = D. sna= 8


Zadanie 23. (0-1) Przekrój osiowy walca jest kwadratem o przekątnej 10/2. Pole powierzchni bocznej tego walca jest równe A. 50m B. 100m c. 200m D. 250n

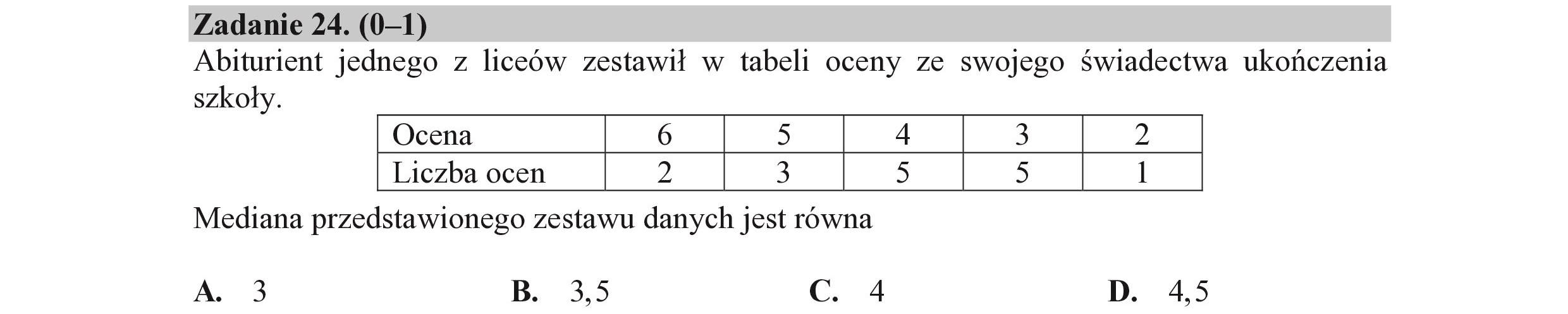
Zadanie 24. (0—1) Abiturient jednego z liceów zestawił w tabeli oceny ze swojego Świadectwa ukończenia szkoły. Ocena 6 5 4 3 2 Mediana przedstawionego zestawu danych jest równa A. 3 B. 3,5 C. 4 D. 4,5


Zadanie 25. (0—1) W grupie liczącej 29 uczniów (dziewcząt i chłopców) jest 15 chłopców. Z. tej grupy trzeba wylosować jedną osobę. Prawdopodobieństwo zdarzenia polegającego na tym, że zostanie wylosowana dziewczyna, jest równe = B. — a > D. > 15 14 29 29


Zadanie 26. (0-2) Rozwiąż nierówność x +óx-16<0.


Zadanie 27. (0—2) Rozwiąż równanie (2 + 27) (x — 16) = (b

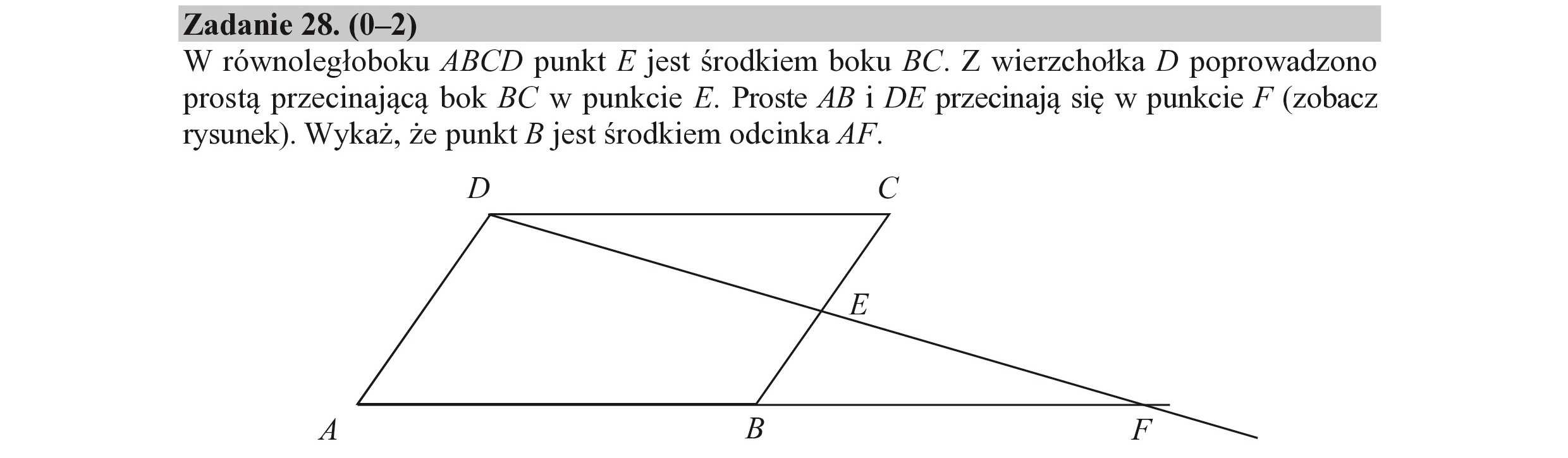
Zadanie 28. (0—2) W równoległoboku ABCD punkt £ jest środkiem boku BC. Z wierzchołka D poprowadzono prostą przecinającą bok BC w punkcie E. Proste AB i DE przecinają się w punkcie / (zobacz rysunek). Wykaż, że punkt B jest środkiem odcinka AF. JE, >


Zadanie 29. (0—2) Wykaż, że jeżeli a i b są liczbami rzeczywistymi dodatnimi, to (a+ (23 z 24. a


Zadanie 30. (0—2) Dziewiąty wyraz ciągu arytmetycznego (a, ), określonego dla n>1, jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.


Zadanie 31. (0—2) Punkty A=(2,4), B=(0,0), C=(4,—2) są wierzchołkami trójkąta ABC. Punkt D jest środkiem boku AC tego trójkąta. Wyznacz równanie prostej BD.

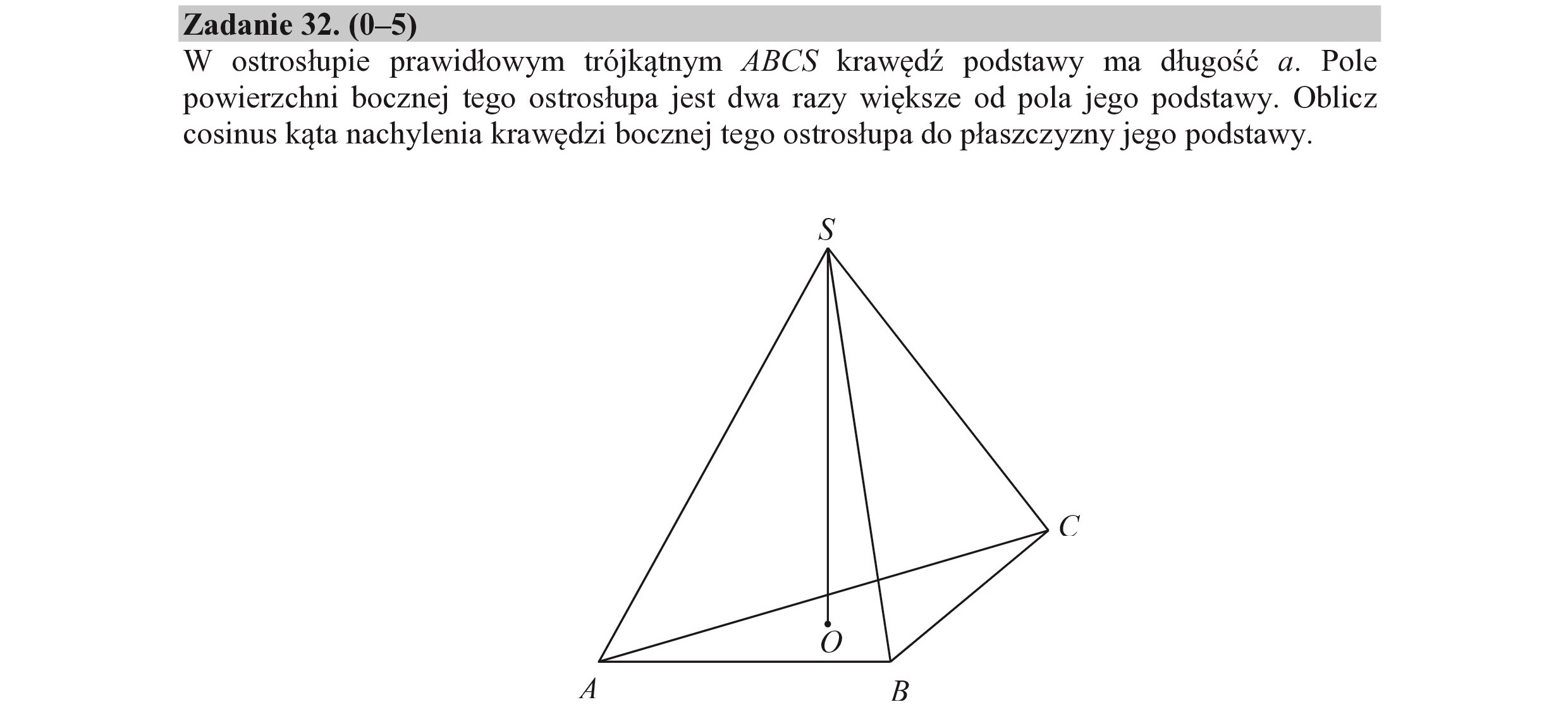
Zadanie 32. (0—5) W ostrosłupie prawidłowym trójkątnym ABCS krawędź podstawy ma długość a. Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy. (6 |


Zadanie 33. (0—4) Ze zbioru A=[-3,—2,—1,1,2,3| losujemy liczbę a, natomiast ze zbioru B= -1,0, 1, 2) losujemy liczbę b. Te liczby są — odpowiednio — współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej f (x) =ax+b. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja / jest rosnąca i ma dodatnie miejsce zerowe.


Zadanie 34. (0—4) W trójkącie prostokątnym ACB przyprostokątna AC ma długość 5, a promień okręgu wpisanego w ten trójkąt jest równy 2. Oblicz pole trójkąta ACB.

MATEMATYKA 2018 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) Cena pewnego towaru w wyniku obniżki o 10% zmniejszyła się o 2 018 zł. Ten towar po tej obniżce kosztował A. 20 180zł B. 18 l62zł C. 2108 zł D. 2028 zł


Liczba NR/2 jest równa > N G w NN e) NN w| *|N

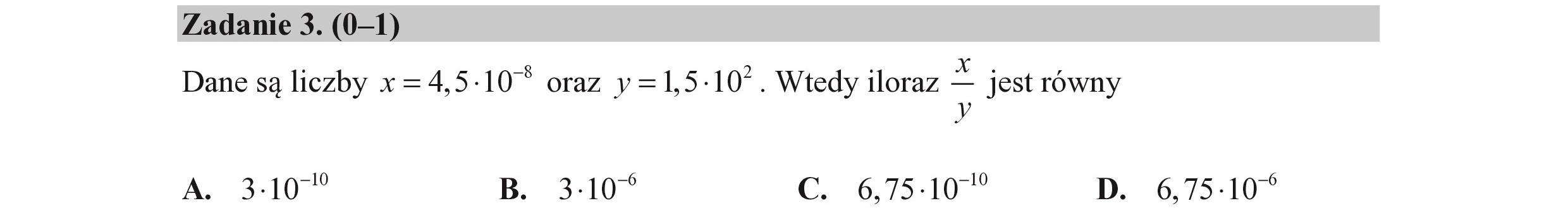
Zadanie 3. (0—1) Dane są liczby x =4,5-10* oraz y=1,5:10”. Wtedy iloraz — jest równy P A. 3:10 B. 3-:10% C. 6,75-10" D. 6,75-10*


Zadanie 4. (0—1) Liczba log, 96— log, 6 jest równa A. log, 90 B. log,96


Zadanie 5. (0—1) 2 Równość (a +24/3 | =13+44/3 jest prawdziwa dla A. a=AI3 B. a=l C. a=0 D. a=AMI3+1


Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi x 1 y. Zadanie 6. (0—1) Wskaż ten układ. =IRRI-GE rów NSS Em 2 =iZRI-ÓRE ró0E TRE BiT R - --1---+--4---+4-— sousalaczew bozia dba wóóa w 1 1 1 1 1 1 zma lm sm KME p 1 >| + > —| | II A y=2x-4 » | —2x+8 +


Zadanie 7. (0—1) Rozwiązaniem równania A. 2 — No) jest liczba


Zadanie 8. (0—1) Dane są funkcje f(x)=3" oraz g(x)=f(-x), określone dla wszystkich liczb rzeczywistych x. Punkt wspólny wykresów funkcji /f ig A. nie istnieje. B. ma współrzędne (1,0). C. ma współrzędne (0, 1). D. ma współrzędne (0,0).

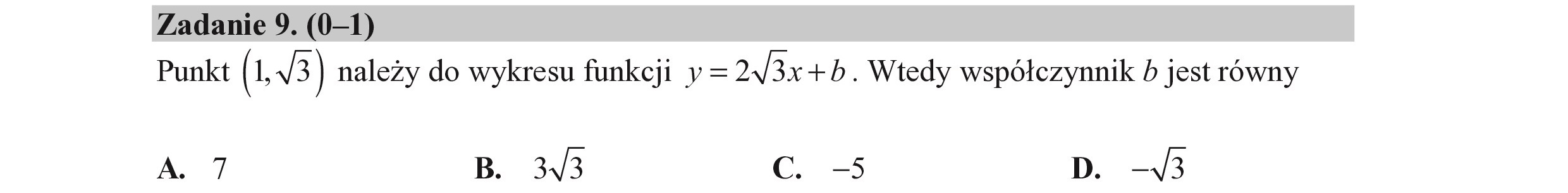
Zadanie 9. (0—1) Punkt (1 3 | należy do wykresu funkcji y= 243x+b. Wtedy współczynnik b jest równy A. 7 B. 3/3 C. -5 D. -133

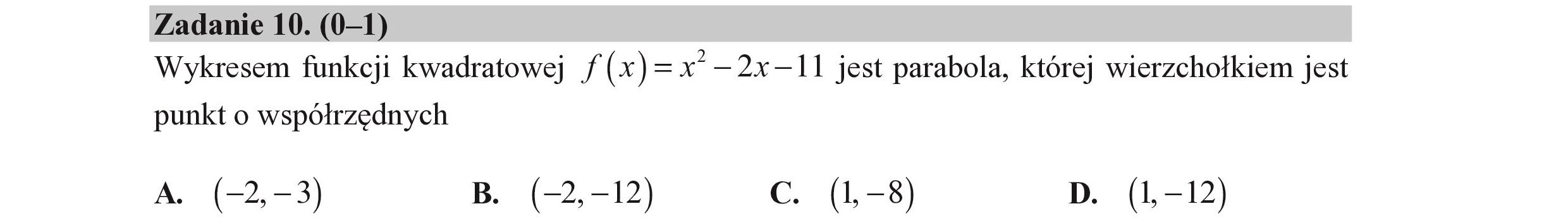
Zadanie 10. (0—1) Wykresem funkcji kwadratowej /(x)= x —2x—11 jest parabola, której wierzchołkiem jest punkt o współrzędnych A. (-2,—3) B. (-2,—12) Cc. (1,-8) D. (1-12)


Zadanie 11. (0—1) Funkcja kwadratowa jest określona wzorem /(x)=—3(x-2)(x—9). Liczby x, x, różnymi miejscami zerowymi funkcji f. Zatem A. x+x,=l1I B x+x=-11 C. x+x,=33 D. x+x, =—33 są


Zadanie 12. (0—1) Największą wartością funkcji y = -(x-2) +4 w przedziale (3, 5) jest A. 0 B. 5 C. 4 D. 3


Zadanie 13. (0—1) Ciąg arytmetyczny (a, ), określony dla n > 1, spełnia warunek a, +a, +a, =15. Wtedy A. a,=5 B. a,=6 C. a,=3 D. a,=4


Zadanie 14. (0—1) Dla pewnej liczby x ciąg (x, x + 4,16) jest geometryczny. Liczba x jest równa A. 8 B. 4 Cc 2 D. 0


Zadanie 15. (0—1) W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta a jest równa „3 . Zatem A. a=609 B. 2e(40,60) CC. ae(30,409) D. a=309

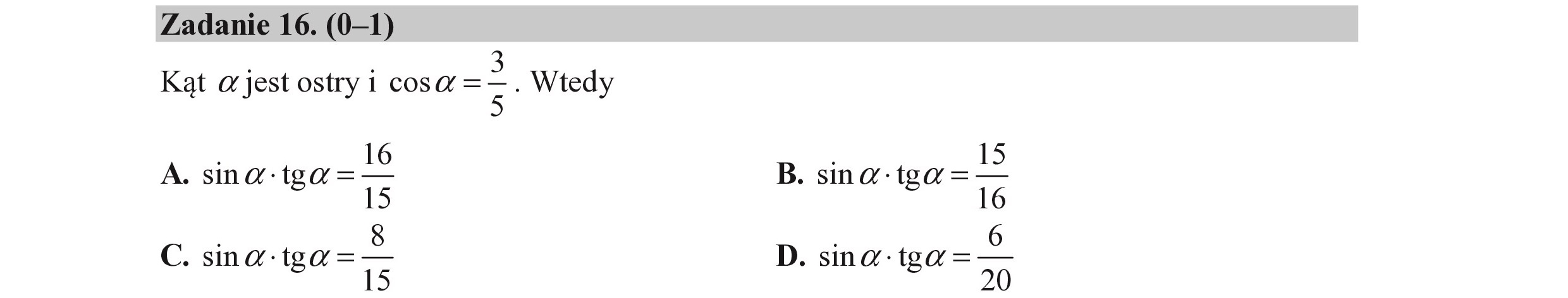
Zadanie 16. (0—1) Kąt a jest ostry i cosa = > „ Wtedy A. sina-1g0=-3 B. sina-1g0= > C. sna:tga =— D. śnardgir=""- JE 20


Zadanie 17. (0—1) Dany jest okrąg o środku 5. Punkty K, Z 1 M leżą na tym okręgu. Na łuku KZ tego okręgu są oparte kąty KSZ i KML (zobacz rysunek), których miary a i 8 spełniają warunek a+]B=114* . Wynika stąd, że A. B=19 B. 8=389 C. 8=57 D. 8=76


Zadanie 18. (0—1) Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 80”. Kąt rozwarty tego równoległoboku ma miarę A. 120? B. 1257 c. 130? D. 135?


Zadanie 19. (0—1) Pole trójkąta o bokach długości 4 oraz 9 i kącie między nimi o mierze 60” jest równe A. 18 B. 9 C. 18/3 D. 93


Zadanie 20. (0—1) Proste o równaniach y=(3m—4)x+2 oraz y=(12—m)x+3m są równoległe, gdy A. m=4 B. m=3 C. m=—4 D. m=—-3


Zadanie 21. (0—1) Punkt A=(—3,2) jest końcem odcinka 4B, a punkt M =(4,1) jest środkiem tego odcinka. Długość odcinka AB jest równa A. 245 B. 4/5 Cc. 542 D. 1042


Zadanie 22. (0—1) Jeżeli © oznacza miarę kąta między przekątną sześcianu a przekątną Ściany bocznej tego sześcianu (zobacz rysunek), to (NIZA A. sina= 46 B. sina= 2 3 2 C. sina= = D. sna= 8


Zadanie 23. (0-1) Przekrój osiowy walca jest kwadratem o przekątnej 10/2. Pole powierzchni bocznej tego walca jest równe A. 50m B. 100m c. 200m D. 250n


Zadanie 24. (0—1) Abiturient jednego z liceów zestawił w tabeli oceny ze swojego Świadectwa ukończenia szkoły. Ocena 6 5 4 3 2 Mediana przedstawionego zestawu danych jest równa A. 3 B. 3,5 C. 4 D. 4,5


Zadanie 25. (0—1) W grupie liczącej 29 uczniów (dziewcząt i chłopców) jest 15 chłopców. Z. tej grupy trzeba wylosować jedną osobę. Prawdopodobieństwo zdarzenia polegającego na tym, że zostanie wylosowana dziewczyna, jest równe = B. — a > D. > 15 14 29 29


Zadanie 26. (0-2) Rozwiąż nierówność x +óx-16<0.


Zadanie 27. (0—2) Rozwiąż równanie (2 + 27) (x — 16) = (b


Zadanie 28. (0—2) W równoległoboku ABCD punkt £ jest środkiem boku BC. Z wierzchołka D poprowadzono prostą przecinającą bok BC w punkcie E. Proste AB i DE przecinają się w punkcie / (zobacz rysunek). Wykaż, że punkt B jest środkiem odcinka AF. JE, >


Zadanie 29. (0—2) Wykaż, że jeżeli a i b są liczbami rzeczywistymi dodatnimi, to (a+ (23 z 24. a


Zadanie 30. (0—2) Dziewiąty wyraz ciągu arytmetycznego (a, ), określonego dla n>1, jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.


Zadanie 31. (0—2) Punkty A=(2,4), B=(0,0), C=(4,—2) są wierzchołkami trójkąta ABC. Punkt D jest środkiem boku AC tego trójkąta. Wyznacz równanie prostej BD.


Zadanie 32. (0—5) W ostrosłupie prawidłowym trójkątnym ABCS krawędź podstawy ma długość a. Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy. (6 |


Zadanie 33. (0—4) Ze zbioru A=[-3,—2,—1,1,2,3| losujemy liczbę a, natomiast ze zbioru B= -1,0, 1, 2) losujemy liczbę b. Te liczby są — odpowiednio — współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej f (x) =ax+b. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja / jest rosnąca i ma dodatnie miejsce zerowe.


Zadanie 34. (0—4) W trójkącie prostokątnym ACB przyprostokątna AC ma długość 5, a promień okręgu wpisanego w ten trójkąt jest równy 2. Oblicz pole trójkąta ACB.






























