MATEMATYKA 2018 CZERWIEC MATURA PODSTAWOWA
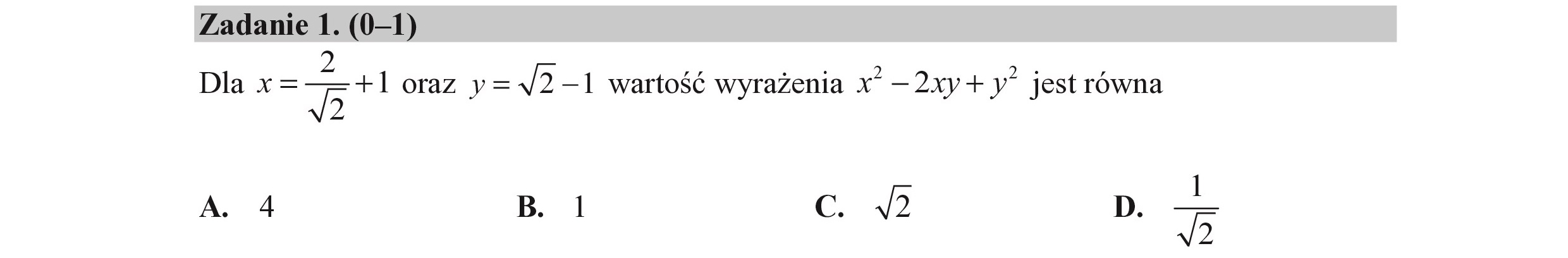
Zadanie 1. (0—1) 2 , . Dla x= NZ) +] oraz y= N2-1 wartość wyrażenia x —2xy+y” jest równa A. 4 B. 1 Ć 43 D. — N2

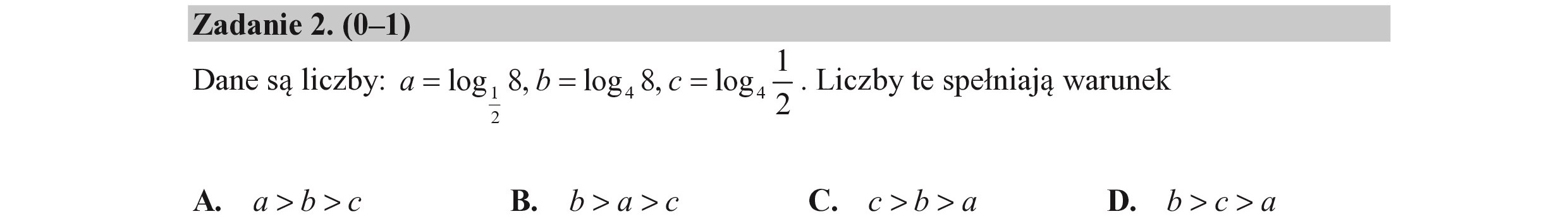
Zadanie 2. (0—1) Dane są liczby: a = log, 8,b=log,8,c=log 3: Liczby te spełniają warunek 2 A. a>b>c B. b>a>c C. c>b>a D. b>c>a

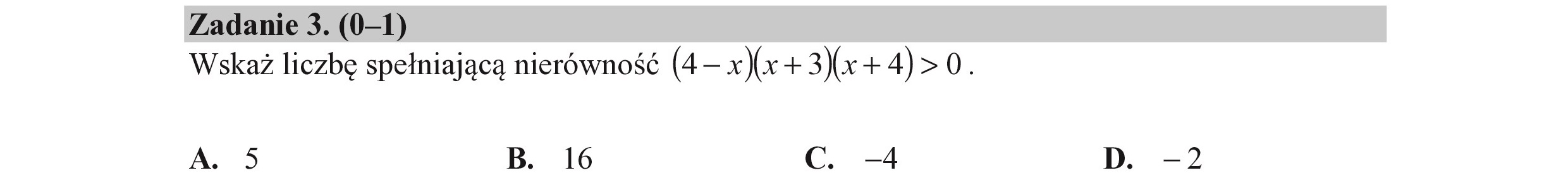
Zadanie 3. (0—1) Wskaż liczbę spełniającą nierówność (4— x)(x + 3)(x + 4)> 0. A. 5 B. I6 Cc. 4


Zadanie 4. (0—1) Po dwukrotnej obniżce, za każdym razem o 10% w stosunku do ceny obowiązującej w chwili obniżki, komputer kosztuje 1944 złote. Stąd wynika, że przed tymi obniżkami ten komputer kosztował A. 2200 złotych. B. 2300 złotych. C. 2400 złotych. D. 3000 złotych.


Zadanie 5. (0—1) Na rysunku przedstawiony jest przedział (-10,k), gdzie k jest liczbą całkowitą. Suma wszystkich liczb całkowitych należących do tego przedziału jest równa 21. SKANIE WENA GA -10 k x Stąd wynika, że A. k=9 B. k=1l C. k=2l D. k=3I


Zadanie 6. (0—1) Równanie x — = 2x+1 A. ma dokładnie dwa rozwiązania rzeczywiste. B. ma dokładnie trzy rozwiązania rzeczywiste. C. ma dokładnie jedno rozwiązanie rzeczywiste. D. nie ma rozwiązań.


Zadanie 7. (0—1) Liczbę r można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Dwudziestą cyfrą po przecinku jego rozwinięcia jest A. 2 B. 0 G 1 D. 6


Zadanie 8. (0—1) 20_5,420 Liczba 280,40 jest równa A. 0 B. 27-92 C. 7 D. 4-27


Zadanie 9. (0—1) Funkcja / jest określona wzorem f/(x)=—2(x+ 2)! (x-3) dla każdej liczby rzeczywistej x%—2. Wartość funkcji / dla argumentu 2 jest równa A. —8 B. — Cc. u 2 Ź


Zadanie 10. (0—1) Największą wartością funkcji y = —(x -2) +4 w przedziale (3, 5) jest A. 4 B. 3 c. 0 D. 5


Zadanie 11. (0—1) Funkcja liniowa /(x)= (1 — m x +m — 1 nie ma miejsc zerowych dla A. m=l B m=0 C. m=—l m=—2

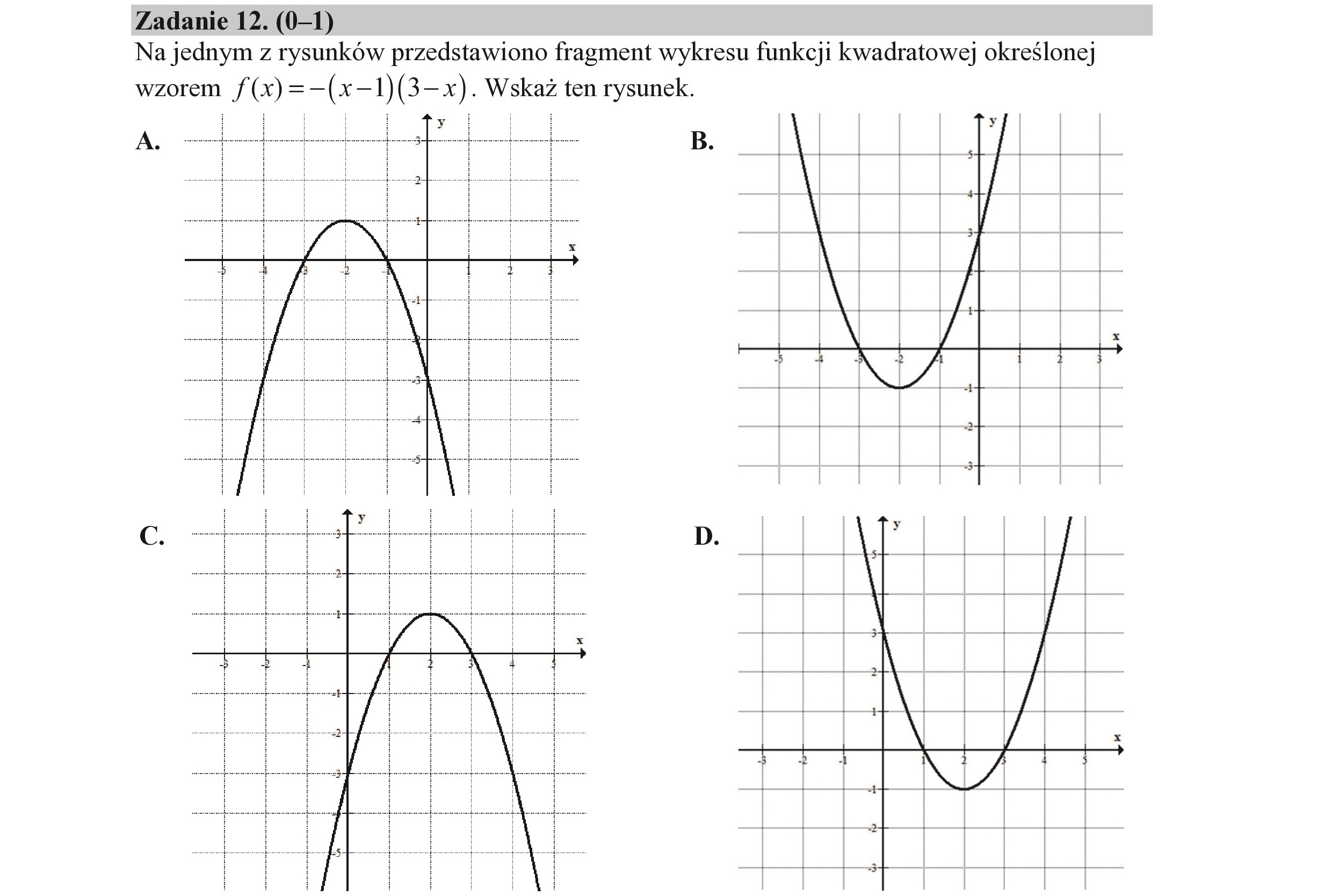
Zadanie 12. (0—1) Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem f(x) =-(x-1)(3—x). Wskaż ten rysunek. y | A.


Zadanie 13. (0—1) Wszystkie wyrazy ciągu geometrycznego (a, ) określonego dla n > 1 są dodatnie i 3a =2a;. Stąd wynika, że iloraz q tego ciągu jest równy


Zadanie 14. (0—1) Dany jest ciąg arytmetyczny (a,) określony wzorem a, =16-1-n dla każdej liczby całkowitej n > 1. Różnica 7 tego ciągu jest równa C. r=—L D. r=151 A. r=—1I6 B. r=— 7


Zadanie 15. (0—1) Liczba 1—tg40” jest A. ujemna. B. dodatnia, ale mniejsza od 0,1. C. większa od 0,1, ale mniejsza od 0,5. D. większa od 0,5.

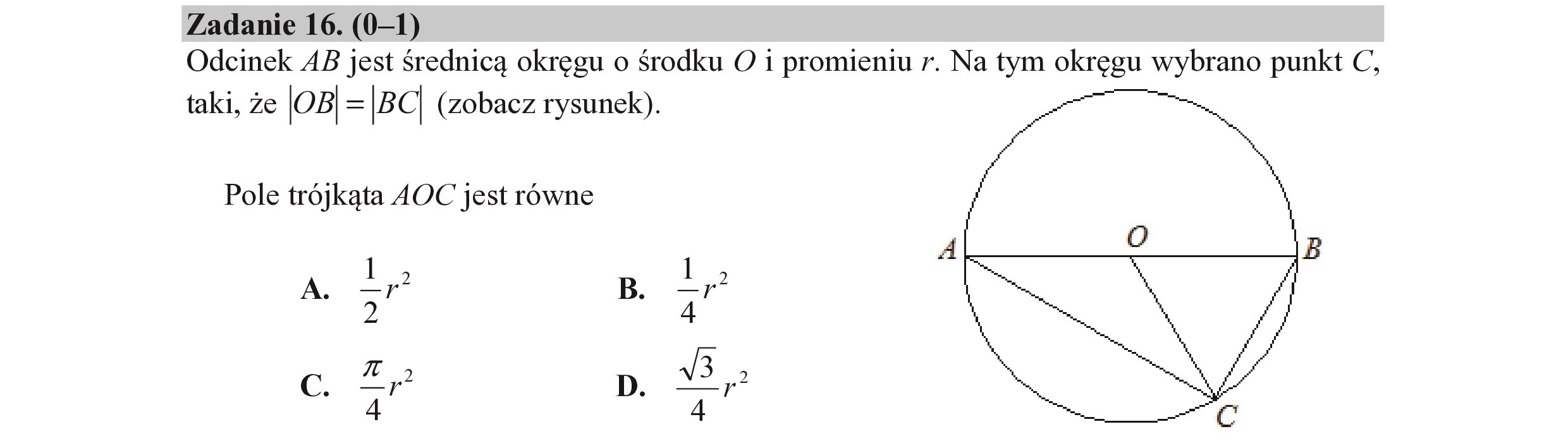
Zadanie 16. (0—1) Odcinek 4B jest średnicą okręgu o środku O i promieniu 7. Na tym okręgu wybrano punkt C, taki, że |OB| = |3C (zobacz rysunek). Pole trójkąta AOC jest równe A B A 1,2 B 1 4 [© 2,2 D. AB,» - - ' =


Zadanie 17. (0—1) Okrąg o środku S, = (2, 1) i promieniu r oraz okrąg o środku ŚS,= (5, 5) i promieniu 4 są styczne zewnętrznie. Wtedy A. r=l B. r=2 C. F=8 D. r=4


Zadanie 18. (0—1) Długości boków trapezu równoramiennego są równe 12, 13, 2, 13. Wysokość h tego trapezu jest równa A. 5 B. 8 c. 10 12


Zadanie 19. (0—1) Miary kątów pewnego czworokąta pozostają w stosunku 2:3:3:4. Wynika stąd, że najmniejszy kąt tego czworokąta ma miarę A. 60? B. 509 c. 40? D. 307


Zadanie 20. (0—1) Dany jest walec, w którym wysokość jest równa promieniowi podstawy. Objętość tego walca jest równa 277 . Wynika stąd, że promień podstawy tego walca jest równy A. 9 B. 6 Cc. 3 D. 2


Zadanie 21. (0—1) Stożek o promieniu podstawy r i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy A. Ę B. 12 c. AT D. 4

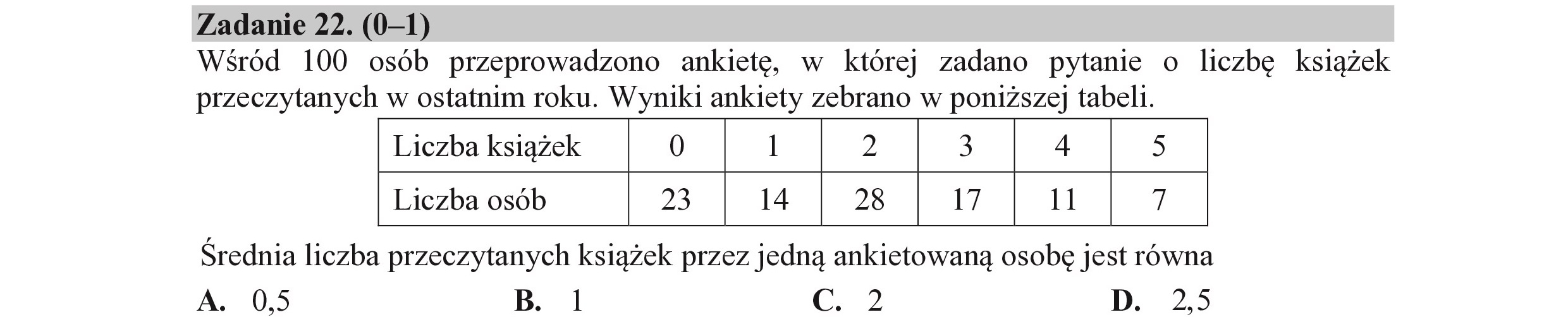
Zadanie 22. (0—1) Wśród 100 osób przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli. Liczba książek 0 I 2 3 - 5 Liczba osób 23 14 28 17 11 7 Średnia liczba przeczytanych książek przez jedną ankietowaną osobę jest równa A. 0,5 B. I c. 2 D. 25


Zadanie 23. (0—1) Gdy dodamy liczbę wszystkich krawędzi pewnego graniastosłupa do liczby wszystkich jego wierzchołków, to otrzymamy w wyniku 15. Liczba wszystkich krawędzi tego graniastosłupa jest równa A. 9 B. 7 Cc. 6 D. 5


Zadanie 24. (0—1) Liczba wszystkich dodatnich liczb czterocyfrowych parzystych, w których zapisie nie występują cyfry 0 1 2, jest równa A. 8:8:8-3 B. 8-7:6:3 C. 8-10-10-4 D. 9-8-7-4


Zadanie 25. (0—1) W pudełku znajdują się dwie kule: czarna i biała. Czterokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie trzy razy w czterech losowaniach wyciągniemy kulę koloru białego, jest równe A. — B. > C. 8 a|w u 4


Zadanie 26. (0-2) Rozwiąż nierówność 2x(1-x)+l-x<0.


Zadanie 27. (0-2) Wykresem funkcji kwadratowej f określonej wzorem f (aej=uć" +bx+c jest parabola, na której leży punkt A = (0,—5). Osią symetrii tej paraboli jest prosta o równaniu x=7. Oblicz wartości współczynników bic.


Zadanie 28. (0—2) Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych liczb naturalnych przez 8 jest równa 6.

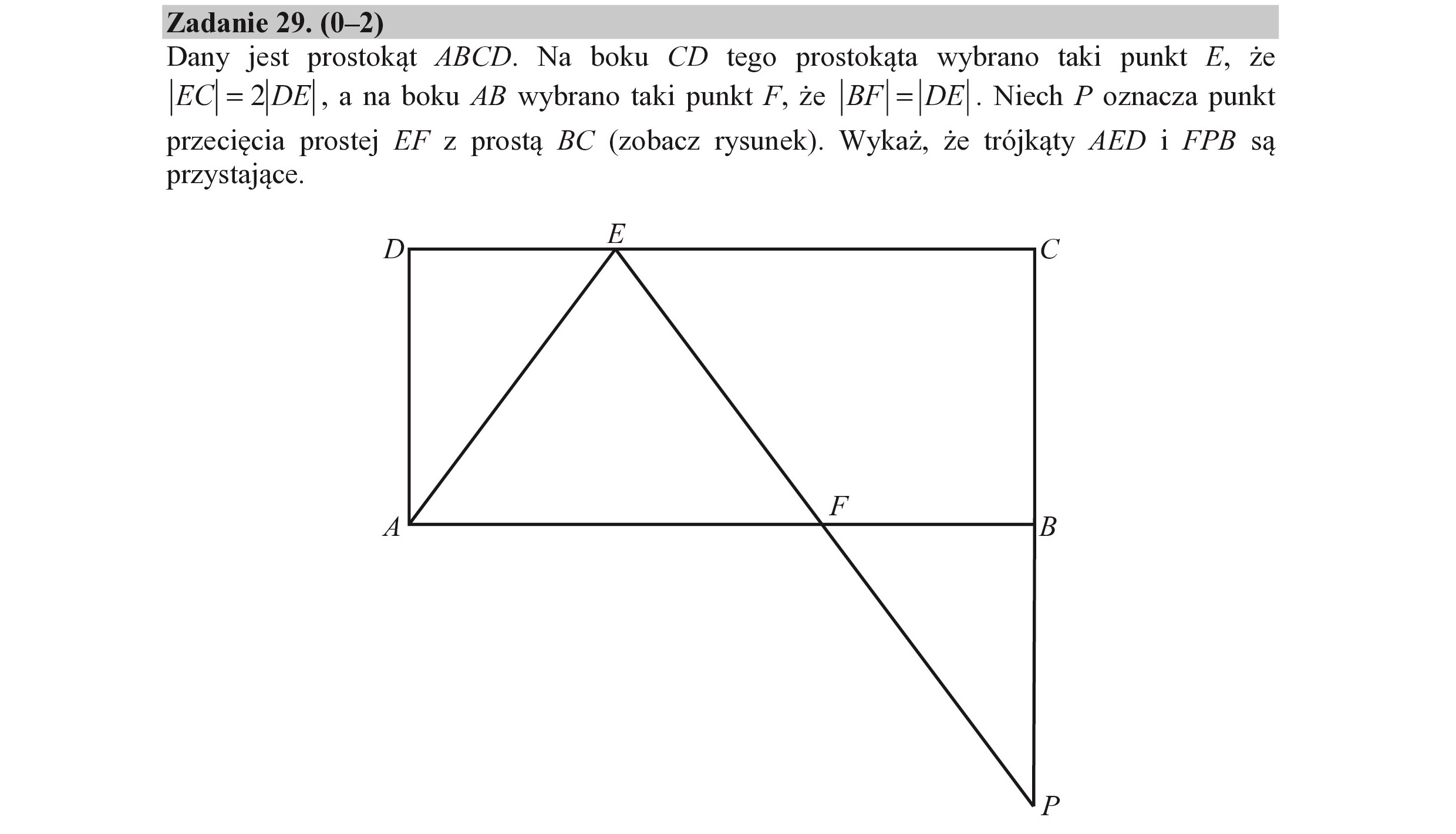
Zadanie 29. (0—2) Dany jest prostokąt ABCD. Na boku CD tego prostokąta wybrano taki punkt E£, że |zC = 2|DE , a na boku AB wybrano taki punkt 7, że |BF | =|DE|. Niech P oznacza punkt przecięcia prostej EF z prostą BC (zobacz rysunek). Wykaż, że trójkąty AED i FPB są przystające. B


Zadanie 30. (0—2) Kąta jest ostry i sna +cosa= 2. Oblicz wartość wyrażenia tg« +——. tga


Zadanie 31. (0—2) Rzucamy cztery razy symetryczną monetą. Po przeprowadzonym doświadczeniu zapisujemy liczbę uzyskanych orłów (od 0 do 4) i liczbę uzyskanych reszek (również od 0 do 4). Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych czterech rzutach liczba uzyskanych orłów będzie większa niż liczba uzyskanych reszek.


Zadanie 32. (0—5) Dany jest ostrosłup prawidłowy czworokątny o wysokości H =16. Cosinus kąta nachylenia 3 krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy —. Oblicz pole powierzchni bocznej tego ostrosłupa.


Zadanie 33. (0—4) W ciągu arytmetycznym (a,), określonym dla liczb naturalnych n 2 1, wyraz szósty jest liczbą dwa razy większą od wyrazu piątego, a suma dziesięciu początkowych wyrazów tego "=" : 15 : . s. . ciągu jest równa 5,, =—. Oblicz wyraz pierwszy oraz różnicę tego ciągu. gu J U Wy


Zadanie 34. (0—4) Punkty A=(—1L1) i C=(1,9) są wierzchołkami trójkąta równoramiennego ABC, w którym |AC |= |BC |. Podstawa AB tego trójkąta zawiera się w prostej o równaniu y= 1x+ż 3. Oblicz współrzędne wierzchołka B tego trójkąta.

MATEMATYKA 2018 CZERWIEC MATURA PODSTAWOWA
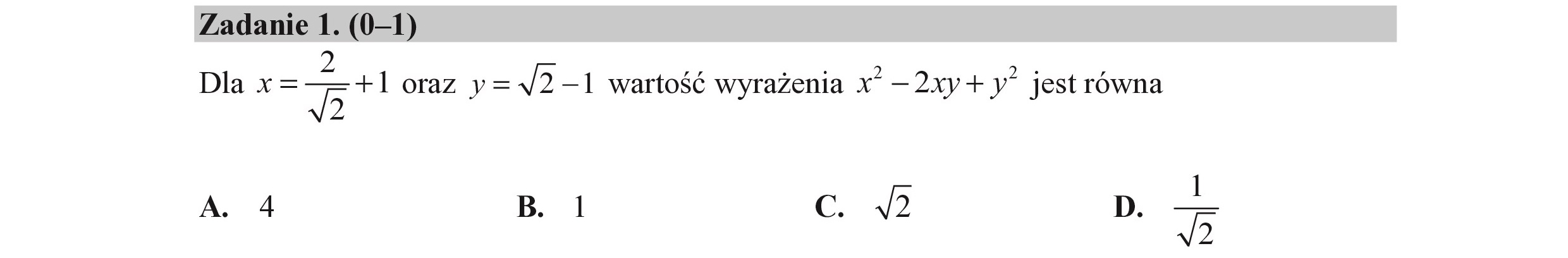
Zadanie 1. (0—1) 2 , . Dla x= NZ) +] oraz y= N2-1 wartość wyrażenia x —2xy+y” jest równa A. 4 B. 1 Ć 43 D. — N2

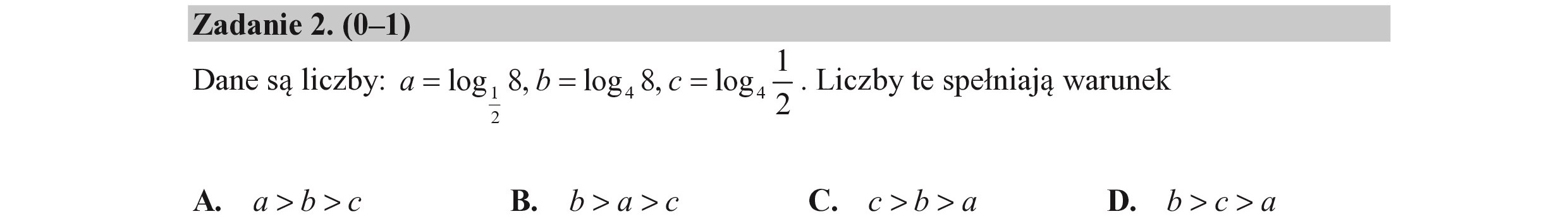
Zadanie 2. (0—1) Dane są liczby: a = log, 8,b=log,8,c=log 3: Liczby te spełniają warunek 2 A. a>b>c B. b>a>c C. c>b>a D. b>c>a

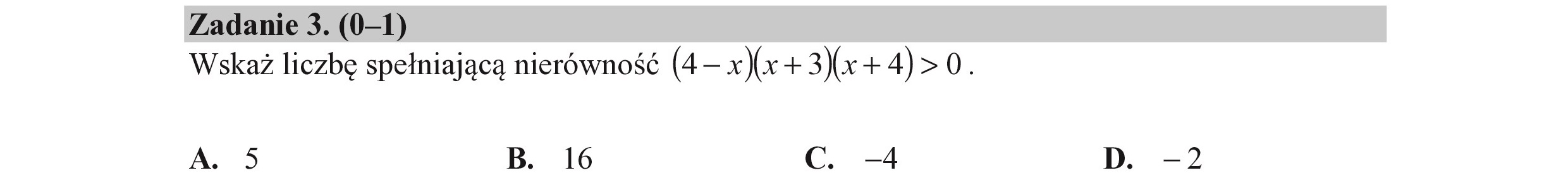
Zadanie 3. (0—1) Wskaż liczbę spełniającą nierówność (4— x)(x + 3)(x + 4)> 0. A. 5 B. I6 Cc. 4


Zadanie 4. (0—1) Po dwukrotnej obniżce, za każdym razem o 10% w stosunku do ceny obowiązującej w chwili obniżki, komputer kosztuje 1944 złote. Stąd wynika, że przed tymi obniżkami ten komputer kosztował A. 2200 złotych. B. 2300 złotych. C. 2400 złotych. D. 3000 złotych.


Zadanie 5. (0—1) Na rysunku przedstawiony jest przedział (-10,k), gdzie k jest liczbą całkowitą. Suma wszystkich liczb całkowitych należących do tego przedziału jest równa 21. SKANIE WENA GA -10 k x Stąd wynika, że A. k=9 B. k=1l C. k=2l D. k=3I


Zadanie 6. (0—1) Równanie x — = 2x+1 A. ma dokładnie dwa rozwiązania rzeczywiste. B. ma dokładnie trzy rozwiązania rzeczywiste. C. ma dokładnie jedno rozwiązanie rzeczywiste. D. nie ma rozwiązań.


Zadanie 7. (0—1) Liczbę r można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Dwudziestą cyfrą po przecinku jego rozwinięcia jest A. 2 B. 0 G 1 D. 6


Zadanie 8. (0—1) 20_5,420 Liczba 280,40 jest równa A. 0 B. 27-92 C. 7 D. 4-27


Zadanie 9. (0—1) Funkcja / jest określona wzorem f/(x)=—2(x+ 2)! (x-3) dla każdej liczby rzeczywistej x%—2. Wartość funkcji / dla argumentu 2 jest równa A. —8 B. — Cc. u 2 Ź


Zadanie 10. (0—1) Największą wartością funkcji y = —(x -2) +4 w przedziale (3, 5) jest A. 4 B. 3 c. 0 D. 5


Zadanie 11. (0—1) Funkcja liniowa /(x)= (1 — m x +m — 1 nie ma miejsc zerowych dla A. m=l B m=0 C. m=—l m=—2


Zadanie 12. (0—1) Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem f(x) =-(x-1)(3—x). Wskaż ten rysunek. y | A.


Zadanie 13. (0—1) Wszystkie wyrazy ciągu geometrycznego (a, ) określonego dla n > 1 są dodatnie i 3a =2a;. Stąd wynika, że iloraz q tego ciągu jest równy


Zadanie 14. (0—1) Dany jest ciąg arytmetyczny (a,) określony wzorem a, =16-1-n dla każdej liczby całkowitej n > 1. Różnica 7 tego ciągu jest równa C. r=—L D. r=151 A. r=—1I6 B. r=— 7


Zadanie 15. (0—1) Liczba 1—tg40” jest A. ujemna. B. dodatnia, ale mniejsza od 0,1. C. większa od 0,1, ale mniejsza od 0,5. D. większa od 0,5.


Zadanie 16. (0—1) Odcinek 4B jest średnicą okręgu o środku O i promieniu 7. Na tym okręgu wybrano punkt C, taki, że |OB| = |3C (zobacz rysunek). Pole trójkąta AOC jest równe A B A 1,2 B 1 4 [© 2,2 D. AB,» - - ' =


Zadanie 17. (0—1) Okrąg o środku S, = (2, 1) i promieniu r oraz okrąg o środku ŚS,= (5, 5) i promieniu 4 są styczne zewnętrznie. Wtedy A. r=l B. r=2 C. F=8 D. r=4


Zadanie 18. (0—1) Długości boków trapezu równoramiennego są równe 12, 13, 2, 13. Wysokość h tego trapezu jest równa A. 5 B. 8 c. 10 12


Zadanie 19. (0—1) Miary kątów pewnego czworokąta pozostają w stosunku 2:3:3:4. Wynika stąd, że najmniejszy kąt tego czworokąta ma miarę A. 60? B. 509 c. 40? D. 307


Zadanie 20. (0—1) Dany jest walec, w którym wysokość jest równa promieniowi podstawy. Objętość tego walca jest równa 277 . Wynika stąd, że promień podstawy tego walca jest równy A. 9 B. 6 Cc. 3 D. 2


Zadanie 21. (0—1) Stożek o promieniu podstawy r i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy A. Ę B. 12 c. AT D. 4


Zadanie 22. (0—1) Wśród 100 osób przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli. Liczba książek 0 I 2 3 - 5 Liczba osób 23 14 28 17 11 7 Średnia liczba przeczytanych książek przez jedną ankietowaną osobę jest równa A. 0,5 B. I c. 2 D. 25


Zadanie 23. (0—1) Gdy dodamy liczbę wszystkich krawędzi pewnego graniastosłupa do liczby wszystkich jego wierzchołków, to otrzymamy w wyniku 15. Liczba wszystkich krawędzi tego graniastosłupa jest równa A. 9 B. 7 Cc. 6 D. 5


Zadanie 24. (0—1) Liczba wszystkich dodatnich liczb czterocyfrowych parzystych, w których zapisie nie występują cyfry 0 1 2, jest równa A. 8:8:8-3 B. 8-7:6:3 C. 8-10-10-4 D. 9-8-7-4


Zadanie 25. (0—1) W pudełku znajdują się dwie kule: czarna i biała. Czterokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie trzy razy w czterech losowaniach wyciągniemy kulę koloru białego, jest równe A. — B. > C. 8 a|w u 4


Zadanie 26. (0-2) Rozwiąż nierówność 2x(1-x)+l-x<0.


Zadanie 27. (0-2) Wykresem funkcji kwadratowej f określonej wzorem f (aej=uć" +bx+c jest parabola, na której leży punkt A = (0,—5). Osią symetrii tej paraboli jest prosta o równaniu x=7. Oblicz wartości współczynników bic.


Zadanie 28. (0—2) Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych liczb naturalnych przez 8 jest równa 6.


Zadanie 29. (0—2) Dany jest prostokąt ABCD. Na boku CD tego prostokąta wybrano taki punkt E£, że |zC = 2|DE , a na boku AB wybrano taki punkt 7, że |BF | =|DE|. Niech P oznacza punkt przecięcia prostej EF z prostą BC (zobacz rysunek). Wykaż, że trójkąty AED i FPB są przystające. B


Zadanie 30. (0—2) Kąta jest ostry i sna +cosa= 2. Oblicz wartość wyrażenia tg« +——. tga


Zadanie 31. (0—2) Rzucamy cztery razy symetryczną monetą. Po przeprowadzonym doświadczeniu zapisujemy liczbę uzyskanych orłów (od 0 do 4) i liczbę uzyskanych reszek (również od 0 do 4). Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych czterech rzutach liczba uzyskanych orłów będzie większa niż liczba uzyskanych reszek.


Zadanie 32. (0—5) Dany jest ostrosłup prawidłowy czworokątny o wysokości H =16. Cosinus kąta nachylenia 3 krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy —. Oblicz pole powierzchni bocznej tego ostrosłupa.


Zadanie 33. (0—4) W ciągu arytmetycznym (a,), określonym dla liczb naturalnych n 2 1, wyraz szósty jest liczbą dwa razy większą od wyrazu piątego, a suma dziesięciu początkowych wyrazów tego "=" : 15 : . s. . ciągu jest równa 5,, =—. Oblicz wyraz pierwszy oraz różnicę tego ciągu. gu J U Wy


Zadanie 34. (0—4) Punkty A=(—1L1) i C=(1,9) są wierzchołkami trójkąta równoramiennego ABC, w którym |AC |= |BC |. Podstawa AB tego trójkąta zawiera się w prostej o równaniu y= 1x+ż 3. Oblicz współrzędne wierzchołka B tego trójkąta.






























