MATEMATYKA 2017 CZERWIEC MATURA PODSTAWOWA

Zadanie 1. (0—1) Liczba jo — 2) -|4— 7) jest równa A. 4 B. 10 —1y


Zadanie 2. (0—1) Iloczyn dodatnich liczb a i b jest równy 1350. Ponadto 15% liczby a jest równe 10% liczby b. Stąd wynika, że b jest równe A.9 B. 18 C. 45 D. 50


Zadanie 3. (0—1) Suma 16** +16*' +16” +16" jest równa A. 4 B. 4* c. 4* D. 4?


Zadanie 4. (0—1) Liczba log, 27 — log, 1 jest równa A. 0 B. I

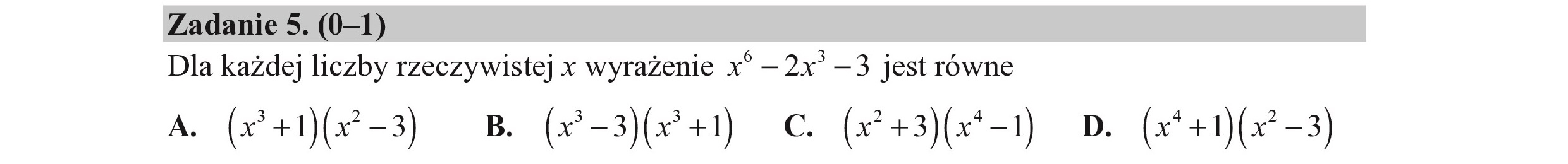
Zadanie 5. (0—1) Dla każdej liczby rzeczywistej x wyrażenie x” — 2x* —3 jest równe A. (x +1)fó-3) (B. (»-3)(e+1) C. (x +3)fd-1) D. (*+1)(x*-3)

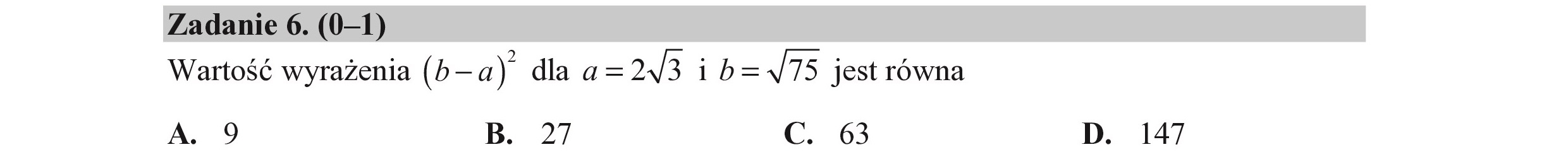
Zadanie 6. (0—1) Wartość wyrażenia (b— a) dla a=243 i b=

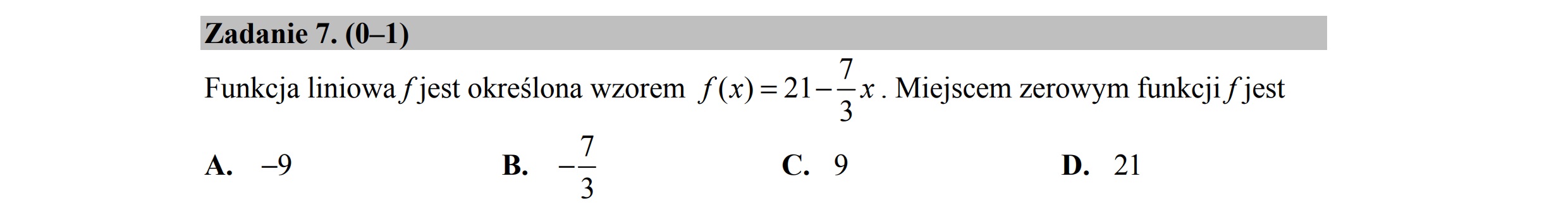
Zadanie 7. (0—1) Funkcja liniowa f jest określona wzorem f(x) =21— zx . Miejscem zerowym funkcji / jest A. 9 B. -3 c 9 D. 21


Zadanie 8. (0—1)
. xty=l RE 2. . .
Rozwiązaniem układu równań | * z niewiadomymi x i y jest para liczb dodatnich.
X-p=
Wynika stąd, że
A. b<-l B. b=—l C. -1

Zadanie 9. (0—1) Funkcja kwadratowa f jest określona wzorem f(x)=x'+bx+c oraz f(-1)=/f(3)=1. Współczynnik b jest równy A. 2 B. —I c. 0 D. 3

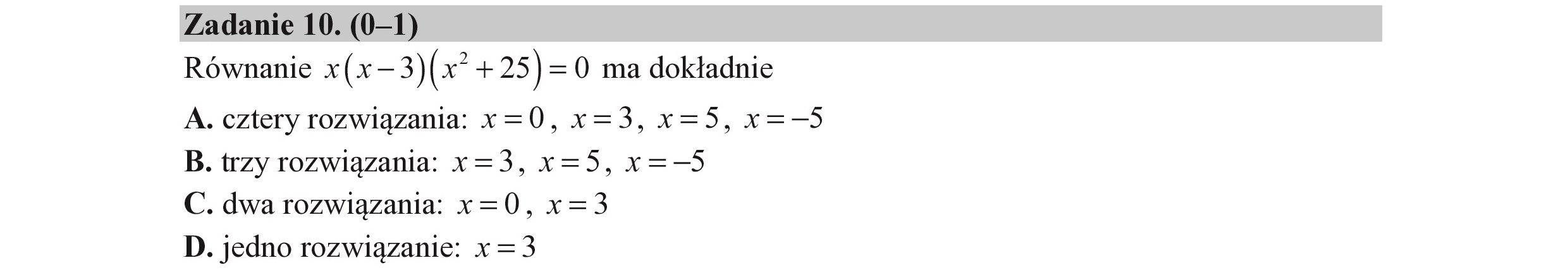
Zadanie 10. ra 1) Równanie x(x-3 )(e +25)=0 dokładnie A. cztery rozwiązania: x=0, x=3, x=5, x=—5 B. trzy rozwiązania: x=3, x=5, x= 5 -5, C. dwa rozwiązania: x=0, x=3 D. jedno rozwiązanie: x = s


Zadanie 11. (0—1) Funkcja kwadratowa f jest określona wzorem f(x) =(x-3)(7-x). Wierzchołek paraboli będącej wykresem funkcji fnależy do prostej o równaniu A. y=-5 B. y=5 C. y=-—4 D. y=4


Zadanie 12. (0—1) Punkt 4=(2017,0) należy do wykresu funkcji f określonej wzorem A. f(x)=(x+2017) B. f(x)=x —2017 C. f(x)=(x+2017)(x-—2017) D. /(x)=x +2017


Zadanie 13. (0—1) W ciągu arytmetycznym (a,), określonym dla n>l, spełniony jest warunek 2a, =a, +a, +1. Różnica r tego ciągu jest równa A. 0 B. Ka: W |< . 3

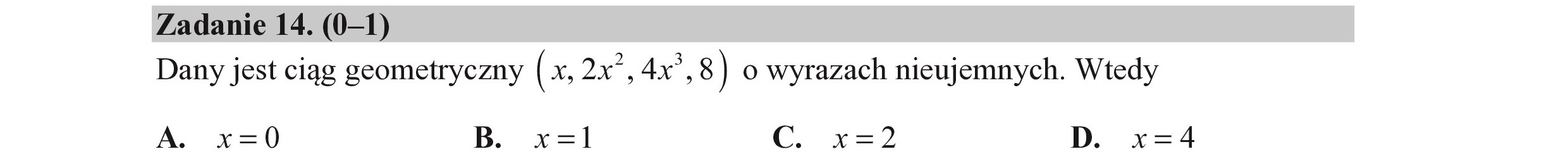
Zadanie 14. (0-1) Dany jest ciąg geometryczny (x. 2% ,4X , 8) o wyrazach nieujemnych. Wtedy A. x=0 B. x=l1 CC. x=2 D. x=4


Zadanie 15. (0—1) . ! 12 ; " , Kąt a jest ostry 1 tga = g” Wówczas sina jest równy 3 B 12 5 A. — : c. — 17 17 13 I2 13

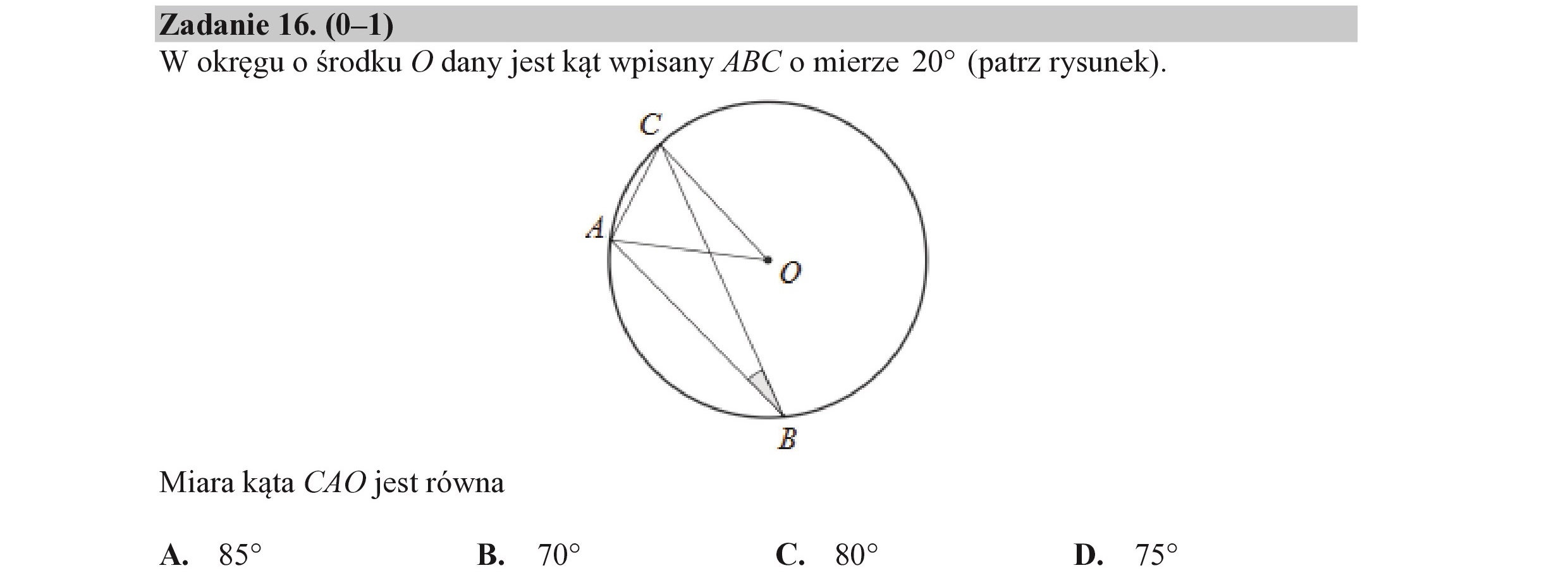
Zadanie 16. (0—1) W okręgu o środku O dany jest kąt wpisany ABC o mierze 20? (patrz rysunek). Miara kąta CAO jest równa A. 859 B. 707 c. 80? D. 757


Zadanie 17. (0—1)
Odcinek BD jest zawarty w dwusiecznej kąta ostrego ABC trójkąta prostokątnego, w którym
przyprostokątne AC 1 BC mają długości odpowiednio 5 13.
B
D
3
a A
C D 5
Wówczas miara g kąta DBC spełnia warunek
A. 20
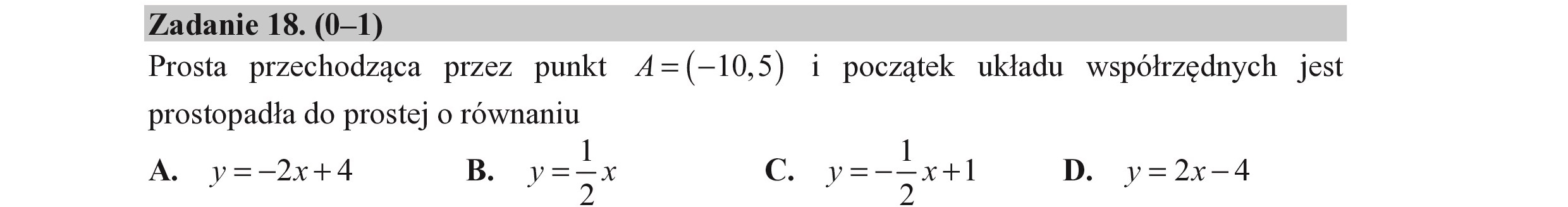
Zadanie 18. (0—1) Prosta przechodząca przez punkt A=(-10,5) i początek układu współrzędnych jest prostopadła do prostej o równaniu A. y=-2x+4 B. y=żx c. p=-zak1 D. v=2x-4


Zadanie 19. (0—1) Punkty A=(-21,11) i B=(3,17) są końcami odcinka AB. Obrazem tego odcinka w symetrii względem osi Ox układu współrzędnych jest odcinek AB”. Środkiem odcinka 4'B' jest punkt o współrzędnych A. (-9,—14) B. (-9,14) c. (9,—14) D. (9,14)


Zadanie 20. (0—1) . . Pp? AA . 5 (Es14 Trójkąt ABC jest podobny do trójkąta ABC wskali > , przy czym |4B| = G AB|. Stosunek pola trójkąta ABC do pola trójkąta 4 BC” jest równy A. — B. JE p. > 23 5 2 4


Zadanie 21. (0—1) Pole koła opisanego na trójkącie równobocznym jest równe z . Długość boku tego trójkąta jest równa A. A B. z c. Ju D. 3a

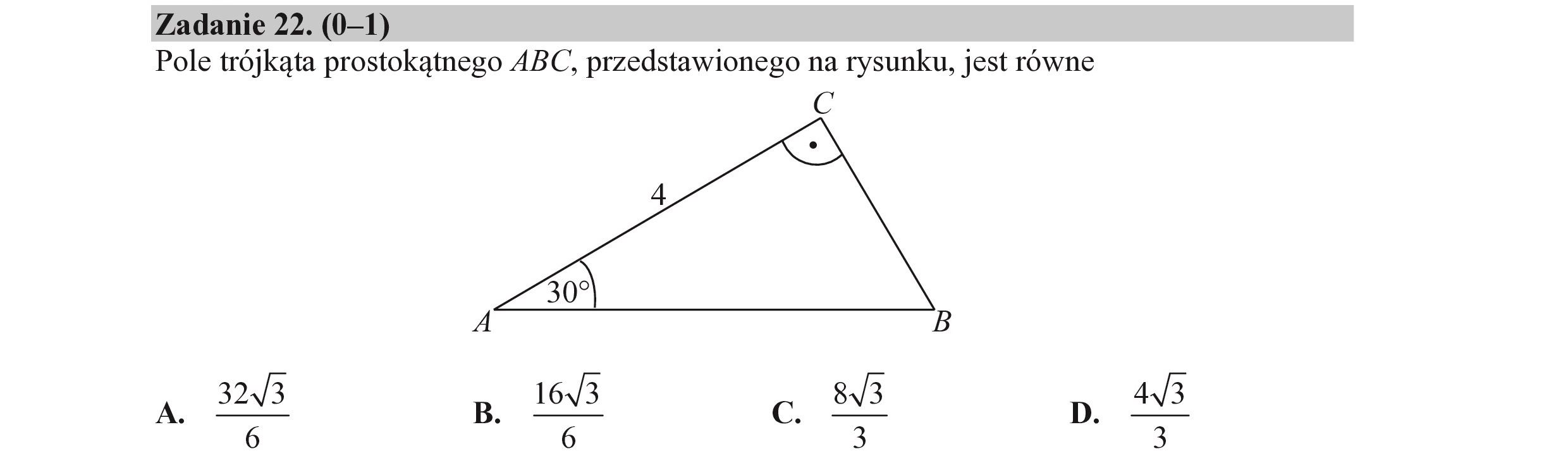
Zadanie 22. (0—1) Pole trójkąta prostokątnego ABC, przedstawionego na rysunku, jest równe (e


Zadanie 23. (0—1) Długość przekątnej sześcianu jest równa 6 . Stąd wynika, że pole powierzchni całkowitej tego sześcianu jest równe A. 72 B. 48 c. 152 D. 108


Zadanie 24. (0—1) Pole powierzchni bocznej walca jest równe lóx, a promień jego podstawy ma długość 2. Wysokość tego walca jest równa A. 4 B. 8 C. 4n D. 8n


Zadanie 25. (0—1) Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania pary liczb, których iloczyn jest większy od 20, jest równe A. — B. — c. 2 p. > 6 36 A 8

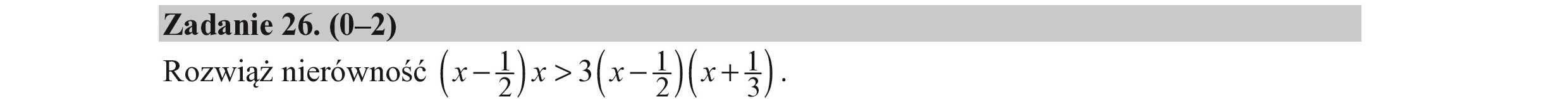
Zadanie 26. (0—2) Rozwiąż nierówność (x- ) 1) x > 3(x- p 1) (x de 1).

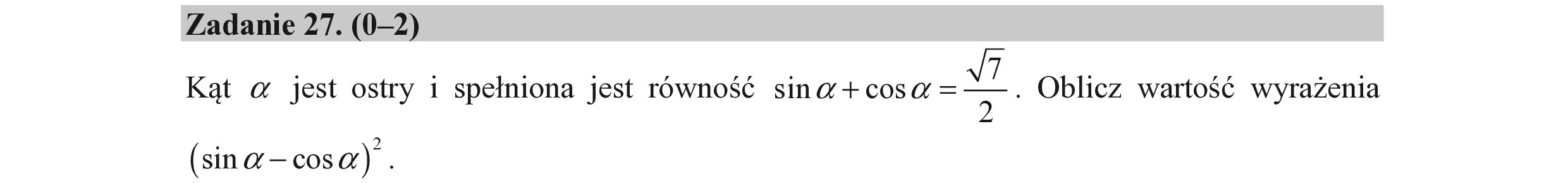
Zadanie 27. (0—2) Kąt a jest ostry i spełniona jest równość sina + DARERE Ty + Oblicz wartość wyrażenia (sin 2 — cos a) .


Zadanie 28. (0—2) Dwusieczna kąta ostrego ABC przecina przyprostokątną AC trójkąta prostokątnego ABC w punkcie D. B Udowodnij, że jeżeli |4D|=|BD „to [EP|->-|BD|.


Zadanie 29. (0-2) Wykaż, że prawdziwa jest nierówność y 2 p J (1,5) < 62 i


Zadanie 30. (0—2) Suma trzydziestu początkowych wyrazów ciągu arytmetycznego (a, ) , określonego dla n> l, jest równa 30. Ponadto a., = 30. Oblicz różnicę tego ciągu.


Zadanie 31. (0—2) Ze zbioru liczb 11, 2, 3, 4, 5, 6, 7,8,9,10,11, 12, 13, 14, 15) losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę (a, b), gdzie a jest wynikiem pierwszego losowania, b jest wynikiem drugiego losowania. Oblicz, ile jest wszystkich par (a, b) takich, że iloczyn a:b jest liczbą parzystą.


Zadanie 32. (0—4) Ramię trapezu równoramiennego ABCD ma długość 426. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2: 3. Oblicz pole tego trapezu.


Zadanie 33. (0—4) Punkty A=(-2,—8) i B=(14,—8) są wierzchołkami trójkąta równoramiennego ABC, w którym |4B8|=|AC|. Wysokość AD tego trójkąta jest zawarta w prostej o równaniu l . . . y= zg 7. Oblicz współrzędne wierzchołka C tego trójkąta.

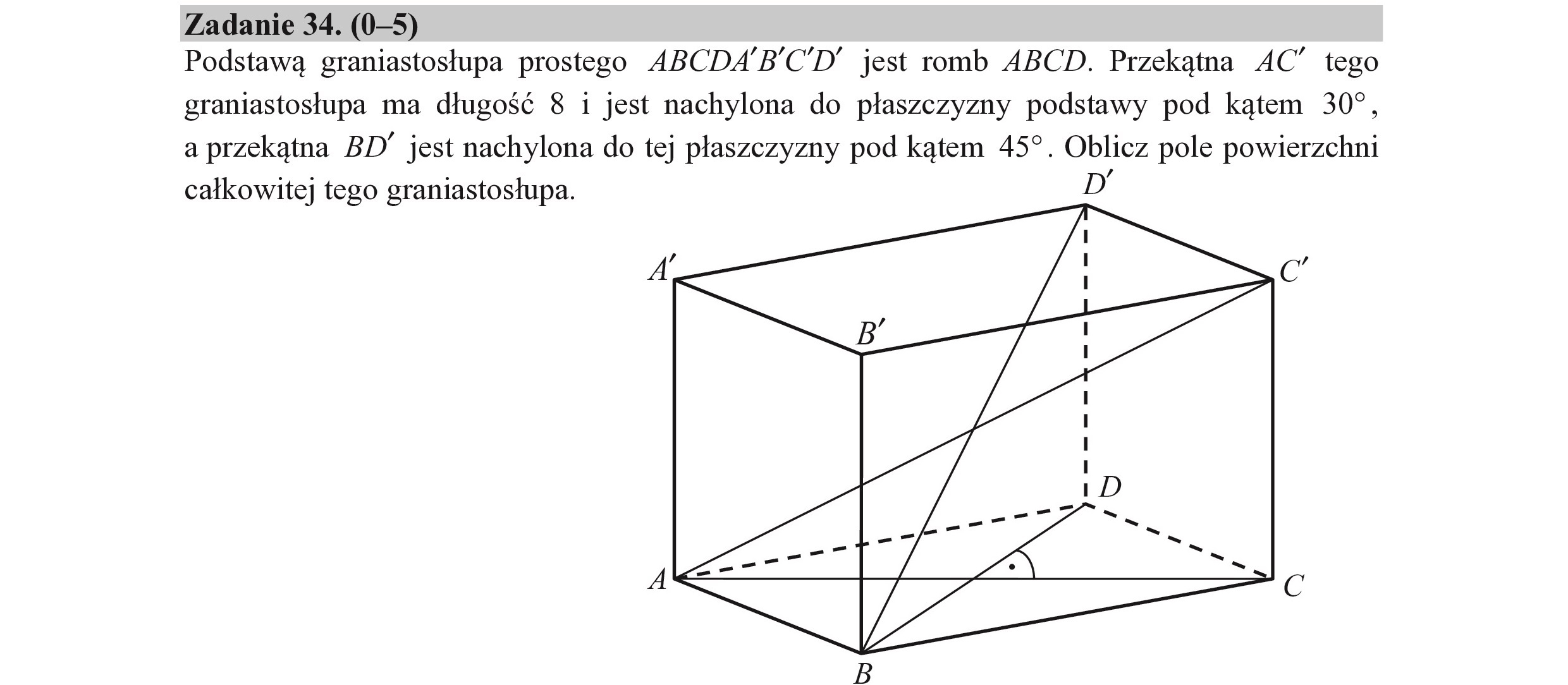
Zadanie 34. (0—5) Podstawą graniastosłupa prostego ABCDA BCD” jest romb ABCD. Przekątna AC tego graniastosłupa ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem 307, a przekątna BD” jest nachylona do tej płaszczyzny pod kątem 45”. Oblicz pole powierzchni całkowitej tego graniastosłupa. D

MATEMATYKA 2017 CZERWIEC MATURA PODSTAWOWA

Zadanie 1. (0—1) Liczba jo — 2) -|4— 7) jest równa A. 4 B. 10 —1y


Zadanie 2. (0—1) Iloczyn dodatnich liczb a i b jest równy 1350. Ponadto 15% liczby a jest równe 10% liczby b. Stąd wynika, że b jest równe A.9 B. 18 C. 45 D. 50


Zadanie 3. (0—1) Suma 16** +16*' +16” +16" jest równa A. 4 B. 4* c. 4* D. 4?


Zadanie 4. (0—1) Liczba log, 27 — log, 1 jest równa A. 0 B. I

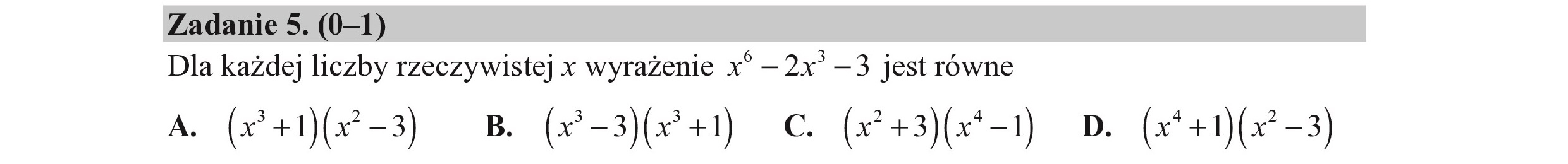
Zadanie 5. (0—1) Dla każdej liczby rzeczywistej x wyrażenie x” — 2x* —3 jest równe A. (x +1)fó-3) (B. (»-3)(e+1) C. (x +3)fd-1) D. (*+1)(x*-3)

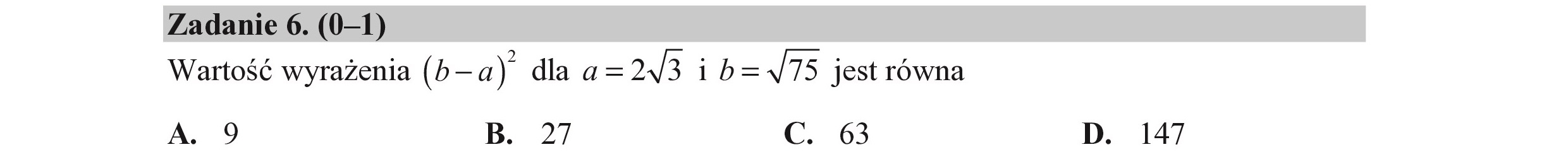
Zadanie 6. (0—1) Wartość wyrażenia (b— a) dla a=243 i b=</T5 jestrówna A. 9 B. 27 C. 63 D. 147

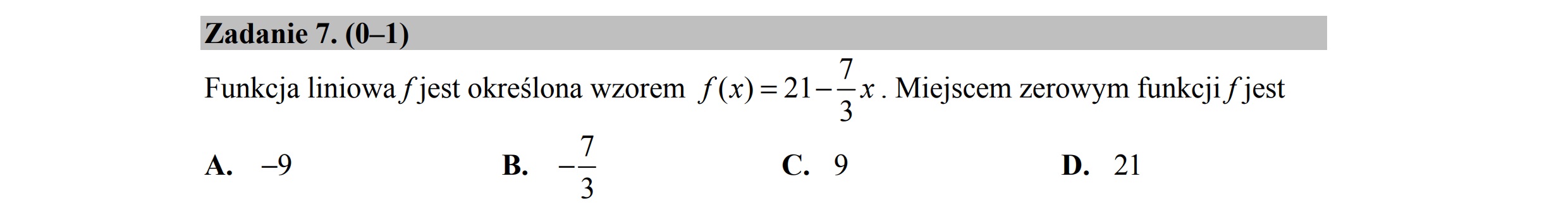
Zadanie 7. (0—1) Funkcja liniowa f jest określona wzorem f(x) =21— zx . Miejscem zerowym funkcji / jest A. 9 B. -3 c 9 D. 21


Zadanie 8. (0—1) . xty=l RE 2. . . Rozwiązaniem układu równań | * z niewiadomymi x i y jest para liczb dodatnich. X-p= Wynika stąd, że A. b<-l B. b=—l C. -1<b<l D. b2l


Zadanie 9. (0—1) Funkcja kwadratowa f jest określona wzorem f(x)=x'+bx+c oraz f(-1)=/f(3)=1. Współczynnik b jest równy A. 2 B. —I c. 0 D. 3

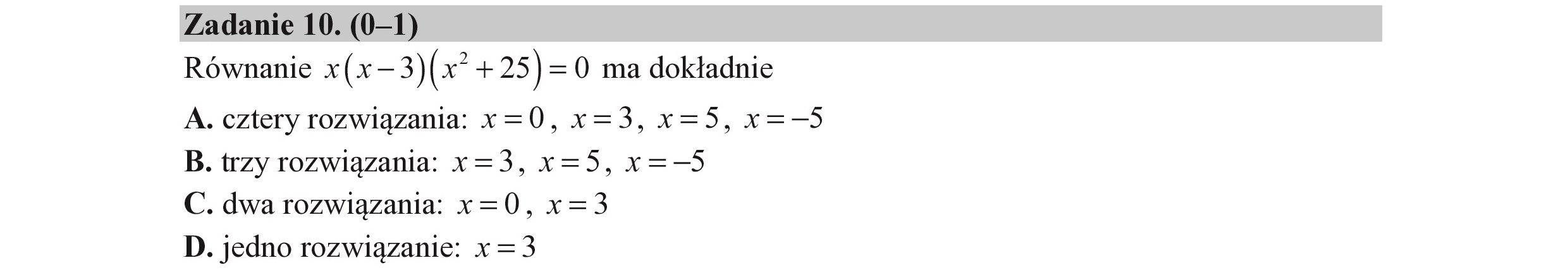
Zadanie 10. ra 1) Równanie x(x-3 )(e +25)=0 dokładnie A. cztery rozwiązania: x=0, x=3, x=5, x=—5 B. trzy rozwiązania: x=3, x=5, x= 5 -5, C. dwa rozwiązania: x=0, x=3 D. jedno rozwiązanie: x = s


Zadanie 11. (0—1) Funkcja kwadratowa f jest określona wzorem f(x) =(x-3)(7-x). Wierzchołek paraboli będącej wykresem funkcji fnależy do prostej o równaniu A. y=-5 B. y=5 C. y=-—4 D. y=4


Zadanie 12. (0—1) Punkt 4=(2017,0) należy do wykresu funkcji f określonej wzorem A. f(x)=(x+2017) B. f(x)=x —2017 C. f(x)=(x+2017)(x-—2017) D. /(x)=x +2017


Zadanie 13. (0—1) W ciągu arytmetycznym (a,), określonym dla n>l, spełniony jest warunek 2a, =a, +a, +1. Różnica r tego ciągu jest równa A. 0 B. Ka: W |< . 3

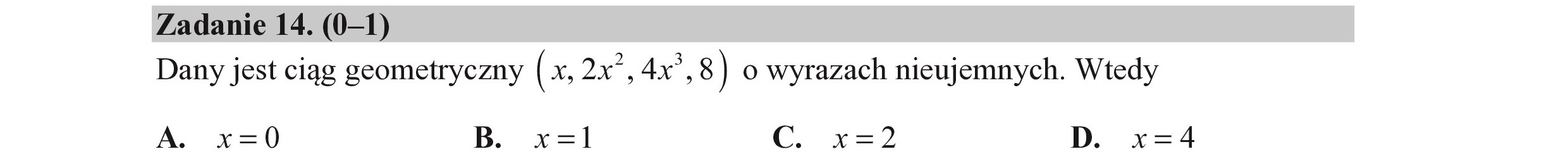
Zadanie 14. (0-1) Dany jest ciąg geometryczny (x. 2% ,4X , 8) o wyrazach nieujemnych. Wtedy A. x=0 B. x=l1 CC. x=2 D. x=4


Zadanie 15. (0—1) . ! 12 ; " , Kąt a jest ostry 1 tga = g” Wówczas sina jest równy 3 B 12 5 A. — : c. — 17 17 13 I2 13


Zadanie 16. (0—1) W okręgu o środku O dany jest kąt wpisany ABC o mierze 20? (patrz rysunek). Miara kąta CAO jest równa A. 859 B. 707 c. 80? D. 757


Zadanie 17. (0—1) Odcinek BD jest zawarty w dwusiecznej kąta ostrego ABC trójkąta prostokątnego, w którym przyprostokątne AC 1 BC mają długości odpowiednio 5 13. B D 3 a A C D 5 Wówczas miara g kąta DBC spełnia warunek A. 20<g<257 B. 25<g<307 C. 300 <p<357 D. 35*<g<407

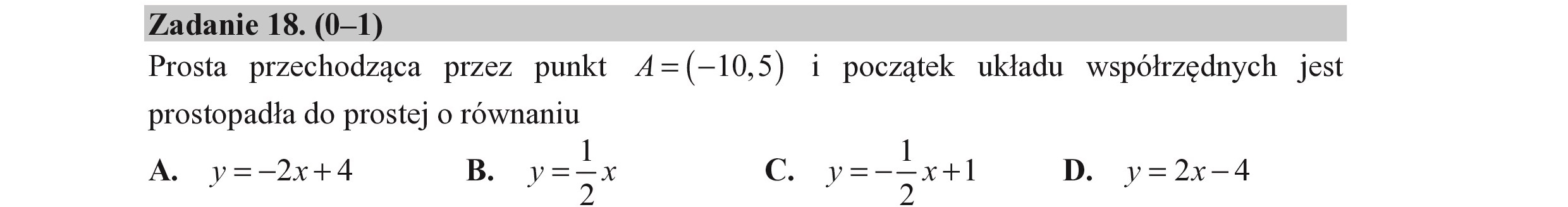
Zadanie 18. (0—1) Prosta przechodząca przez punkt A=(-10,5) i początek układu współrzędnych jest prostopadła do prostej o równaniu A. y=-2x+4 B. y=żx c. p=-zak1 D. v=2x-4


Zadanie 19. (0—1) Punkty A=(-21,11) i B=(3,17) są końcami odcinka AB. Obrazem tego odcinka w symetrii względem osi Ox układu współrzędnych jest odcinek AB”. Środkiem odcinka 4'B' jest punkt o współrzędnych A. (-9,—14) B. (-9,14) c. (9,—14) D. (9,14)


Zadanie 20. (0—1) . . Pp? AA . 5 (Es14 Trójkąt ABC jest podobny do trójkąta ABC wskali > , przy czym |4B| = G AB|. Stosunek pola trójkąta ABC do pola trójkąta 4 BC” jest równy A. — B. JE p. > 23 5 2 4


Zadanie 21. (0—1) Pole koła opisanego na trójkącie równobocznym jest równe z . Długość boku tego trójkąta jest równa A. A B. z c. Ju D. 3a


Zadanie 22. (0—1) Pole trójkąta prostokątnego ABC, przedstawionego na rysunku, jest równe (e


Zadanie 23. (0—1) Długość przekątnej sześcianu jest równa 6 . Stąd wynika, że pole powierzchni całkowitej tego sześcianu jest równe A. 72 B. 48 c. 152 D. 108


Zadanie 24. (0—1) Pole powierzchni bocznej walca jest równe lóx, a promień jego podstawy ma długość 2. Wysokość tego walca jest równa A. 4 B. 8 C. 4n D. 8n


Zadanie 25. (0—1) Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania pary liczb, których iloczyn jest większy od 20, jest równe A. — B. — c. 2 p. > 6 36 A 8

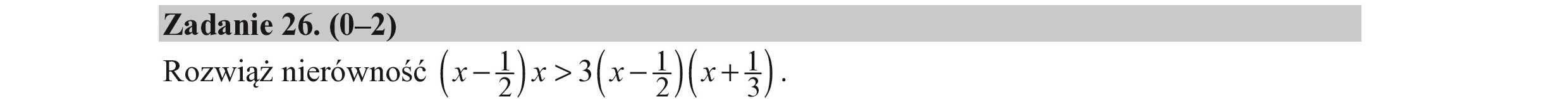
Zadanie 26. (0—2) Rozwiąż nierówność (x- ) 1) x > 3(x- p 1) (x de 1).

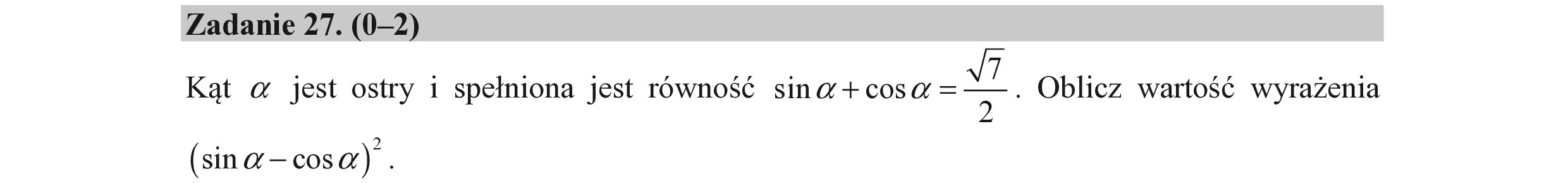
Zadanie 27. (0—2) Kąt a jest ostry i spełniona jest równość sina + DARERE Ty + Oblicz wartość wyrażenia (sin 2 — cos a) .


Zadanie 28. (0—2) Dwusieczna kąta ostrego ABC przecina przyprostokątną AC trójkąta prostokątnego ABC w punkcie D. B Udowodnij, że jeżeli |4D|=|BD „to [EP|->-|BD|.


Zadanie 29. (0-2) Wykaż, że prawdziwa jest nierówność y 2 p J (1,5) < 62 i


Zadanie 30. (0—2) Suma trzydziestu początkowych wyrazów ciągu arytmetycznego (a, ) , określonego dla n> l, jest równa 30. Ponadto a., = 30. Oblicz różnicę tego ciągu.


Zadanie 31. (0—2) Ze zbioru liczb 11, 2, 3, 4, 5, 6, 7,8,9,10,11, 12, 13, 14, 15) losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę (a, b), gdzie a jest wynikiem pierwszego losowania, b jest wynikiem drugiego losowania. Oblicz, ile jest wszystkich par (a, b) takich, że iloczyn a:b jest liczbą parzystą.


Zadanie 32. (0—4) Ramię trapezu równoramiennego ABCD ma długość 426. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2: 3. Oblicz pole tego trapezu.


Zadanie 33. (0—4) Punkty A=(-2,—8) i B=(14,—8) są wierzchołkami trójkąta równoramiennego ABC, w którym |4B8|=|AC|. Wysokość AD tego trójkąta jest zawarta w prostej o równaniu l . . . y= zg 7. Oblicz współrzędne wierzchołka C tego trójkąta.


Zadanie 34. (0—5) Podstawą graniastosłupa prostego ABCDA BCD” jest romb ABCD. Przekątna AC tego graniastosłupa ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem 307, a przekątna BD” jest nachylona do tej płaszczyzny pod kątem 45”. Oblicz pole powierzchni całkowitej tego graniastosłupa. D






























