MATEMATYKA 2016 MAJ MATURA STARA PODSTAWOWA

Zadanie 1. (I pkt) Dla każdej dodatniej liczby a iloraz —— A. a* B. a” -2,6 3 3 jest równy C. a —1,3 1,3


Zadanie 2. (I pkt) Liczba log złe2 ) jest równa 3 A. — B. 2 2 blu


Zadanie 3. (I pkt) Liczby a i c są dodatnie. Liczba b stanowi 48% liczby a oraz 32% liczby c. Wynika stąd, że A. c=lL5a B. c=l6a C. c=0,8a D. c=0,lba


Zadanie 4. (I pkt) Równość (242 — a) =17-12/2 jest prawdziwa dla A. a=3 B. a=l c. a=—2

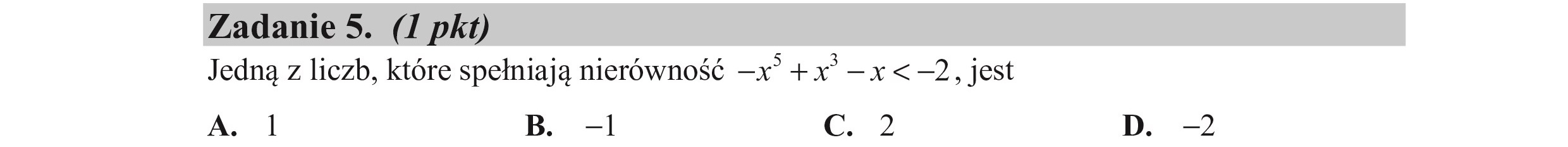
Zadanie 5. (I pkt) Jedną z liczb, które spełniają nierówność —x +x —x < —2, jest A. 1 B. —1 C. 2

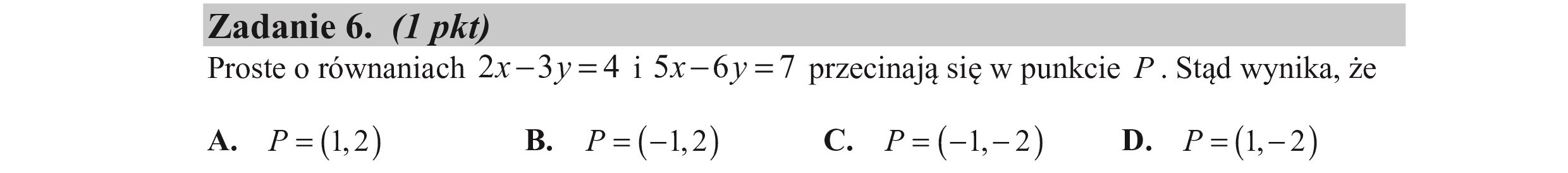
Zadanie 6. (I pkt) Proste o równaniach 2x—3y=4 i 5x—6y=7 przecinają się w punkcie P. Stąd wynika, że A. P=(1,2) B. P=(-1,2) C. P=(-1-2) DD. P=(1,-2)

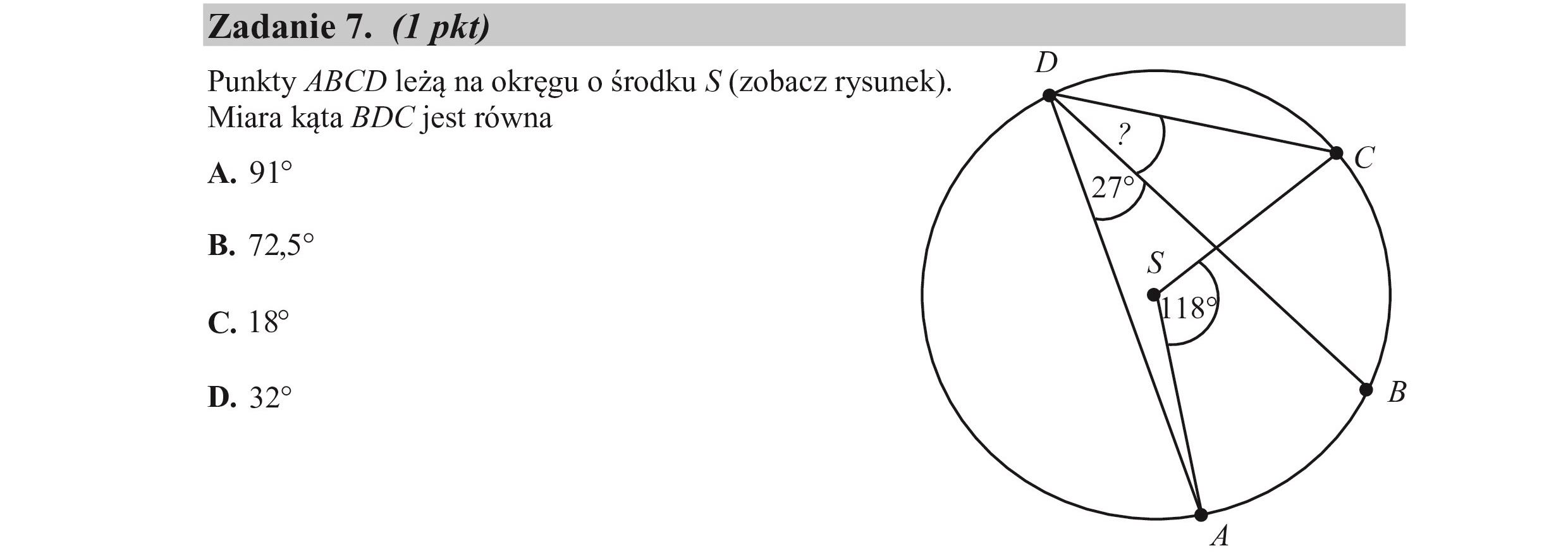
Zadanie 7. (I pkt) Punkty ABCD leżą na okręgu o środku S$ (zobacz rysunek). Miara kąta BDC jest równa A. 91? B. 72,3" C. 187 D. 32”


Zadanie 8. (I pkt) Dana jest funkcja liniowa f/(x)= żx+ 6. Miejscem zerowym tej funkcji jest liczba A. 8 B. 6 CG =Ó D. —8


Zadanie 9. (I pkt) — =3,gdzie xź+—5, Równanie wymierne X nie ma rozwiązań rzeczywistych. ma dokładnie jedno rozwiązanie rzeczywiste. ma dokładnie dwa rozwiązania rzeczywiste. SOPP ma dokładnie trzy rozwiązania rzeczywiste.

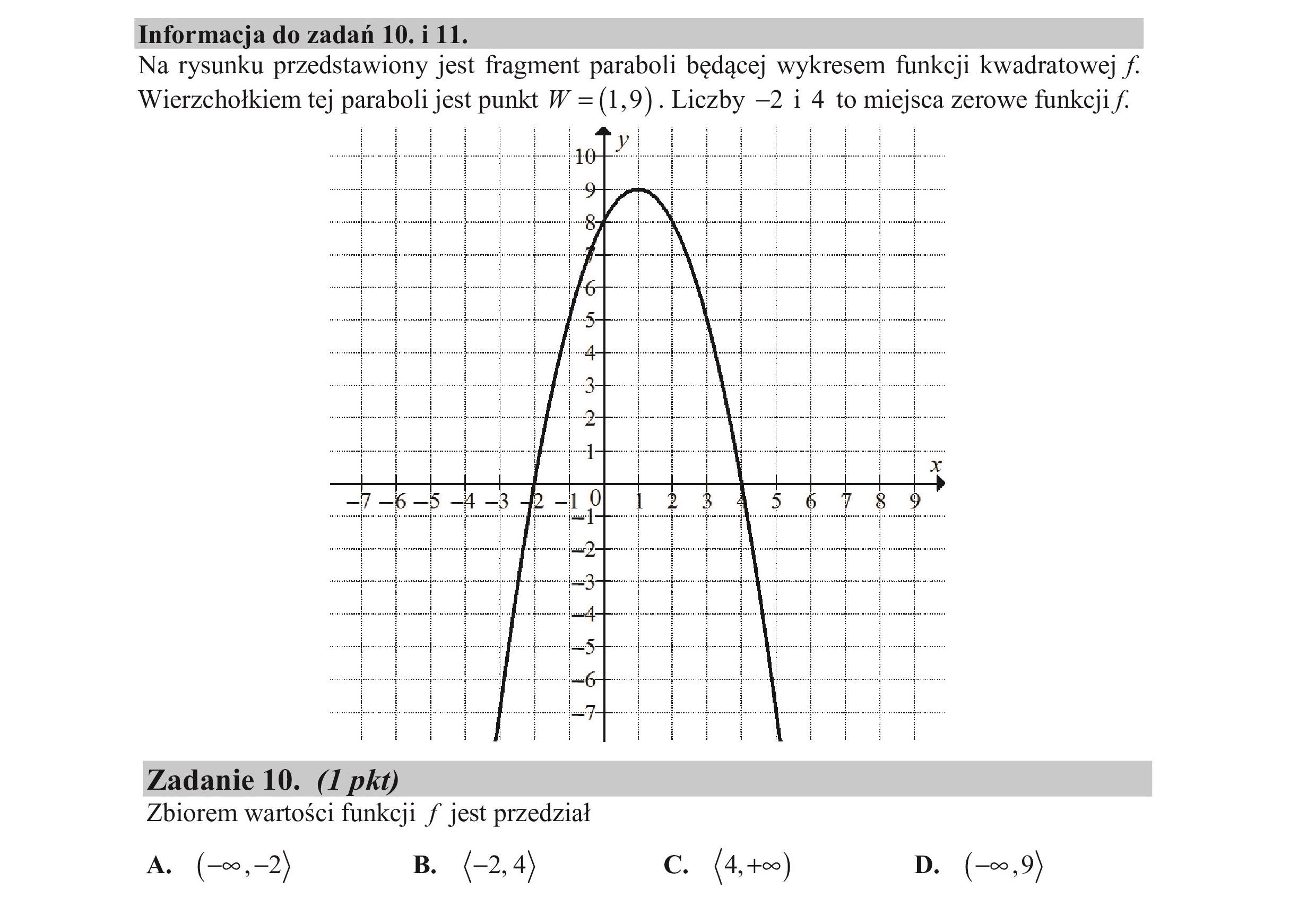
Informacja do zadań 10.i 11. Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej f. Wierzchołkiem tej paraboli jest punkt W =(1,9). Liczby —2 i 4 to miejsca zerowe funkcji f. y) Zadanie 10. (I pkt) Zbiorem wartości funkcji / jest przedział A. (—0,—2) B. (-2,4) C. (4,+eo) D. (—,9)

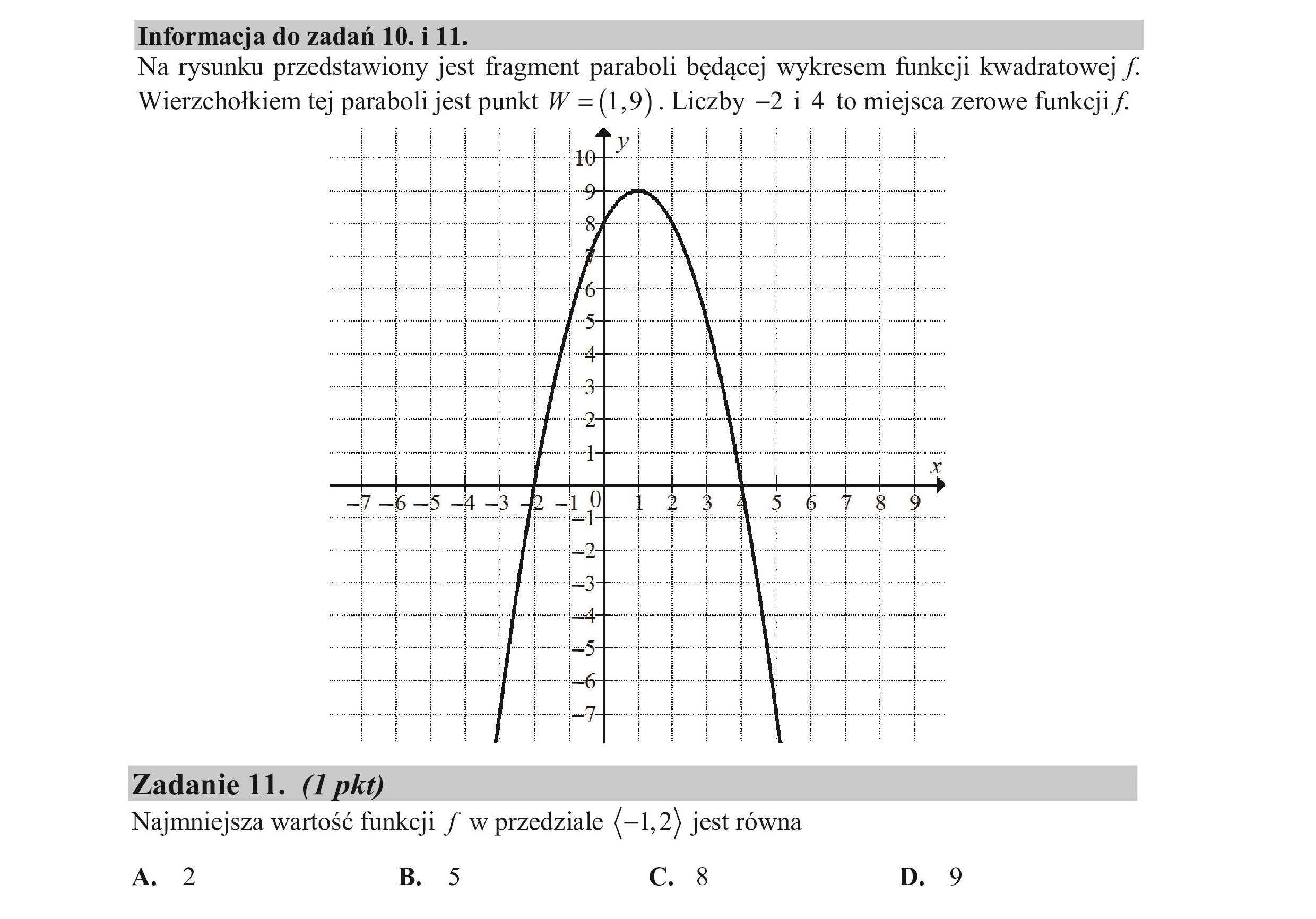
Informacja do zadań 10.i 11. Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej f. Wierzchołkiem tej paraboli jest punkt W =(1,9). Liczby —2 i 4 to miejsca zerowe funkcji f. a. Zadanie 11. (I pkt) Najmniejsza wartość funkcji f/ w przedziale (-1,2) jest równa A. 2 B. 5 Cc. 8 D. 9


Zadanie 12. (I pkt) 3 Funkcja f określona jest wzorem f(x)= Rh i dla każdej liczby rzeczywistej x. Wtedy M /(-3B) jest równa 3 3 A. AB B. -3 SE p. 3 2 5 5 2

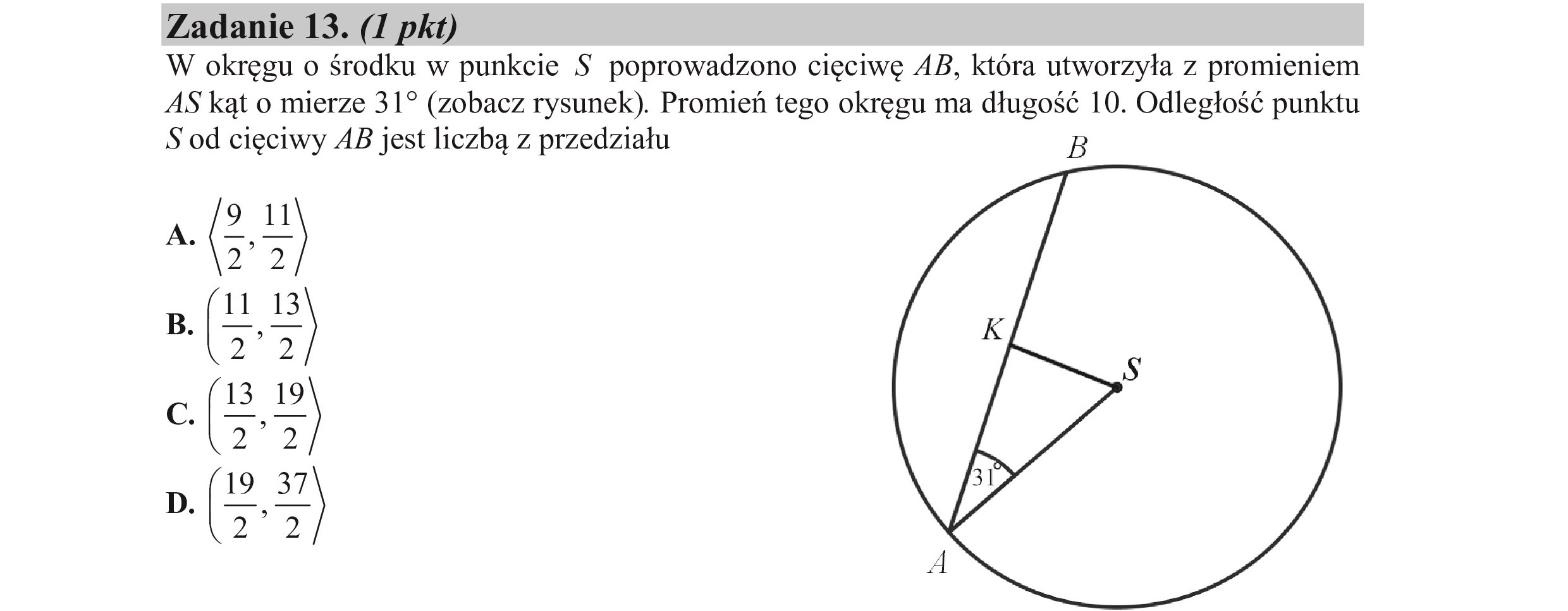
Zadanie 13. (I pkt) W okręgu o środku w punkcie $ poprowadzono cięciwę AB, która utworzyła z promieniem AS kąt o mierze 31? (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu Ś od cięciwy 4B jest liczbą z przedziału NE 22 B NSE 2 2 c.(3,19 2 2 ».(5,37) 22

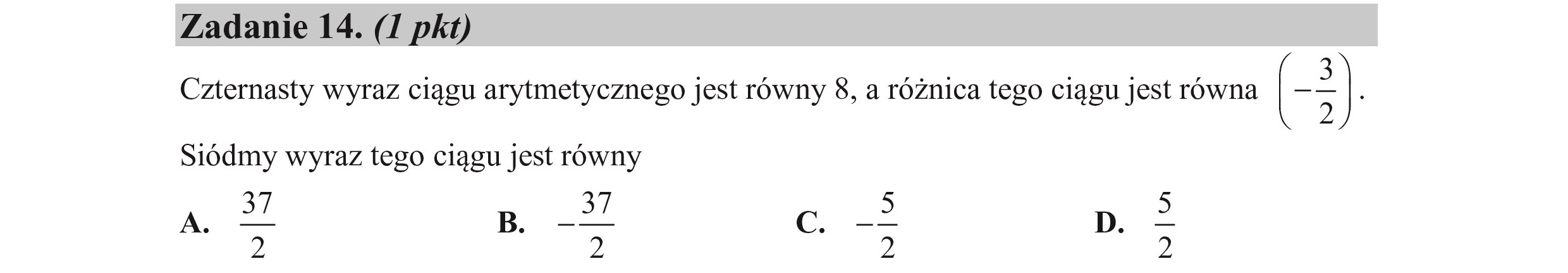
Zadanie 14. (I pkt) Czternasty wyraz ciągu arytmetycznego jest równy 8, a różnica tego ciągu jest równa (3) z Siódmy wyraz tego ciągu jest równy c B. -— G — D A. 3 2 2 2 2


Zadanie 15. (I pkt) Ciąg (x, 2x+3,4x+3) jest geometryczny. Pierwszy wyraz tego ciągu jest równy A. -—4 B. I c. 0 D. -1

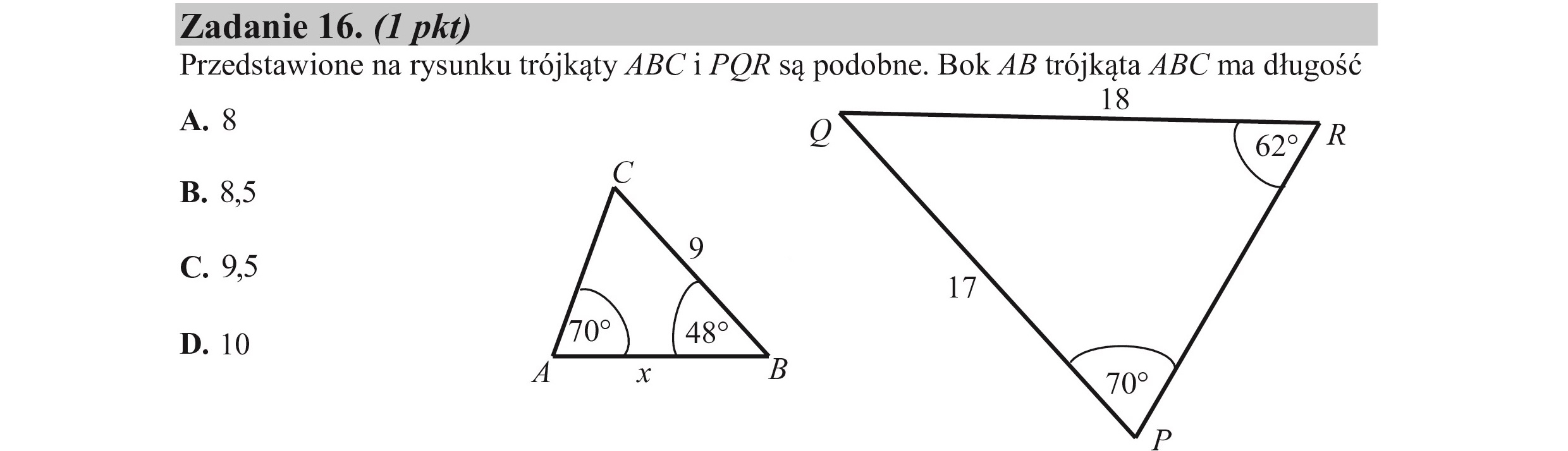
Zadanie 16. (I pkt) Przedstawione na rysunku trójkąty ABC i PQOR są podobne. Bok 4B trójkąta ABC ma długość 18 A. 8 O G/ R B. 8,5 Ń C. 9,5 17 D. 10 fo) 487

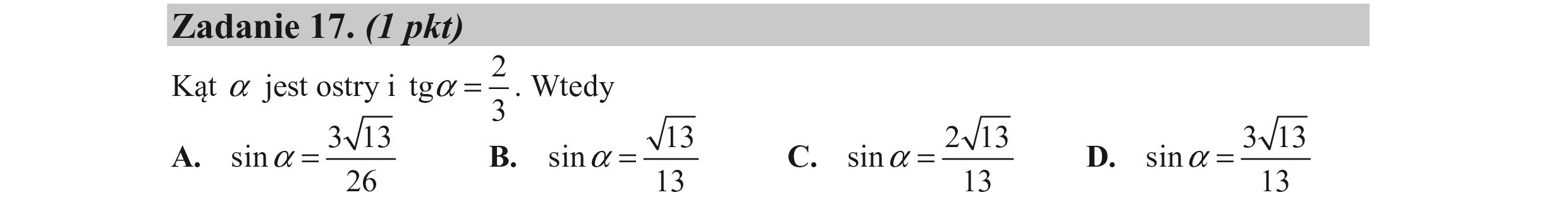
Zadanie 17. (I pkt) Kąt a jest ostry i tga= z Wtedy 3/13 6 A. sna0= B. sna=


Zadanie 18. (I pkt) Z odcinków o długościach: 5, 2a+1, a—l można zbudować trójkąt równoramienny. Wynika stąd, że A. a=6 B. a=4 C. a a= I LO 7

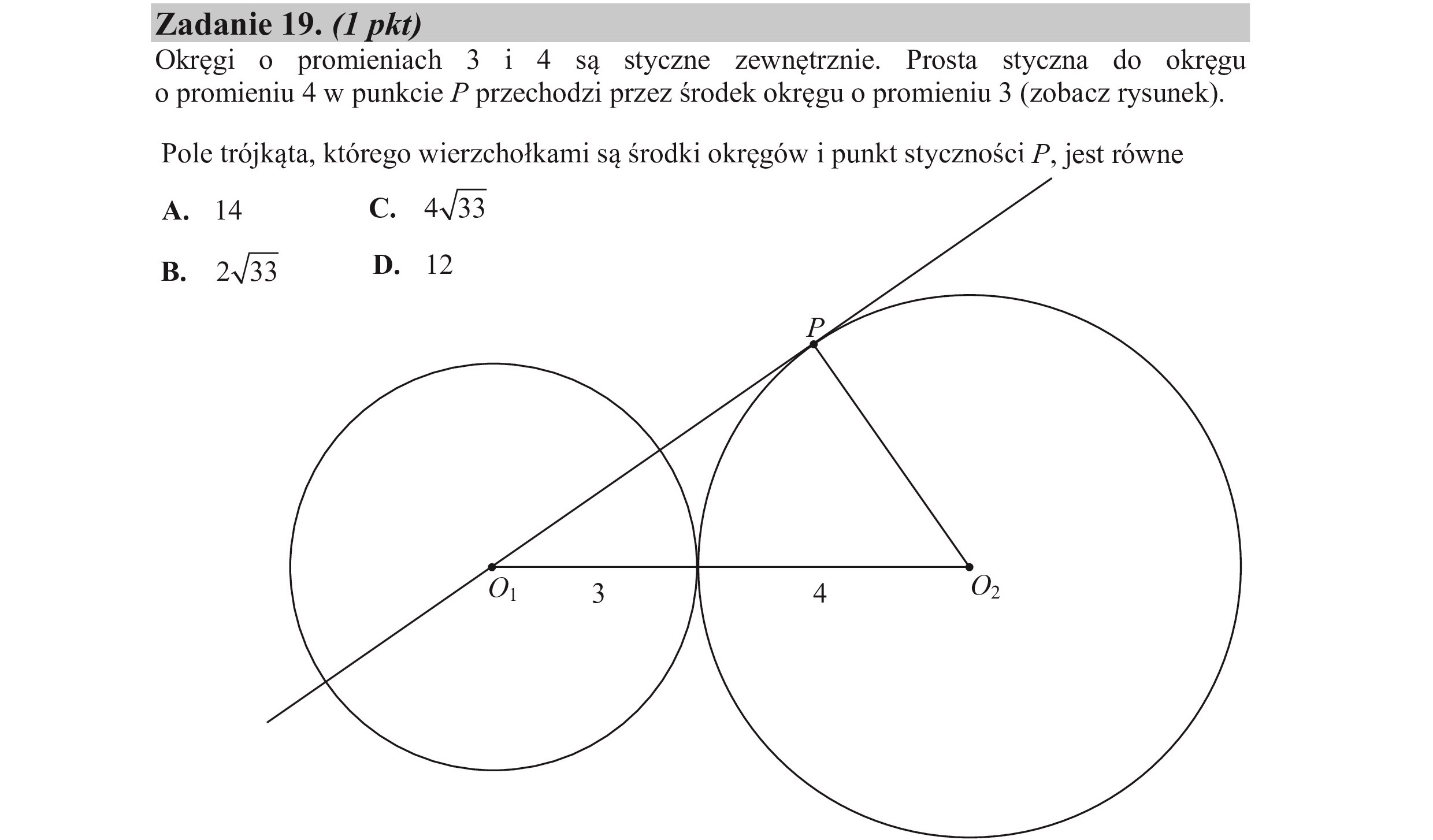
Zadanie 19. (I pkt) Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie P przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek). Pole trójkąta, którego wierzchołkami są środki okręgów 1 punkt styczności P, jest równe A. 14 C. 4433 B. 2433 D. 12

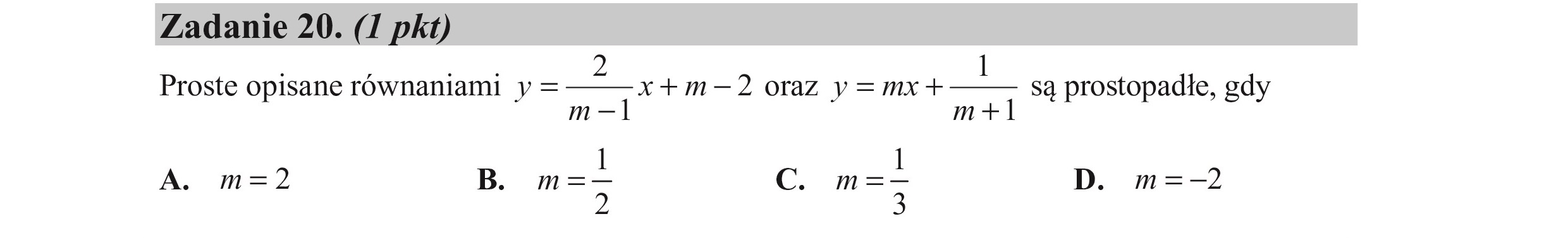
Zadanie 20. (I pkt) Proste opisane równaniami y= x+m—2 oraz y=mx+ d i są prostopadłe, gdy n + m —1 A. m=2 B. |" Cc. „a D. m=— p 3


Zadanie 21. (I pkt) W układzie współrzędnych dane są punkty A=(a,6) oraz B=(7,b). Środkiem odcinka AB jest punkt M =(3, 4). Wynika stąd, że A. a=5ib=$5 B. a=-lib=2 C. a=4i1b=10 D. a=-4i1b=—2


Zadanie 22. (I pkt)
Rzucamy trzy razy symetryczną monetą. Niech p oznacza prawdopodobieństwo otrzymania
dokładnie dwóch orłów w tych trzech rzutach. Wtedy
A. 0

Zadanie 23. (I pkt) Kąt rozwarcia stożka ma miarę 120”, a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa A. 361 B. lsn c. 24m D. 8n

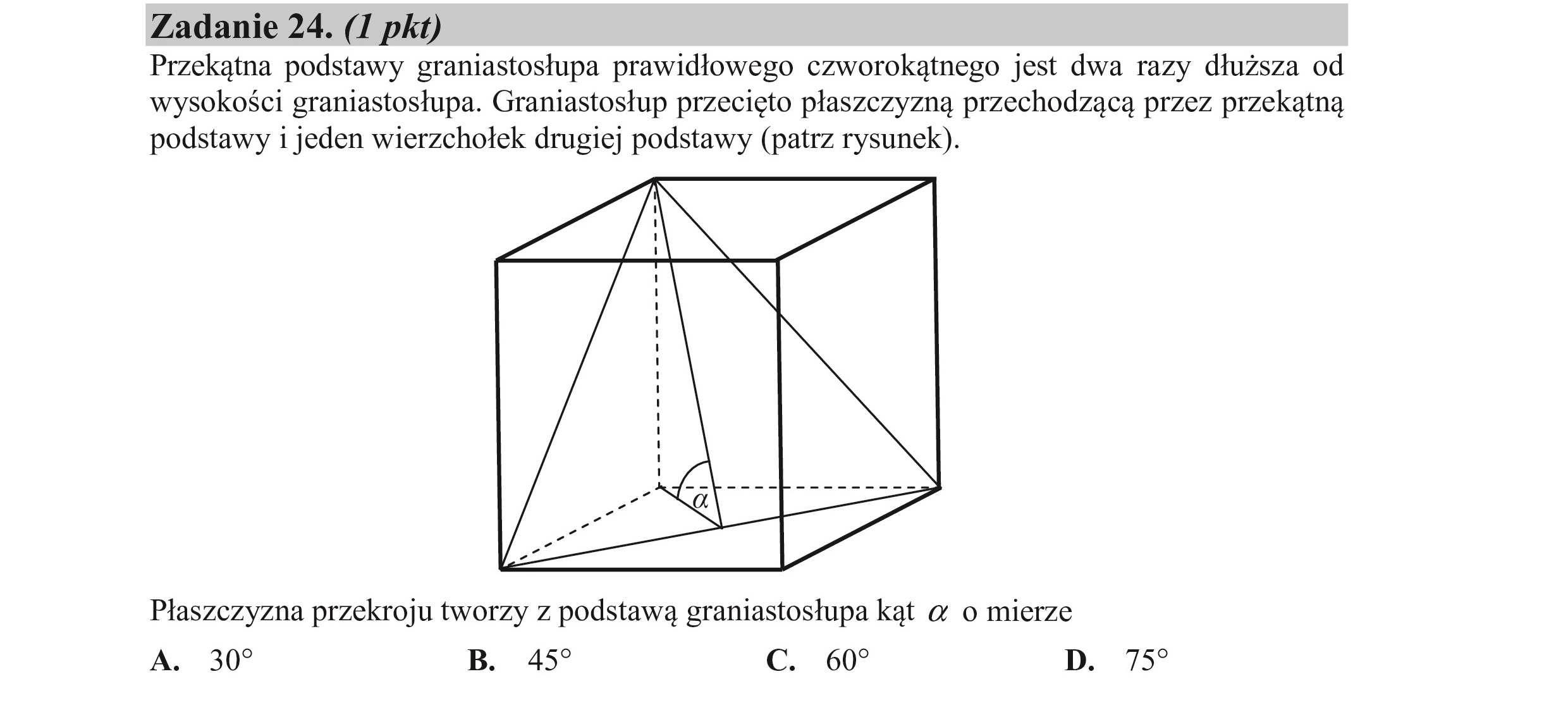
Zadanie 24. (I pkt) Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek). Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt 2 o mierze A. 30? B. 457 c. 60? D. 757


Zadanie 25. (I pkt) Średnia arytmetyczna sześciu liczb naturalnych: 31, 16, 25, 29, 27, x, jest równa ę Mediana tych liczb jest równa A. 26 B. 27 Cc. 28 D. 29


Rozwiąż nierówność 2x +5x-3>0.


Rozwiąż równanie x +3x +2x+6=0.


Zadanie 28. (2 pkt) . + PE s_Ą ! -; PE Kąt Q jest ostry i (sin A + COS a) = z” Oblicz wartość wyrażenia Sina :cosa.

Zadanie 29. (2 pkt)
Dany jest trójkąt prostokątny ABC. Na przyprostokątnych AC i AB tego trójkąta obrano
odpowiednio punkty D i G. Na przeciwprostokątnej BC wyznaczono punkty £ i F takie, że
|

Zadanie 30. (2 pkt) Ciąg (a,) jest określony wzorem a, = 2n'+2n dla n>1. Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.


Zadanie 31. (2 pkt) W skończonym ciągu arytmetycznym (a,) pierwszy wyraz a, jest równy 7 oraz ostatni wyraz a, jest równy 89. Suma wszystkich wyrazów tego ciągu jest równa 2016. Oblicz, ile wyrazów ma ten ciąg.


Zadanie 32. (4 pkt) Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch pozostałych kątów, które różnią się o 50”. Oblicz kąty tego trójkąta.


Zadanie 33. (5 pkt) Grupa znajomych wyjeżdżających na biwak wynajęła bus. Koszt wynajęcia busa jest równy 960 złotych i tę kwotę rozłożono po równo pomiędzy uczestników wyjazdu. Do grupy wyjeżdżających dołączyło w ostatniej chwili dwóch znajomych. Wtedy koszt wyjazdu przypadający na jednego uczestnika zmniejszył się o 16 złotych. Oblicz, ile osób wyjechało na biwak.


Zadanie 34. (4 pkt) Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie równa 30. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.

MATEMATYKA 2016 MAJ MATURA STARA PODSTAWOWA

Zadanie 1. (I pkt) Dla każdej dodatniej liczby a iloraz —— A. a* B. a” -2,6 3 3 jest równy C. a —1,3 1,3


Zadanie 2. (I pkt) Liczba log złe2 ) jest równa 3 A. — B. 2 2 blu


Zadanie 3. (I pkt) Liczby a i c są dodatnie. Liczba b stanowi 48% liczby a oraz 32% liczby c. Wynika stąd, że A. c=lL5a B. c=l6a C. c=0,8a D. c=0,lba


Zadanie 4. (I pkt) Równość (242 — a) =17-12/2 jest prawdziwa dla A. a=3 B. a=l c. a=—2

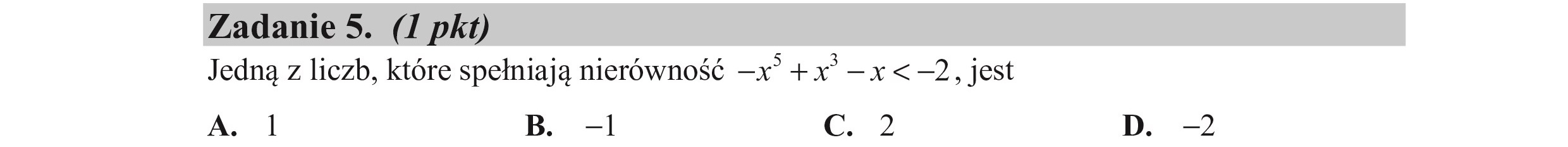
Zadanie 5. (I pkt) Jedną z liczb, które spełniają nierówność —x +x —x < —2, jest A. 1 B. —1 C. 2

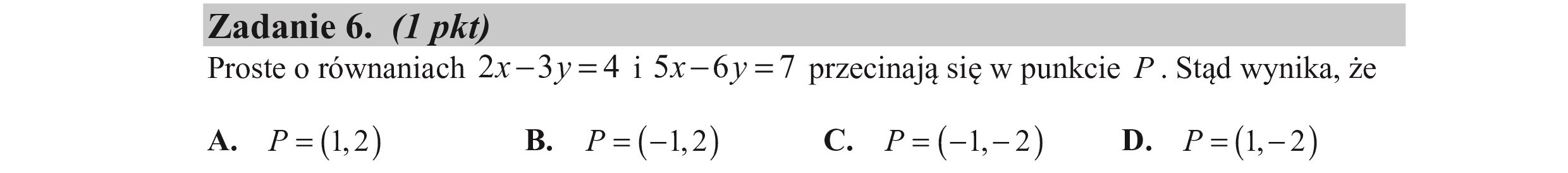
Zadanie 6. (I pkt) Proste o równaniach 2x—3y=4 i 5x—6y=7 przecinają się w punkcie P. Stąd wynika, że A. P=(1,2) B. P=(-1,2) C. P=(-1-2) DD. P=(1,-2)


Zadanie 7. (I pkt) Punkty ABCD leżą na okręgu o środku S$ (zobacz rysunek). Miara kąta BDC jest równa A. 91? B. 72,3" C. 187 D. 32”


Zadanie 8. (I pkt) Dana jest funkcja liniowa f/(x)= żx+ 6. Miejscem zerowym tej funkcji jest liczba A. 8 B. 6 CG =Ó D. —8


Zadanie 9. (I pkt) — =3,gdzie xź+—5, Równanie wymierne X nie ma rozwiązań rzeczywistych. ma dokładnie jedno rozwiązanie rzeczywiste. ma dokładnie dwa rozwiązania rzeczywiste. SOPP ma dokładnie trzy rozwiązania rzeczywiste.


Informacja do zadań 10.i 11. Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej f. Wierzchołkiem tej paraboli jest punkt W =(1,9). Liczby —2 i 4 to miejsca zerowe funkcji f. y) Zadanie 10. (I pkt) Zbiorem wartości funkcji / jest przedział A. (—0,—2) B. (-2,4) C. (4,+eo) D. (—,9)


Informacja do zadań 10.i 11. Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej f. Wierzchołkiem tej paraboli jest punkt W =(1,9). Liczby —2 i 4 to miejsca zerowe funkcji f. a. Zadanie 11. (I pkt) Najmniejsza wartość funkcji f/ w przedziale (-1,2) jest równa A. 2 B. 5 Cc. 8 D. 9


Zadanie 12. (I pkt) 3 Funkcja f określona jest wzorem f(x)= Rh i dla każdej liczby rzeczywistej x. Wtedy M /(-3B) jest równa 3 3 A. AB B. -3 SE p. 3 2 5 5 2


Zadanie 13. (I pkt) W okręgu o środku w punkcie $ poprowadzono cięciwę AB, która utworzyła z promieniem AS kąt o mierze 31? (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu Ś od cięciwy 4B jest liczbą z przedziału NE 22 B NSE 2 2 c.(3,19 2 2 ».(5,37) 22

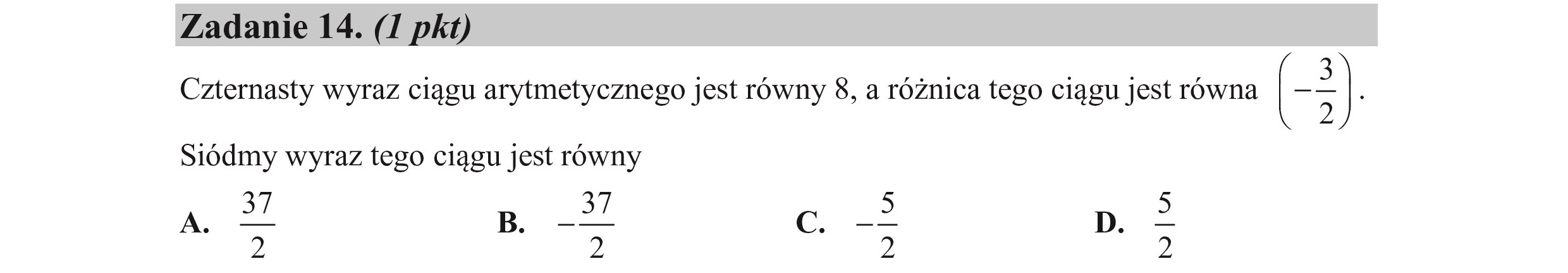
Zadanie 14. (I pkt) Czternasty wyraz ciągu arytmetycznego jest równy 8, a różnica tego ciągu jest równa (3) z Siódmy wyraz tego ciągu jest równy c B. -— G — D A. 3 2 2 2 2


Zadanie 15. (I pkt) Ciąg (x, 2x+3,4x+3) jest geometryczny. Pierwszy wyraz tego ciągu jest równy A. -—4 B. I c. 0 D. -1


Zadanie 16. (I pkt) Przedstawione na rysunku trójkąty ABC i PQOR są podobne. Bok 4B trójkąta ABC ma długość 18 A. 8 O G/ R B. 8,5 Ń C. 9,5 17 D. 10 fo) 487

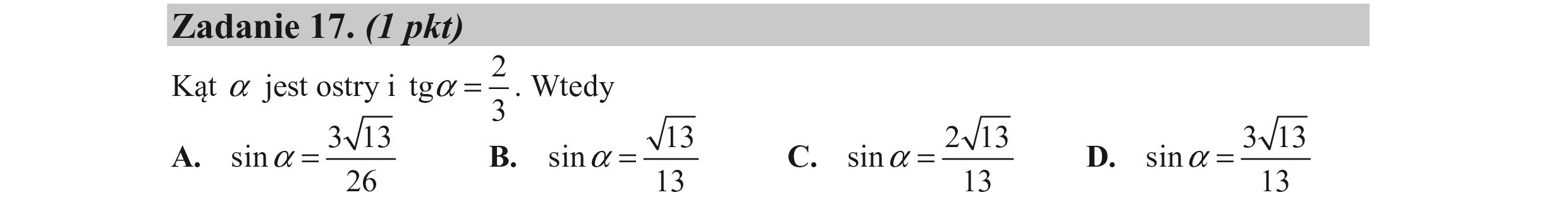
Zadanie 17. (I pkt) Kąt a jest ostry i tga= z Wtedy 3/13 6 A. sna0= B. sna=


Zadanie 18. (I pkt) Z odcinków o długościach: 5, 2a+1, a—l można zbudować trójkąt równoramienny. Wynika stąd, że A. a=6 B. a=4 C. a a= I LO 7


Zadanie 19. (I pkt) Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie P przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek). Pole trójkąta, którego wierzchołkami są środki okręgów 1 punkt styczności P, jest równe A. 14 C. 4433 B. 2433 D. 12

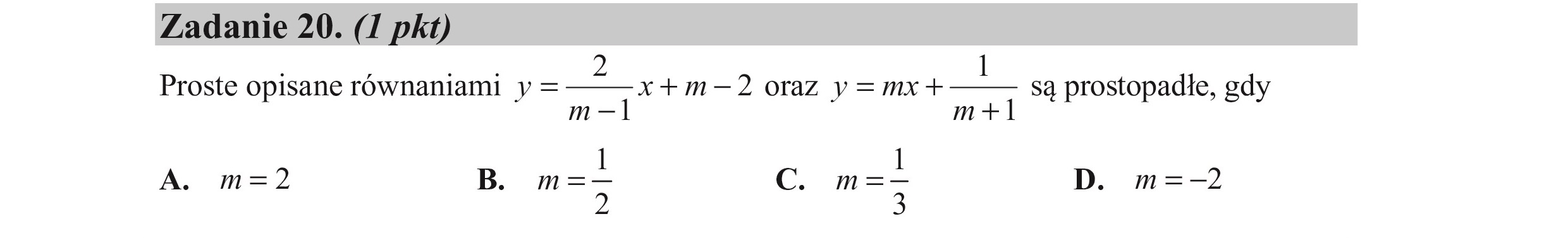
Zadanie 20. (I pkt) Proste opisane równaniami y= x+m—2 oraz y=mx+ d i są prostopadłe, gdy n + m —1 A. m=2 B. |" Cc. „a D. m=— p 3


Zadanie 21. (I pkt) W układzie współrzędnych dane są punkty A=(a,6) oraz B=(7,b). Środkiem odcinka AB jest punkt M =(3, 4). Wynika stąd, że A. a=5ib=$5 B. a=-lib=2 C. a=4i1b=10 D. a=-4i1b=—2


Zadanie 22. (I pkt) Rzucamy trzy razy symetryczną monetą. Niech p oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy A. 0<p<0,2 B. 0,2<p<0,35 (C. 0,35<p<Q,5 D. 0,5<p<l


Zadanie 23. (I pkt) Kąt rozwarcia stożka ma miarę 120”, a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa A. 361 B. lsn c. 24m D. 8n


Zadanie 24. (I pkt) Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek). Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt 2 o mierze A. 30? B. 457 c. 60? D. 757


Zadanie 25. (I pkt) Średnia arytmetyczna sześciu liczb naturalnych: 31, 16, 25, 29, 27, x, jest równa ę Mediana tych liczb jest równa A. 26 B. 27 Cc. 28 D. 29


Rozwiąż nierówność 2x +5x-3>0.


Rozwiąż równanie x +3x +2x+6=0.


Zadanie 28. (2 pkt) . + PE s_Ą ! -; PE Kąt Q jest ostry i (sin A + COS a) = z” Oblicz wartość wyrażenia Sina :cosa.


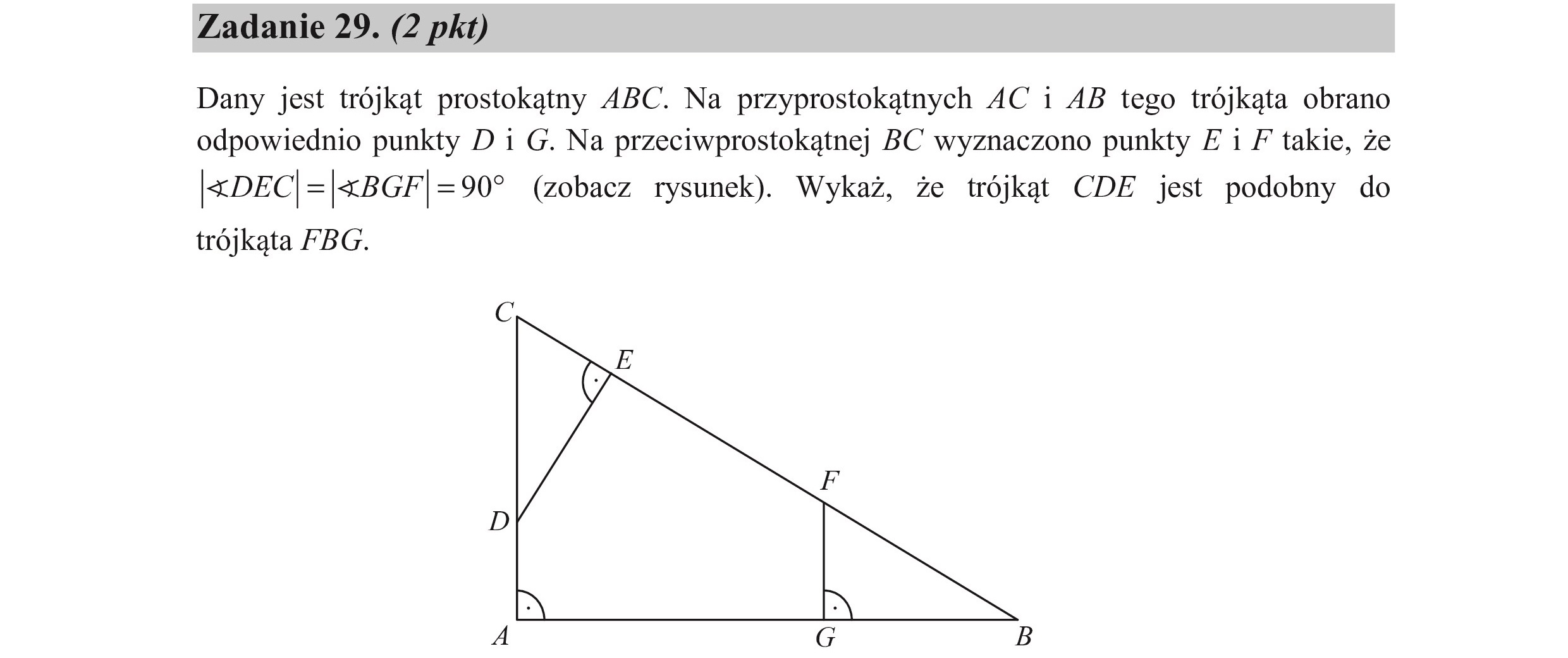
Zadanie 29. (2 pkt) Dany jest trójkąt prostokątny ABC. Na przyprostokątnych AC i AB tego trójkąta obrano odpowiednio punkty D i G. Na przeciwprostokątnej BC wyznaczono punkty £ i F takie, że |<DEC| =|«BGF | =90” (zobacz rysunek). Wykaż, że trójkąt CDE jest podobny do trójkąta FBG.


Zadanie 30. (2 pkt) Ciąg (a,) jest określony wzorem a, = 2n'+2n dla n>1. Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.


Zadanie 31. (2 pkt) W skończonym ciągu arytmetycznym (a,) pierwszy wyraz a, jest równy 7 oraz ostatni wyraz a, jest równy 89. Suma wszystkich wyrazów tego ciągu jest równa 2016. Oblicz, ile wyrazów ma ten ciąg.


Zadanie 32. (4 pkt) Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch pozostałych kątów, które różnią się o 50”. Oblicz kąty tego trójkąta.


Zadanie 33. (5 pkt) Grupa znajomych wyjeżdżających na biwak wynajęła bus. Koszt wynajęcia busa jest równy 960 złotych i tę kwotę rozłożono po równo pomiędzy uczestników wyjazdu. Do grupy wyjeżdżających dołączyło w ostatniej chwili dwóch znajomych. Wtedy koszt wyjazdu przypadający na jednego uczestnika zmniejszył się o 16 złotych. Oblicz, ile osób wyjechało na biwak.


Zadanie 34. (4 pkt) Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie równa 30. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.






























