MATEMATYKA 2015 SIERPIEN POPRAWKOWA STARA PODSTAWOWA

Zadanie 1. (I pkt) l : Ż . a+b Niech a= 3 b= zy Wtedy wartość wyrażenia ka A, B. 2 5 jest równa b |w


Zadanie 2. (I pkt) Cenę pewnego towaru obniżano dwukrotnie, za każdym razem o 20%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką A. 040%. B. o 36%. GC. 632%. D. o 28%.


Zadanie 3. (I pkt) 12 95 Liczba —— 150 jest równa A. 25 B. ą7 ą3 23 27


Zadanie 4. (I pkt) W rozwinięciu dziesiętnym ułamka = na trzydziestym miejscu po przecinku stoi cyfra A. 7 B. I G 2 D. 4


Zadanie 5. (I pkt) Wskaż największą liczbę całkowitą spełniającą nierówność 47 3<0. A. 5 B. 6 Cc. 7 D. 8

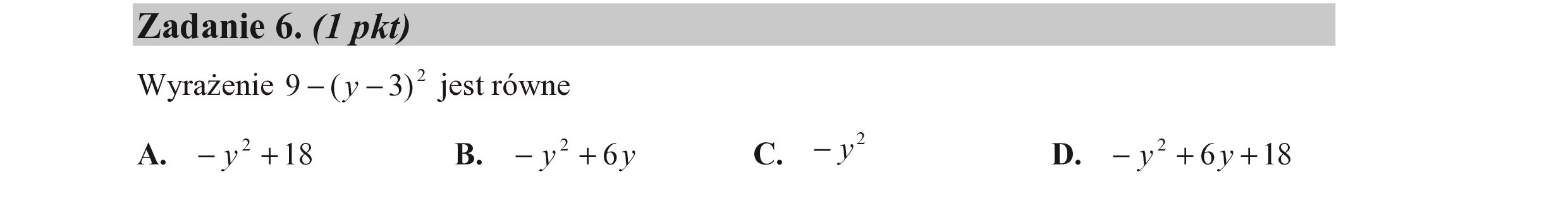
Zadanie 6. (I pkt) Wyrażenie 9 — (y —3)” jest równe J A. —y*+18 B. -y'+ó6y c. "FP D. -y'+6y+18


Zadanie 7. (I pkt) = R 1 25... Iloczyn liczb spełniających równanie kg 4 =() jest równy A. 6 B. —5 LC. 5


Zadanie 8. (I pkt) Wierzchołek paraboli będącej wykresem funkcji kwadratowej y = f(x) ma współrzędne (2,2). Wówczas wierzchołek paraboli będącej wykresem funkcji g(x)=/(x+2) ma współrzędne A. (0,2) B. (4,2) c. (2,0) D. (2,4)

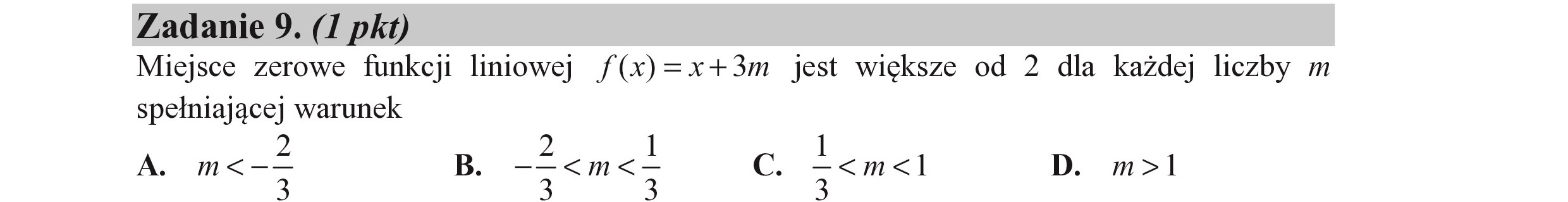
Zadanie 9. (I pkt) Miejsce zerowe funkcji liniowej /(x)=x+3m jest większe od 2 dla każdej liczby m spełniającej warunek A. PEL B. ama c. az! D. m>l ą ą ą ą


Zadanie 10. (I pkt) Na rysunku przedstawiony jest wykres funkcji f. k Wskaż wzór funkcji, której wykres jest symetryczny do wykresu funkcji f względem osi Oy układu współrzędnych. A. y=f(x—4) B. y=f(x)-4 c. y=f(x+4) D. y=f(x)+4

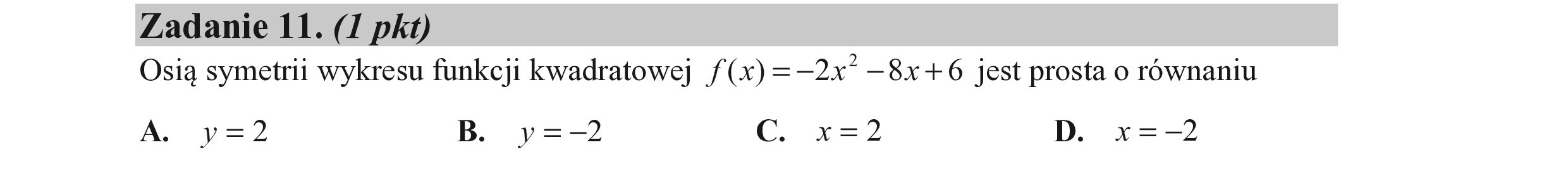
Zadanie 11. (I pkt) Osią symetrii wykresu funkcji kwadratowej f(x) =—2x* —8x+6 jest prosta o równaniu A. y=2 B. y=—2 C. x=2 D. x=—2


Zadanie 12. (I pkt) Ciąg (a,) jest określony dla n>l wzorem: a, =2n-1. Suma jedenastu początkowych wyrazów tego ciągu jest równa A. 101 B. 121 c, BB D. 81


Zadanie 13. (I pkt) Dany jest ciąg arytmetyczny (a,) dla n>l, w którym a,=1l oraz a,,=lll. Wtedy różnica r tego ciągu jest równa 9 10 — B. —100 la — D. 100 10 b


Zadanie 14. (I pkt) W trójkącie prostokątnym o długościach przyprostokątnych 2 i 5 cosinus większego z kątów ostrych jest równy A. * B. 8 2 5 D. z]e o z] o


Zadanie 15. (I pkt) Kąt a jest ostry oraz J3sina -43cosa=0. Wtedy A. tga=> B. tga=3 c. tga=N3 D. ga= 3


Zadanie 16. (I pkt) Dłuższa przekątna sześciokąta foremnego ma długość 24/2. Pole tego sześciokąta jest równe A. 1243 B. 643 C. 243 D. 343


Zadanie 17. (I pkt) Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku 1:4, mogą być równe A. 9136 B. 181 36 C. 9; 144 D. 18 1 144


Zadanie 18. (I pkt) Punkty 4=(3,2) i C są przeciwległymi wierzchołkami kwadratu ABCD, a punkt O = (6,5) jest środkiem okręgu opisanego na tym kwadracie. Współrzędne punktu C są równe A. (9,8) B. (15,12) c. [4933 D. (3,3)


Zadanie 19. (I pkt) Okrąg opisany równaniem (x-3) +(v+2) =r* jest styczny do osi Oy. Promień r tego okręgu jest równy A. WI3 B. 5 C. 3 D. 2


Zadanie 20. (I pkt) Każda krawędź ostrosłupa prawidłowego trójkątnego ma długość 9 (ostrosłup taki jest nazywany czworościanem foremnym). Wysokość tego ostrosłupa jest równa A. 346 B. 34/3 Cc. 206 D. 3/2


Zadanie 21. (I pkt) Dane są punkty A=(2,3) oraz B=(—6,—3). Promień okręgu wpisanego w trójkąt równoboczny ABC jest równy 593 1093 2093 p. 403 6, 53 h 3 3 3 3 A.


Zadanie 22. (I pkt) Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 36, a miara kąta nachylenia przekątnej graniastosłupa do płaszczyzny jego podstawy jest równa 307. Wysokość tego graniastosłupa jest równa A. 32 B. 642 Cc. 206 D. 346


Zadanie 23. (I pkt) Ze zbioru 40, 1, 2, ..., 15) losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe A. 2 ca B. 3 c Ć p. — 16 8 IE 13


Zadanie 24. (I pkt) Medianą zestawu danych 9, I, 4, x, 7,9 jest liczba 8. Wtedy x może być równe A. 8 B. 4 GTI D. 9


Zadanie 25. (I pkt) Ile jest wszystkich liczb czterocyfrowych, większych od 3000, utworzonych wyłącznie z cyfr l, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane? A. 3 B. 27 GC. 9 D. 6


Zadanie 26. (2 pkt) Rozwiąż równanie 8x +8x —3x-3=0.


Zadanie 27. (2 pkt) Rozwiąż nierówność 5x —45<0.


Zadanie 28. (2 pkt) Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 4 polegającego na tym, że otrzymamy liczbę podzielną przez 9 lub podzielną przez 12.

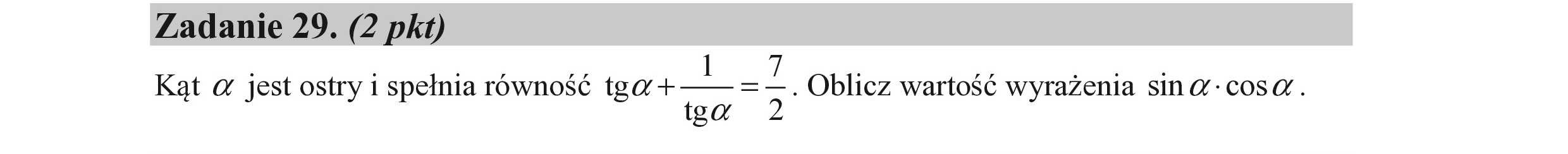
Zadanie 29. (2 pkt) | | o zy I 7 | r R. -8 Kąt a jest ostry 1 spełnia równość "= = 7 . Oblicz wartość wyrażenia sin: cosa. ga


Zadanie 30. (2 pkt) Udowodnij, że dla wszystkich nieujemnych liczb rzeczywistych x, vy prawdziwa jest nierówność x +y żxy+xy”.

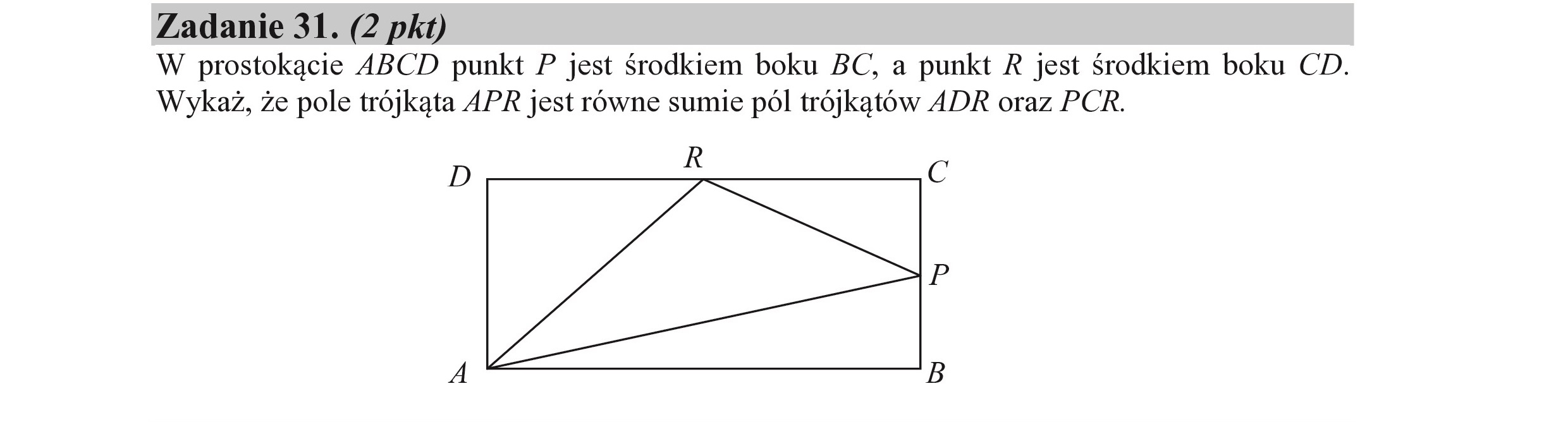
Zadanie 31. (2 pkt) W prostokącie ABCD punkt P jest środkiem boku BC, a punkt R jest środkiem boku CD. Wykaż, że pole trójkąta APR jest równe sumie pól trójkątów ADR oraz PCR. R Cc =], Zaih D


Zadanie 32. (4 pkt) Dany jest ciąg arytmetyczny (a,) o różnicy r +0 i pierwszym wyrazie a, =2. Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.


Zadanie 33. (4 pkt) Wyznacz równanie osi symetrii trójkąta o wierzchołkach 4=(—2,2), B=(6,—2), C=f(10,6).


Zadanie 34. (5 pkt) W ostrosłupie prawidłowym czworokątnym Ściana boczna o polu równym 10 jest nachylona do płaszczyzny podstawy pod kątem 60”. Oblicz objętość tego ostrosłupa.

MATEMATYKA 2015 SIERPIEN POPRAWKOWA STARA PODSTAWOWA

Zadanie 1. (I pkt) l : Ż . a+b Niech a= 3 b= zy Wtedy wartość wyrażenia ka A, B. 2 5 jest równa b |w


Zadanie 2. (I pkt) Cenę pewnego towaru obniżano dwukrotnie, za każdym razem o 20%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką A. 040%. B. o 36%. GC. 632%. D. o 28%.


Zadanie 3. (I pkt) 12 95 Liczba —— 150 jest równa A. 25 B. ą7 ą3 23 27


Zadanie 4. (I pkt) W rozwinięciu dziesiętnym ułamka = na trzydziestym miejscu po przecinku stoi cyfra A. 7 B. I G 2 D. 4


Zadanie 5. (I pkt) Wskaż największą liczbę całkowitą spełniającą nierówność 47 3<0. A. 5 B. 6 Cc. 7 D. 8

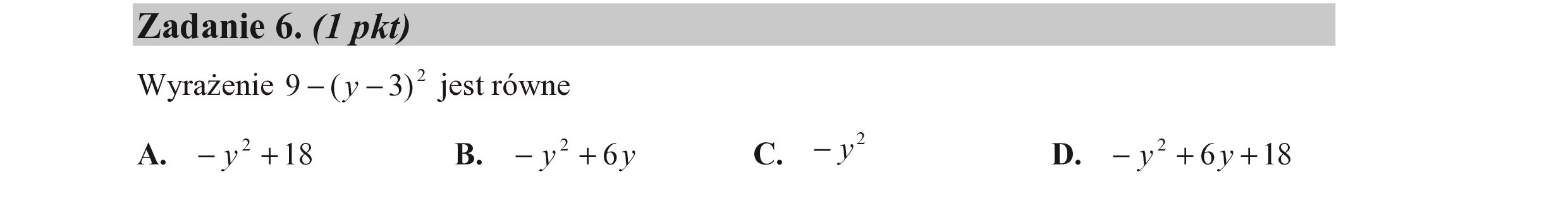
Zadanie 6. (I pkt) Wyrażenie 9 — (y —3)” jest równe J A. —y*+18 B. -y'+ó6y c. "FP D. -y'+6y+18


Zadanie 7. (I pkt) = R 1 25... Iloczyn liczb spełniających równanie kg 4 =() jest równy A. 6 B. —5 LC. 5


Zadanie 8. (I pkt) Wierzchołek paraboli będącej wykresem funkcji kwadratowej y = f(x) ma współrzędne (2,2). Wówczas wierzchołek paraboli będącej wykresem funkcji g(x)=/(x+2) ma współrzędne A. (0,2) B. (4,2) c. (2,0) D. (2,4)

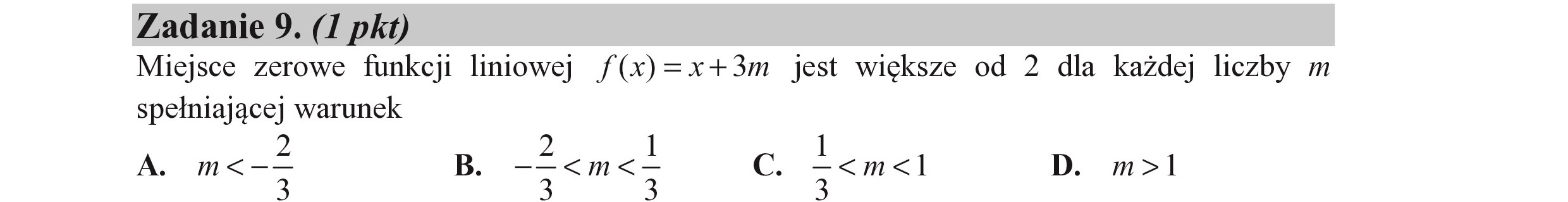
Zadanie 9. (I pkt) Miejsce zerowe funkcji liniowej /(x)=x+3m jest większe od 2 dla każdej liczby m spełniającej warunek A. PEL B. ama c. az! D. m>l ą ą ą ą


Zadanie 10. (I pkt) Na rysunku przedstawiony jest wykres funkcji f. k Wskaż wzór funkcji, której wykres jest symetryczny do wykresu funkcji f względem osi Oy układu współrzędnych. A. y=f(x—4) B. y=f(x)-4 c. y=f(x+4) D. y=f(x)+4

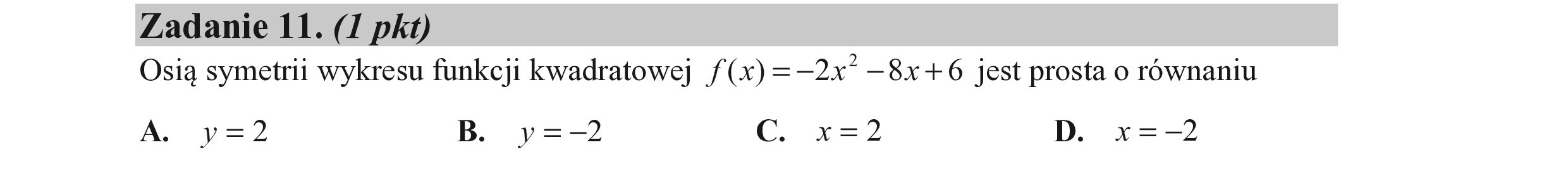
Zadanie 11. (I pkt) Osią symetrii wykresu funkcji kwadratowej f(x) =—2x* —8x+6 jest prosta o równaniu A. y=2 B. y=—2 C. x=2 D. x=—2


Zadanie 12. (I pkt) Ciąg (a,) jest określony dla n>l wzorem: a, =2n-1. Suma jedenastu początkowych wyrazów tego ciągu jest równa A. 101 B. 121 c, BB D. 81


Zadanie 13. (I pkt) Dany jest ciąg arytmetyczny (a,) dla n>l, w którym a,=1l oraz a,,=lll. Wtedy różnica r tego ciągu jest równa 9 10 — B. —100 la — D. 100 10 b


Zadanie 14. (I pkt) W trójkącie prostokątnym o długościach przyprostokątnych 2 i 5 cosinus większego z kątów ostrych jest równy A. * B. 8 2 5 D. z]e o z] o


Zadanie 15. (I pkt) Kąt a jest ostry oraz J3sina -43cosa=0. Wtedy A. tga=> B. tga=3 c. tga=N3 D. ga= 3


Zadanie 16. (I pkt) Dłuższa przekątna sześciokąta foremnego ma długość 24/2. Pole tego sześciokąta jest równe A. 1243 B. 643 C. 243 D. 343


Zadanie 17. (I pkt) Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku 1:4, mogą być równe A. 9136 B. 181 36 C. 9; 144 D. 18 1 144


Zadanie 18. (I pkt) Punkty 4=(3,2) i C są przeciwległymi wierzchołkami kwadratu ABCD, a punkt O = (6,5) jest środkiem okręgu opisanego na tym kwadracie. Współrzędne punktu C są równe A. (9,8) B. (15,12) c. [4933 D. (3,3)


Zadanie 19. (I pkt) Okrąg opisany równaniem (x-3) +(v+2) =r* jest styczny do osi Oy. Promień r tego okręgu jest równy A. WI3 B. 5 C. 3 D. 2


Zadanie 20. (I pkt) Każda krawędź ostrosłupa prawidłowego trójkątnego ma długość 9 (ostrosłup taki jest nazywany czworościanem foremnym). Wysokość tego ostrosłupa jest równa A. 346 B. 34/3 Cc. 206 D. 3/2


Zadanie 21. (I pkt) Dane są punkty A=(2,3) oraz B=(—6,—3). Promień okręgu wpisanego w trójkąt równoboczny ABC jest równy 593 1093 2093 p. 403 6, 53 h 3 3 3 3 A.


Zadanie 22. (I pkt) Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 36, a miara kąta nachylenia przekątnej graniastosłupa do płaszczyzny jego podstawy jest równa 307. Wysokość tego graniastosłupa jest równa A. 32 B. 642 Cc. 206 D. 346


Zadanie 23. (I pkt) Ze zbioru 40, 1, 2, ..., 15) losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe A. 2 ca B. 3 c Ć p. — 16 8 IE 13


Zadanie 24. (I pkt) Medianą zestawu danych 9, I, 4, x, 7,9 jest liczba 8. Wtedy x może być równe A. 8 B. 4 GTI D. 9


Zadanie 25. (I pkt) Ile jest wszystkich liczb czterocyfrowych, większych od 3000, utworzonych wyłącznie z cyfr l, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane? A. 3 B. 27 GC. 9 D. 6


Zadanie 26. (2 pkt) Rozwiąż równanie 8x +8x —3x-3=0.


Zadanie 27. (2 pkt) Rozwiąż nierówność 5x —45<0.


Zadanie 28. (2 pkt) Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 4 polegającego na tym, że otrzymamy liczbę podzielną przez 9 lub podzielną przez 12.

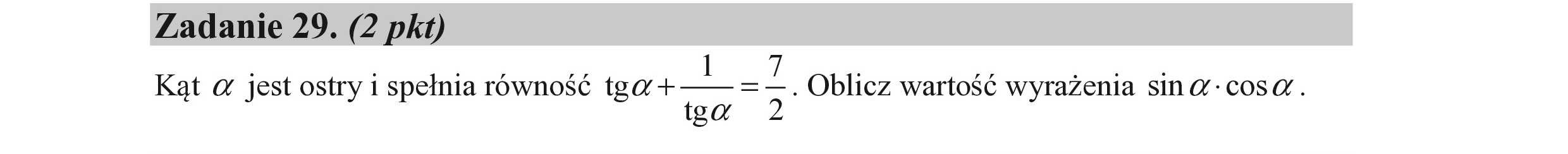
Zadanie 29. (2 pkt) | | o zy I 7 | r R. -8 Kąt a jest ostry 1 spełnia równość "= = 7 . Oblicz wartość wyrażenia sin: cosa. ga


Zadanie 30. (2 pkt) Udowodnij, że dla wszystkich nieujemnych liczb rzeczywistych x, vy prawdziwa jest nierówność x +y żxy+xy”.


Zadanie 31. (2 pkt) W prostokącie ABCD punkt P jest środkiem boku BC, a punkt R jest środkiem boku CD. Wykaż, że pole trójkąta APR jest równe sumie pól trójkątów ADR oraz PCR. R Cc =], Zaih D


Zadanie 32. (4 pkt) Dany jest ciąg arytmetyczny (a,) o różnicy r +0 i pierwszym wyrazie a, =2. Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.


Zadanie 33. (4 pkt) Wyznacz równanie osi symetrii trójkąta o wierzchołkach 4=(—2,2), B=(6,—2), C=f(10,6).


Zadanie 34. (5 pkt) W ostrosłupie prawidłowym czworokątnym Ściana boczna o polu równym 10 jest nachylona do płaszczyzny podstawy pod kątem 60”. Oblicz objętość tego ostrosłupa.






























