MATEMATYKA 2015 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) A. Ż B. 1 3 . 3, "= -b Jeśli a =— i b=2, to wartość wyrażenia ka ż. a+ jest równa b c. 7


Zadanie 2. (0—1) Dany jest prostokąt o wymiarach 40cm x 100cm. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta A. zwiększy się o 8%. B. zwiększy się o 4%. C. zmniejszy się o 8%. D zmniejszy się o 4%.


Zadanie 3. (0—1) Liczba A. 45” 5 45 9 jest równa B. 45 9 54


Zadanie 4. (0—1) ; 9 4, , Liczba Ę + E jest równa 7 9 A. Ę 6 p. C. 1 D. 3+N7 63 3/7 3/7


Zadanie 5. (0—1) . 1 . Wartość wyrażenia log, O, 05» 5.log,, 1 jest równa A. -3 B. 24 GC -2

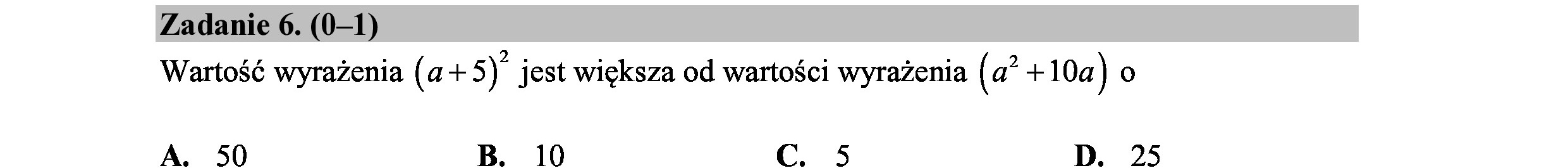
Zadanie 6. (0—1) Wartość wyrażenia (a+ 5) jest większa od wartości wyrażenia (a? + 10a) o A. 50 B. 10 C. 5 D. 25

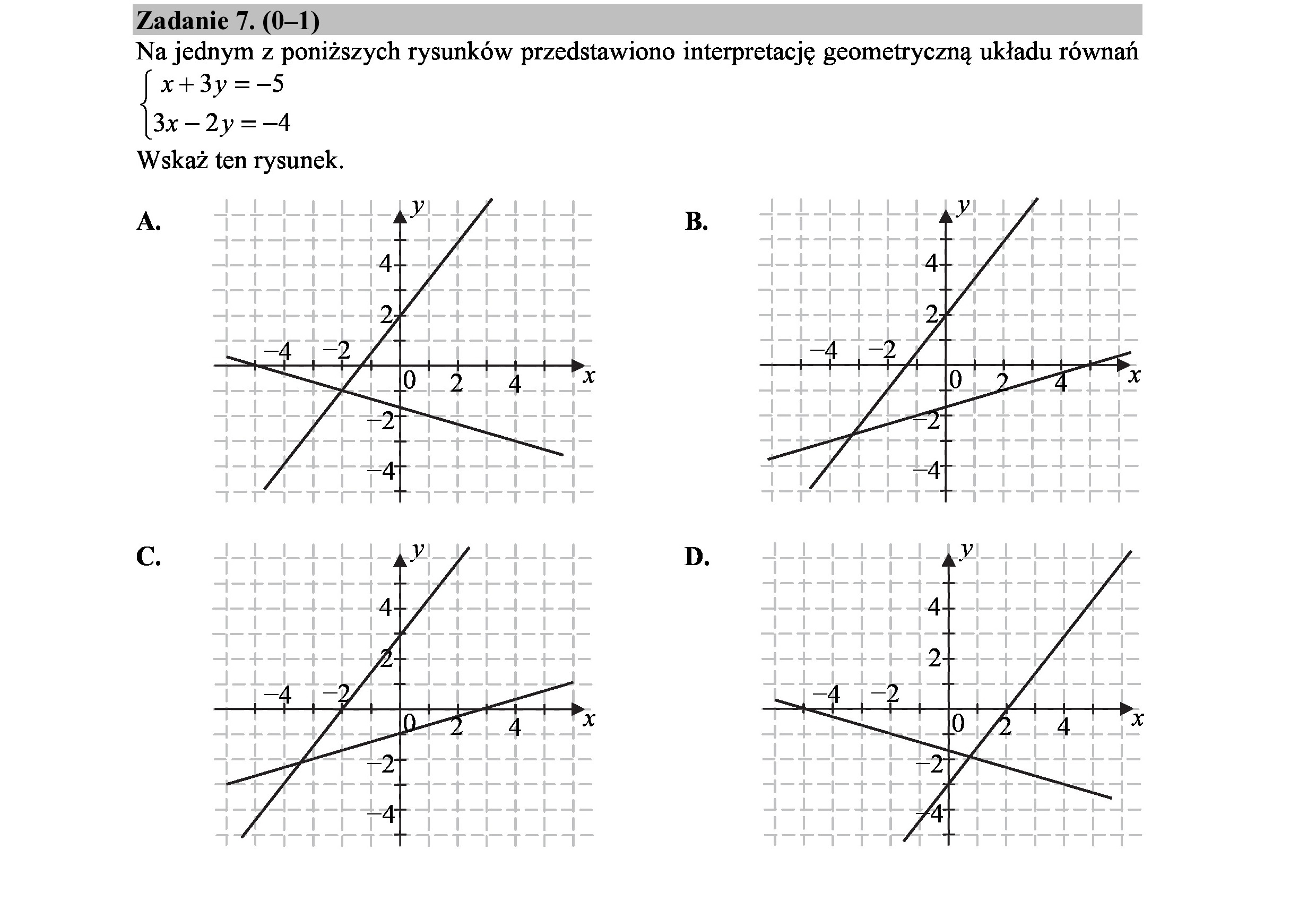
Zadanie 7. (0—1) Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań x+3y=—5 b —2y=-4 Wskaż ten rysunek. A.


Zadanie 8. (0—1) Najmniejszą liczbą całkowitą spełniającą nierówność 2(x —2)<4(x—1)+1 jest A. -2 B. -1 c. 0 D. I


Zadanie 9. (0—1) Rozwiązaniem równania x (x +1)= x” —8 jest A. -9 B. -2 c. 2


Zadanie 10. (0—1) y= Funkcja f jest określona wzorem f(x)= sd x dla każdej liczby rzeczywistej x=0. Wówczas wartość funkcji f (4/2 ) jest równa A. 2-442 B. 1-242 C. 1+242 D. 2+44/2


Zadanie 11. (0—1) Parabola o wierzchołku W =(-3,5) i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem A. y=2-(x+3) +5 B. y=-2-(x-3) +5 C. y=—2-(x+3) +5 D. y=—2-(x—3) -5

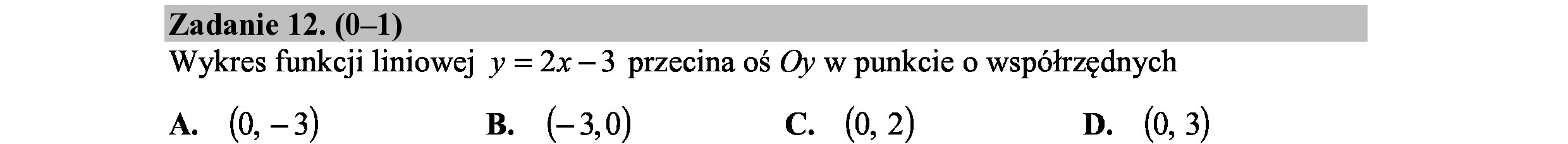
Zadanie 12. (0—1) Wykres funkcji liniowej y = 2x—3 przecina oś Oy w punkcie o współrzędnych A. (0, -3) B. (-3,0) c. (0, 2) D. (0,3)


Zadanie 13. (0—1) Wierzchołek paraboli będącej wykresem funkcji kwadratowej y = f(x) ma współrzędne (2,2). Wówczas wierzchołek paraboli będącej wykresem funkcji g(x)=/f(x+2) ma współrzędne A. (4,2) B. (0,2) c. (2,0) D. (2,4)


Zadanie 14. (0—1) Wszystkie dwucyfrowe liczby naturalne podzielne przez 7 tworzą rosnący ciąg arytmetyczny. Dwunastym wyrazem tego ciągu jest liczba A. 77 B. 84 C. 91 D. 98

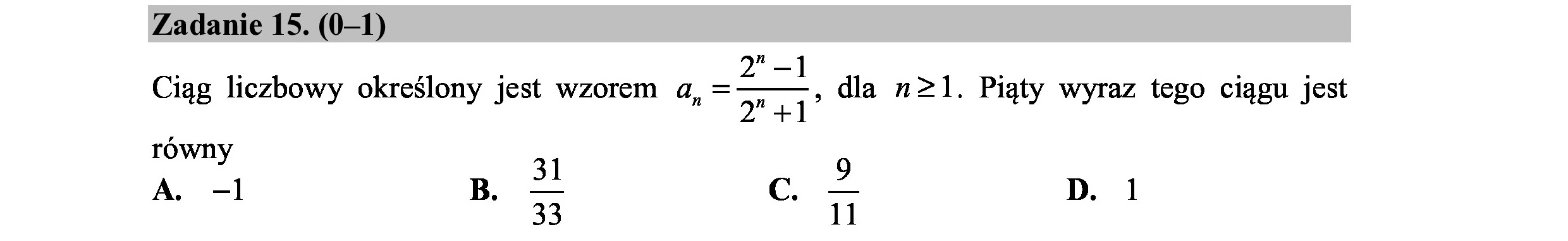
Zadanie 15. (0—1) Ciąg liczbowy określony jest wzorem a, = r" h dla n>1. Piąty wyraz tego ciągu jest równy 31 ) D. 1 A. -1 srt Cc 33 11


Zadanie 16. (0—1) : NE ŚP wdić Sinus kąta ostrego a jest równy 4 „ Wówczas A. —— B. asap t”. c. LI D. azyapo 4 4 16 16


Zadanie 17. (0—1) W trójkącie prostokątnym o długościach przyprostokątnych 2 1 5 cosinus większego z kątów ostrych jest równy 5 2 p. | A. — B. — Cc — D. 2 sj N29 N29


Zadanie 18. (0—1) Pole rombu o boku 6 i kącie rozwartym 150? jest równe A. 1842 B. 18 c. 36/2 D. 36

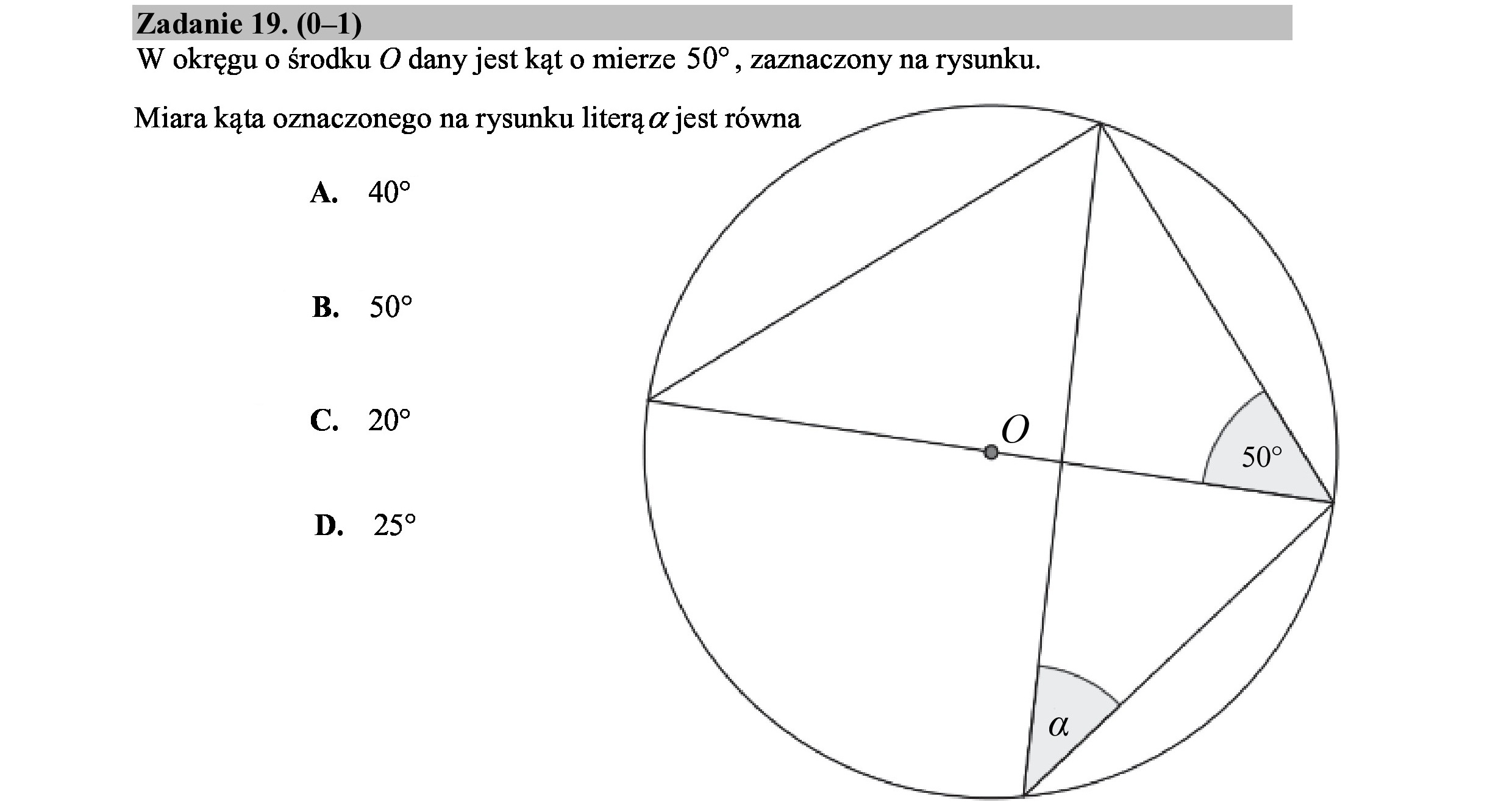
Zadanie 19. (0—1) W okręgu o środku O dany jest kąt o mierze 50”, zaznaczony na rysunku. Miara kąta oznaczonego na rysunku literą a jest równa A. 40 B. 50? c. 20? D. 259

Zadanie 20. (0—1) Współczynnik kierunkowy prostej, na której leżą punkty 4=(—4,3) oraz B=(8,7), jest równy A. a=3 B. a=—1 c. a=> D. a=

Zadanie 21. (0—1) Punkt S=(2,—5) jest środkiem odcinka 4B, gdzie 4 =(—4,3) i B=(8,b). Wtedy A. b=—13 B. b=—2 C. b=-1 D. b=6


Zadanie 22. (0—1)
Dany jest trójkąt prostokątny o długościach boków a, b, c, gdzie a

Zadanie 23. (0—1) Przekątna przekroju osiowego walca, którego promień podstawy jest równy 4 i wysokość jest równa 6, ma długość A. AM10 B. 420 c. 452 D. 10


Zadanie 24. (0—1) W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że będzie to kobieta, jest równe p. 5 A, — B. — 5 : 15 33 33 18


Zadanie 25. (0—1) Ile jest wszystkich liczb czterocyfrowych, większych od 3000, utworzonych wyłącznie z cyfr 1, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane? A. 3 B. 6 c. 9 D. 27

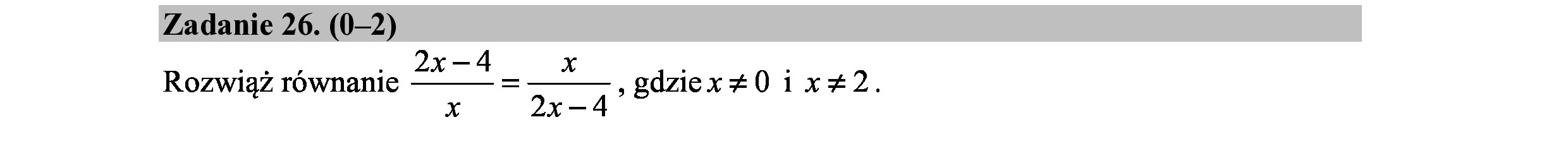
Zadanie 26. (0—2) NT . 2x— x : * Rozwiąż równanie = „gdziexe0ix*2. x 2x—4


Zadanie 27. (0-2) Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim — 8 kul ponumerowanych kolejnymi liczbami od 1 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego — cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 11.


Zadanie 28. (0—2) Rozwiąż nierówność 20x > 4x” +24.

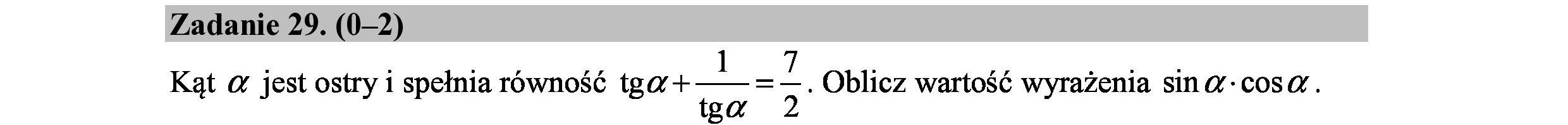
Zadanie 29. (0—2) : : =" az 1 7 ! r SESE Kąt a jest ostry 1 spełnia równość i dur== s z: Oblicz wartość wyrażenia sin: cos. ga


Zadanie 30. (0—2) Wykaż, że dla wszystkich nieujemnych liczb rzeczywistych x, y prawdziwa jest nierówność x ły żxy+xy.

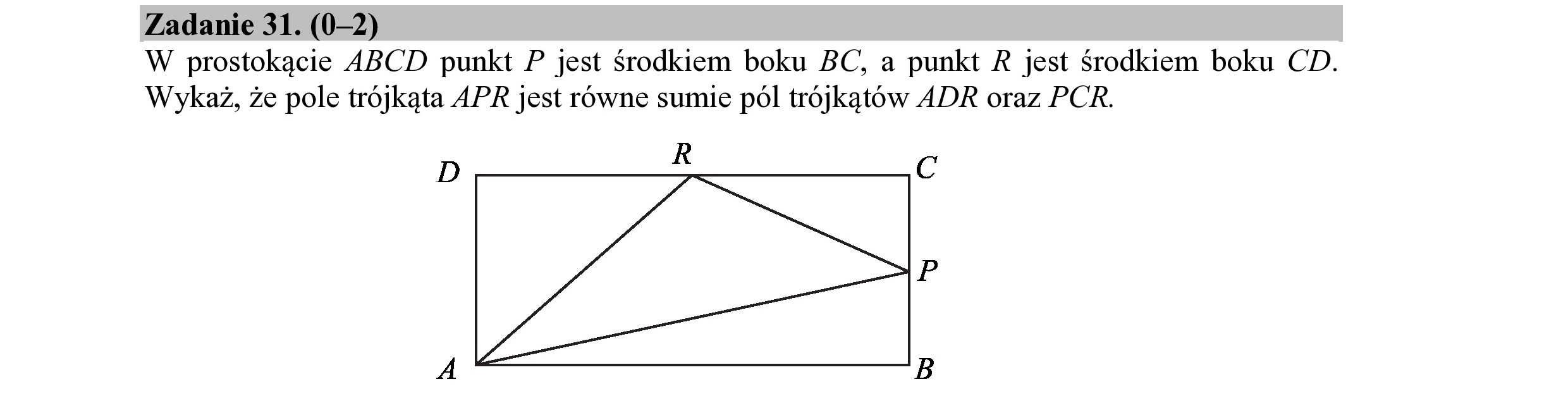
Zadanie 31. (0—2) W prostokącie ABCD punkt P jest środkiem boku BC, a punkt R jest środkiem boku CD. Wykaż, że pole trójkąta APR jest równe sumie pól trójkątów ADR oraz PCR. D R Cc =] fo


Zadanie 32. (0—4) Wyznacz równanie osi symetrii trójkąta o wierzchołkach 4=(—2,2), B=(6,—2), C=(10,6).

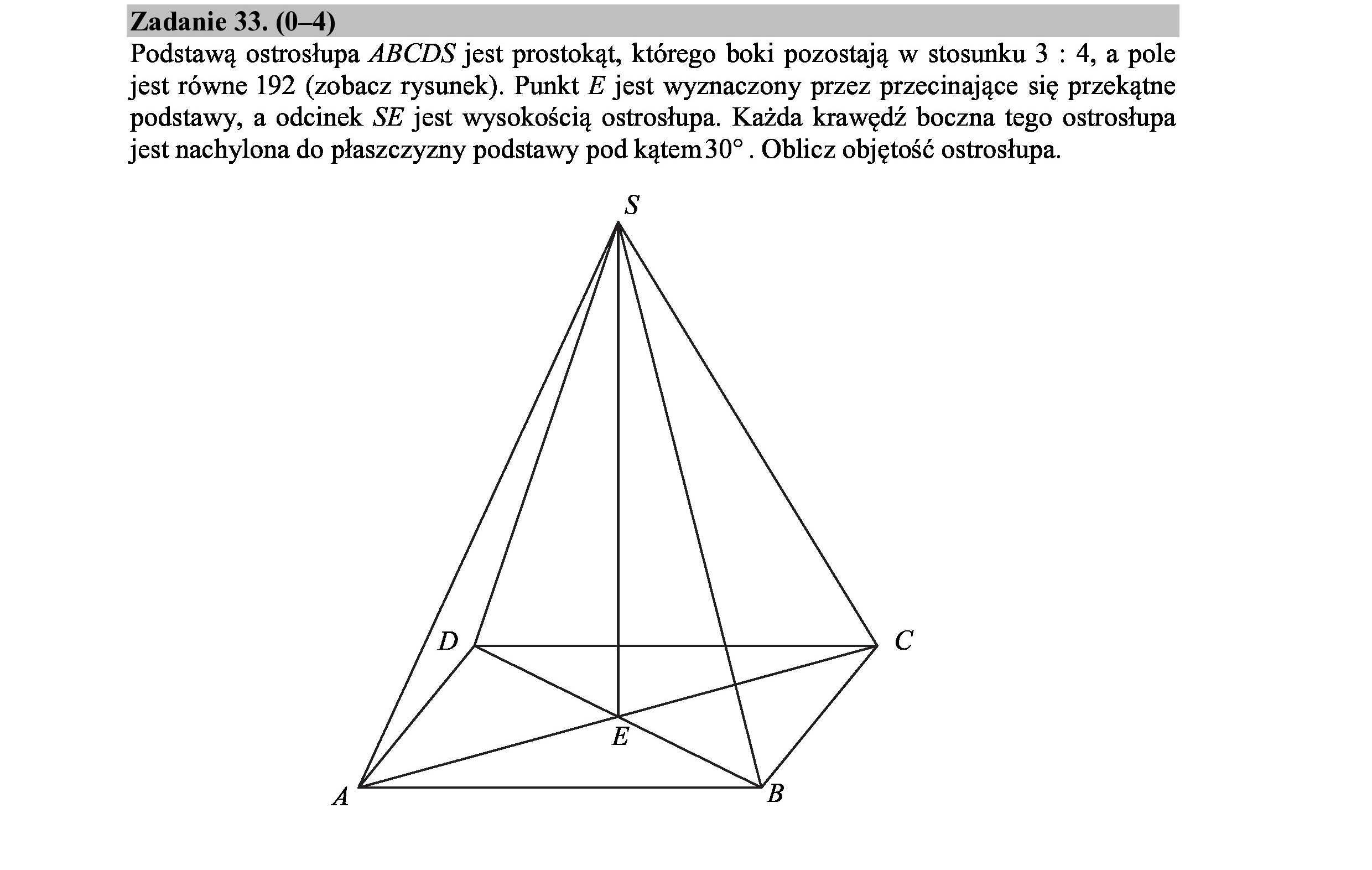
Zadanie 33. (0—4) Podstawą ostrosłupa ABCDS jest prostokąt, którego boki pozostają w stosunku 3 : 4, a pole jest równe 192 (zobacz rysunek). Punkt £ jest wyznaczony przez przecinające się przekątne podstawy, a odcinek SE jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 30? . Oblicz objętość ostrosłupa. S (>< A


Zadanie 34. (0—5) Funkcja kwadratowa f określona jest wzorem f(x)=ax* +bx+c. Zbiorem rozwiązań nierówności f(x)> 0 jest przedział (0,12). Największa wartość funkcji f jest równa 9. Oblicz współczynniki a, b i c funkcji f.

MATEMATYKA 2015 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (0—1) A. Ż B. 1 3 . 3, "= -b Jeśli a =— i b=2, to wartość wyrażenia ka ż. a+ jest równa b c. 7


Zadanie 2. (0—1) Dany jest prostokąt o wymiarach 40cm x 100cm. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta A. zwiększy się o 8%. B. zwiększy się o 4%. C. zmniejszy się o 8%. D zmniejszy się o 4%.


Zadanie 3. (0—1) Liczba A. 45” 5 45 9 jest równa B. 45 9 54


Zadanie 4. (0—1) ; 9 4, , Liczba Ę + E jest równa 7 9 A. Ę 6 p. C. 1 D. 3+N7 63 3/7 3/7


Zadanie 5. (0—1) . 1 . Wartość wyrażenia log, O, 05» 5.log,, 1 jest równa A. -3 B. 24 GC -2

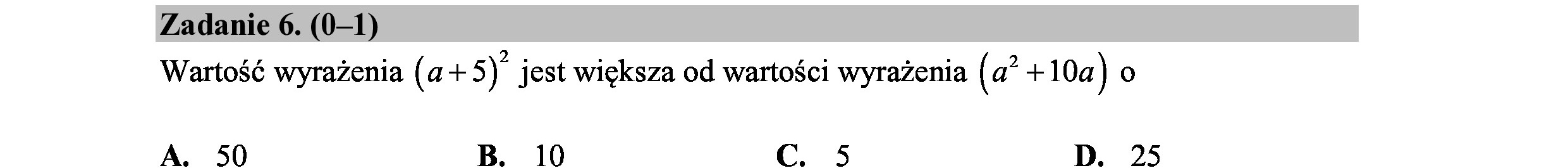
Zadanie 6. (0—1) Wartość wyrażenia (a+ 5) jest większa od wartości wyrażenia (a? + 10a) o A. 50 B. 10 C. 5 D. 25


Zadanie 7. (0—1) Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań x+3y=—5 b —2y=-4 Wskaż ten rysunek. A.


Zadanie 8. (0—1) Najmniejszą liczbą całkowitą spełniającą nierówność 2(x —2)<4(x—1)+1 jest A. -2 B. -1 c. 0 D. I


Zadanie 9. (0—1) Rozwiązaniem równania x (x +1)= x” —8 jest A. -9 B. -2 c. 2


Zadanie 10. (0—1) y= Funkcja f jest określona wzorem f(x)= sd x dla każdej liczby rzeczywistej x=0. Wówczas wartość funkcji f (4/2 ) jest równa A. 2-442 B. 1-242 C. 1+242 D. 2+44/2


Zadanie 11. (0—1) Parabola o wierzchołku W =(-3,5) i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem A. y=2-(x+3) +5 B. y=-2-(x-3) +5 C. y=—2-(x+3) +5 D. y=—2-(x—3) -5

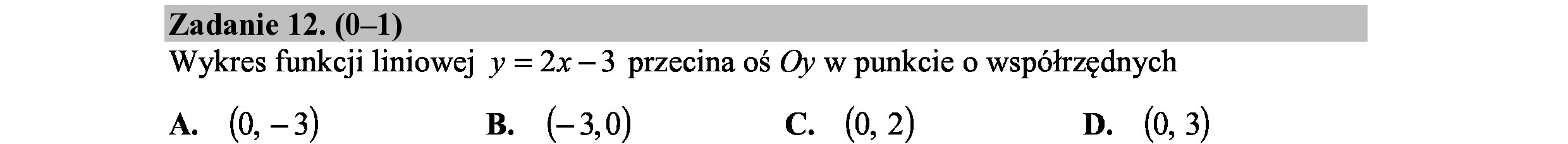
Zadanie 12. (0—1) Wykres funkcji liniowej y = 2x—3 przecina oś Oy w punkcie o współrzędnych A. (0, -3) B. (-3,0) c. (0, 2) D. (0,3)


Zadanie 13. (0—1) Wierzchołek paraboli będącej wykresem funkcji kwadratowej y = f(x) ma współrzędne (2,2). Wówczas wierzchołek paraboli będącej wykresem funkcji g(x)=/f(x+2) ma współrzędne A. (4,2) B. (0,2) c. (2,0) D. (2,4)


Zadanie 14. (0—1) Wszystkie dwucyfrowe liczby naturalne podzielne przez 7 tworzą rosnący ciąg arytmetyczny. Dwunastym wyrazem tego ciągu jest liczba A. 77 B. 84 C. 91 D. 98

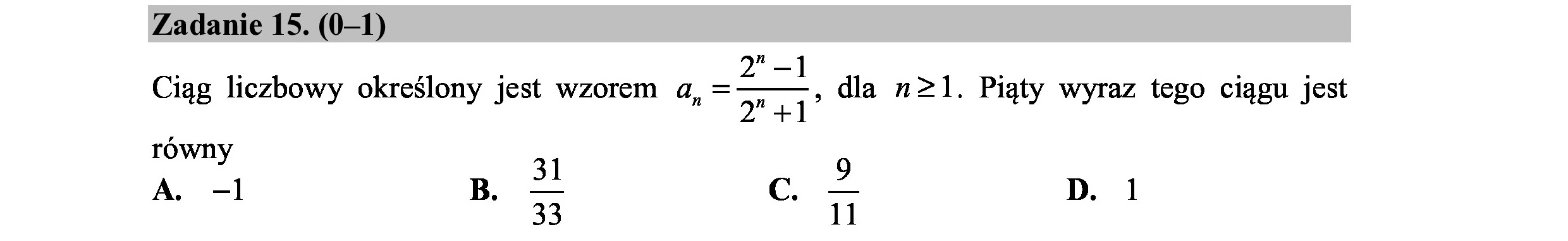
Zadanie 15. (0—1) Ciąg liczbowy określony jest wzorem a, = r" h dla n>1. Piąty wyraz tego ciągu jest równy 31 ) D. 1 A. -1 srt Cc 33 11


Zadanie 16. (0—1) : NE ŚP wdić Sinus kąta ostrego a jest równy 4 „ Wówczas A. —— B. asap t”. c. LI D. azyapo 4 4 16 16


Zadanie 17. (0—1) W trójkącie prostokątnym o długościach przyprostokątnych 2 1 5 cosinus większego z kątów ostrych jest równy 5 2 p. | A. — B. — Cc — D. 2 sj N29 N29


Zadanie 18. (0—1) Pole rombu o boku 6 i kącie rozwartym 150? jest równe A. 1842 B. 18 c. 36/2 D. 36


Zadanie 19. (0—1) W okręgu o środku O dany jest kąt o mierze 50”, zaznaczony na rysunku. Miara kąta oznaczonego na rysunku literą a jest równa A. 40 B. 50? c. 20? D. 259

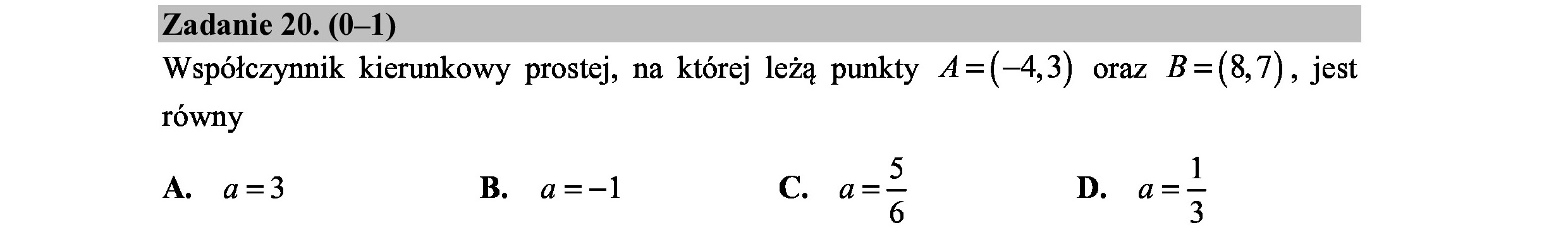
Zadanie 20. (0—1) Współczynnik kierunkowy prostej, na której leżą punkty 4=(—4,3) oraz B=(8,7), jest równy A. a=3 B. a=—1 c. a=> D. a=

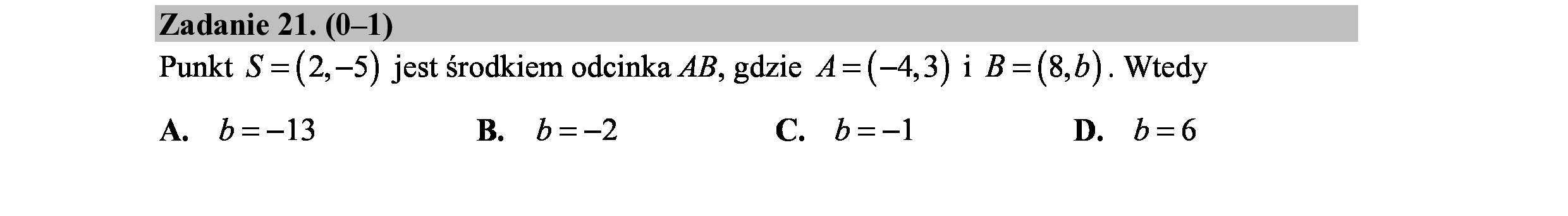
Zadanie 21. (0—1) Punkt S=(2,—5) jest środkiem odcinka 4B, gdzie 4 =(—4,3) i B=(8,b). Wtedy A. b=—13 B. b=—2 C. b=-1 D. b=6


Zadanie 22. (0—1) Dany jest trójkąt prostokątny o długościach boków a, b, c, gdzie a<b<c. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 3609, otrzymujemy bryłę, której objętość jest równa A. VF= zaw B. V=aba Cc VF= zb'am D. F=aa+zac


Zadanie 23. (0—1) Przekątna przekroju osiowego walca, którego promień podstawy jest równy 4 i wysokość jest równa 6, ma długość A. AM10 B. 420 c. 452 D. 10


Zadanie 24. (0—1) W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że będzie to kobieta, jest równe p. 5 A, — B. — 5 : 15 33 33 18


Zadanie 25. (0—1) Ile jest wszystkich liczb czterocyfrowych, większych od 3000, utworzonych wyłącznie z cyfr 1, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane? A. 3 B. 6 c. 9 D. 27

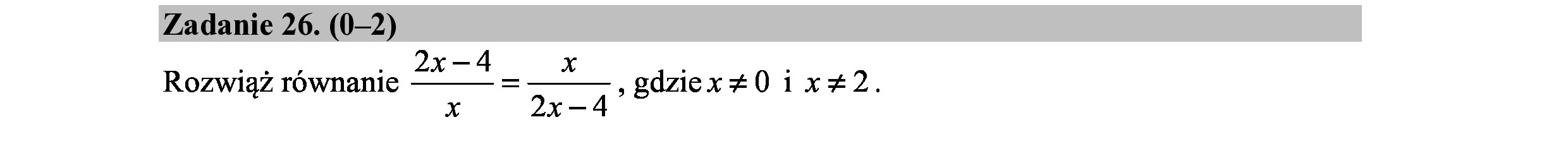
Zadanie 26. (0—2) NT . 2x— x : * Rozwiąż równanie = „gdziexe0ix*2. x 2x—4


Zadanie 27. (0-2) Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim — 8 kul ponumerowanych kolejnymi liczbami od 1 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego — cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 11.


Zadanie 28. (0—2) Rozwiąż nierówność 20x > 4x” +24.

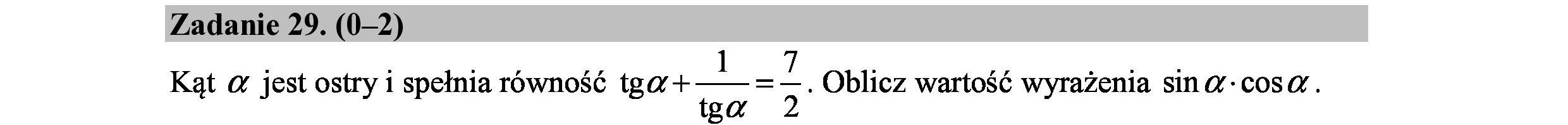
Zadanie 29. (0—2) : : =" az 1 7 ! r SESE Kąt a jest ostry 1 spełnia równość i dur== s z: Oblicz wartość wyrażenia sin: cos. ga


Zadanie 30. (0—2) Wykaż, że dla wszystkich nieujemnych liczb rzeczywistych x, y prawdziwa jest nierówność x ły żxy+xy.


Zadanie 31. (0—2) W prostokącie ABCD punkt P jest środkiem boku BC, a punkt R jest środkiem boku CD. Wykaż, że pole trójkąta APR jest równe sumie pól trójkątów ADR oraz PCR. D R Cc =] fo


Zadanie 32. (0—4) Wyznacz równanie osi symetrii trójkąta o wierzchołkach 4=(—2,2), B=(6,—2), C=(10,6).


Zadanie 33. (0—4) Podstawą ostrosłupa ABCDS jest prostokąt, którego boki pozostają w stosunku 3 : 4, a pole jest równe 192 (zobacz rysunek). Punkt £ jest wyznaczony przez przecinające się przekątne podstawy, a odcinek SE jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 30? . Oblicz objętość ostrosłupa. S (>< A


Zadanie 34. (0—5) Funkcja kwadratowa f określona jest wzorem f(x)=ax* +bx+c. Zbiorem rozwiązań nierówności f(x)> 0 jest przedział (0,12). Największa wartość funkcji f jest równa 9. Oblicz współczynniki a, b i c funkcji f.






























