MATEMATYKA 2015 MAJ MATURA STARA PODSTAWOWA

Zadanie 1. (I pkt) Cena pewnego towaru wraz z 7-procentowym podatkiem VAT jest równa 34 347 zł. Cena tego samego towaru wraz z 23-procentowym podatkiem VAT będzie równa A. 37236 zł B. 39842,52 zł C. 39483 zł D. 42 246,81 zł


Zadanie 2. (I pkt) Najmniejszą liczbą całkowitą dodatnią spełniającą nierówność |r+ 4,5 26 jest A. x=l B. x=2 C. 5=3 D. x=6


4 Liczba 23 -V2' jest równa A. 23 B. 2 GG 2 D. 2


Zadanie 4. (I pkt) Liczba 2logz 10— logs; 4 jest równa A. 2 B. logs 96 Cc. 2logs6

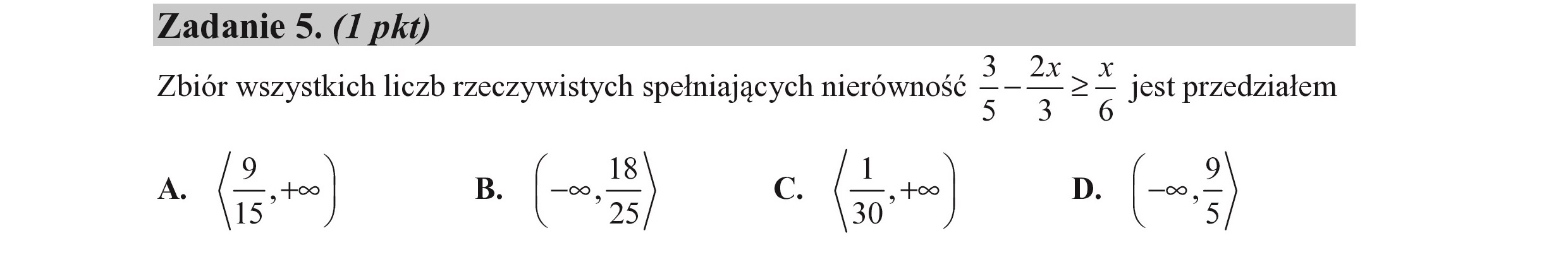
Zadanie 5. (I pkt) Zbiór wszystkich liczb rzeczywistych spełniających nierówność = = 2 5 jest przedziałem A. zo) B. [035 zę) D. ->5 15 23 30 3


Zadanie 6. (I pkt) Bieda hko f deoc wzi flej= 2 Xx — może być zbiór A. wszystkich liczb rzeczywistych różnych od 0 1 od 4. B. wszystkich liczb rzeczywistych różnych od —4 1 od 4. C. wszystkich liczb rzeczywistych różnych od —4 1 od 0. D. wszystkich liczb rzeczywistych.


Zadanie 7. (I pkt) Rozwiązaniem równania A. x=0 4 jest liczba


Zadanie 8. (I pkt) Miejscem zerowym funkcji liniowej określonej wzorem f(x) = —g* +4 jest A. 0 B. 6 C. 4 D. —6


Zadanie 9. (I pkt) l 2" A— : Punkt M -(3: ; należy do wykresu funkcji liniowej określonej wzorem J(3)=(3—2a)x+2. Wtedy A. gp" B. a=2 C. a= 1 D. a= p. 2

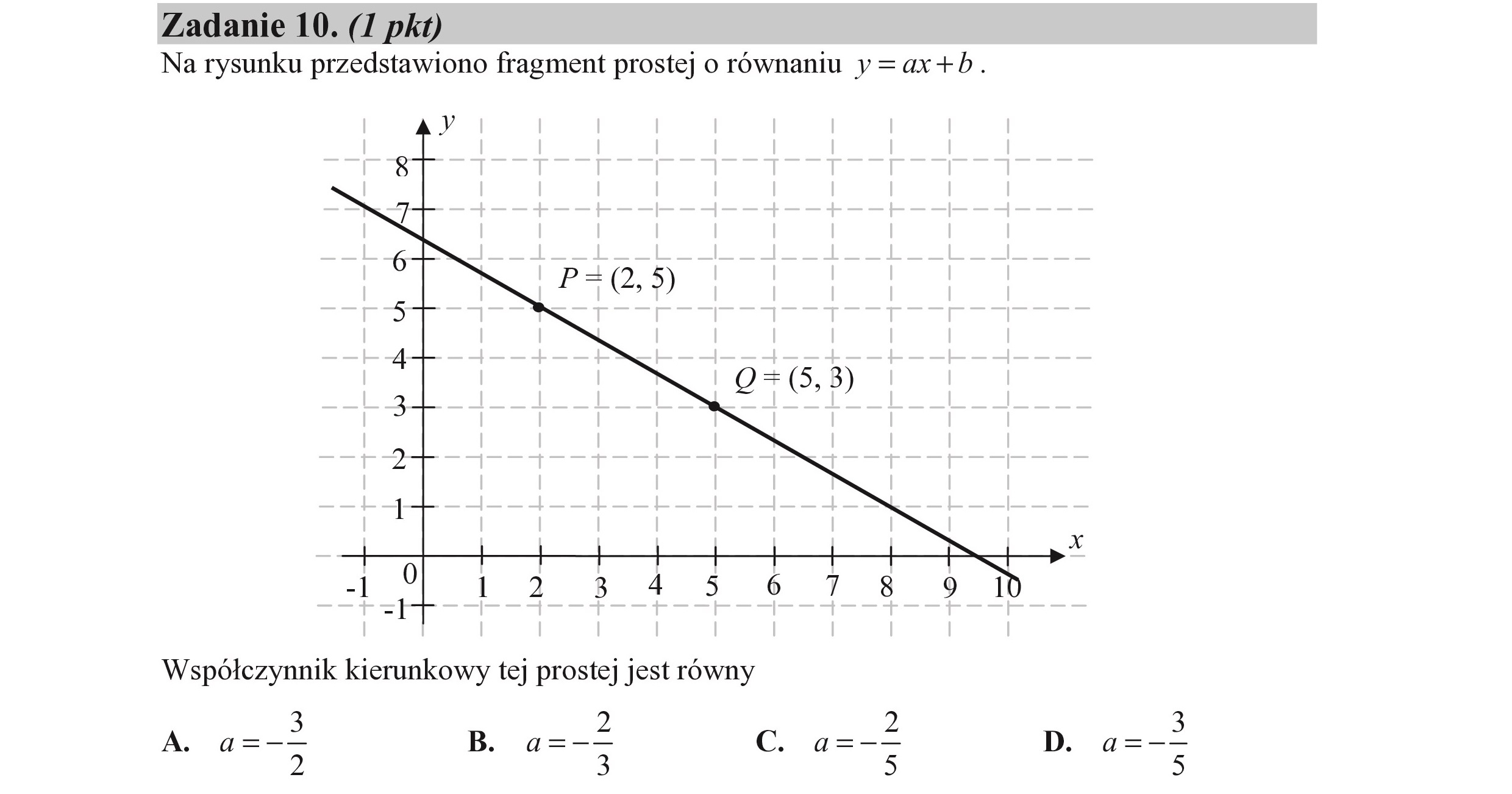
Zadanie 10. (I pkt) Na rysunku przedstawiono fragment prostej o równaniu y=ax+b. V = b» w© RE u O MAI %


Zadanie 11. (I pkt) W ciągu arytmetycznym (a) określonym dla n>1 dane są a, =-—4 i r=2. Którym wyrazem tego ciągu jest liczba 156? A. 81. B. 60. C. 76. D. 77.

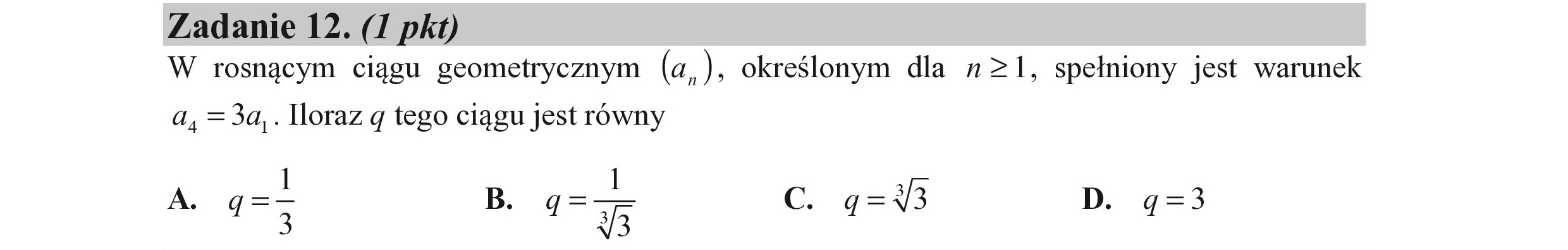
Zadanie 12. (I pkt) W rosnącym ciągu geometrycznym (a,), określonym dla n>1, spełniony jest warunek a, =3a,. lloraz q tego ciągu jest równy A. q=— B. q= C. q=3 D. q=3 3 5|-

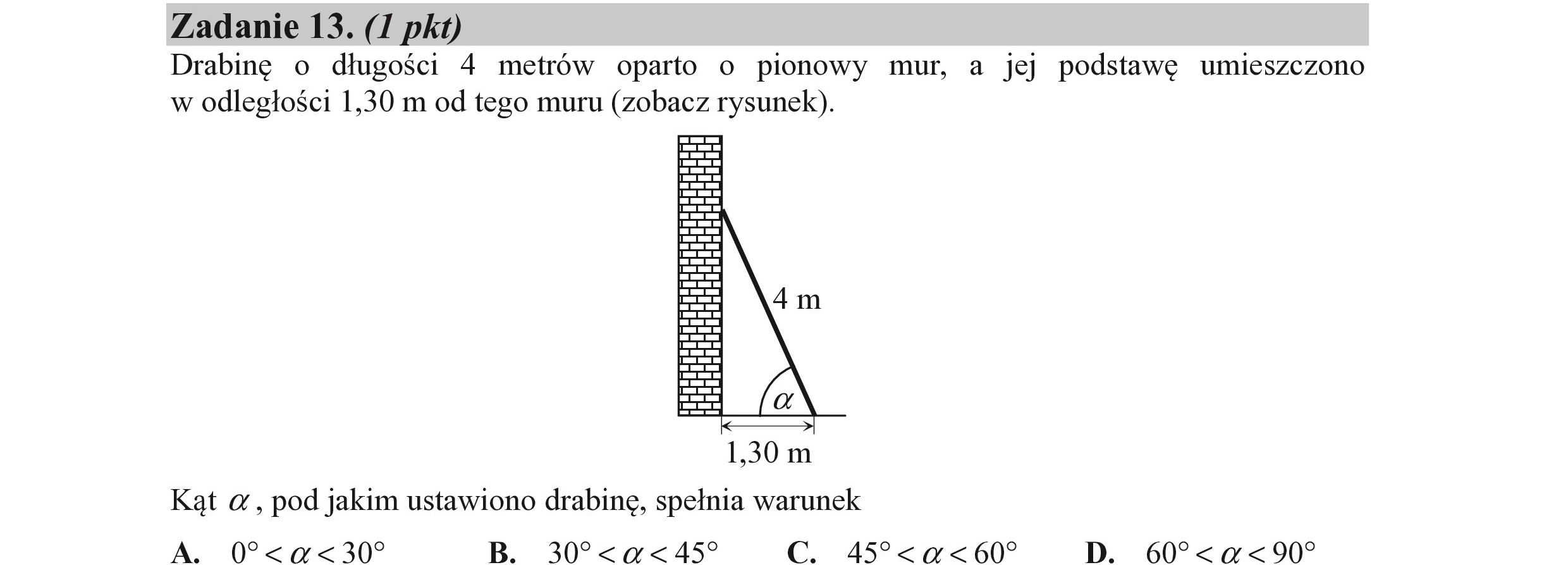
Zadanie 13. (I pkt)
Drabinę o długości 4 metrów oparto o pionowy mur, a jej podstawę umieszczono
w odległości 1,30 m od tego muru (zobacz rysunek).
1,30m
Kąt ©, pod jakim ustawiono drabinę, spełnia warunek
A. 0O

Zadanie 14. (I pkt) . |. 2 , . ż Kąt a jest ostry 1 sina = rh Wówczas cos a jest równy A. p. JE 5 3 2 4 u|5] —

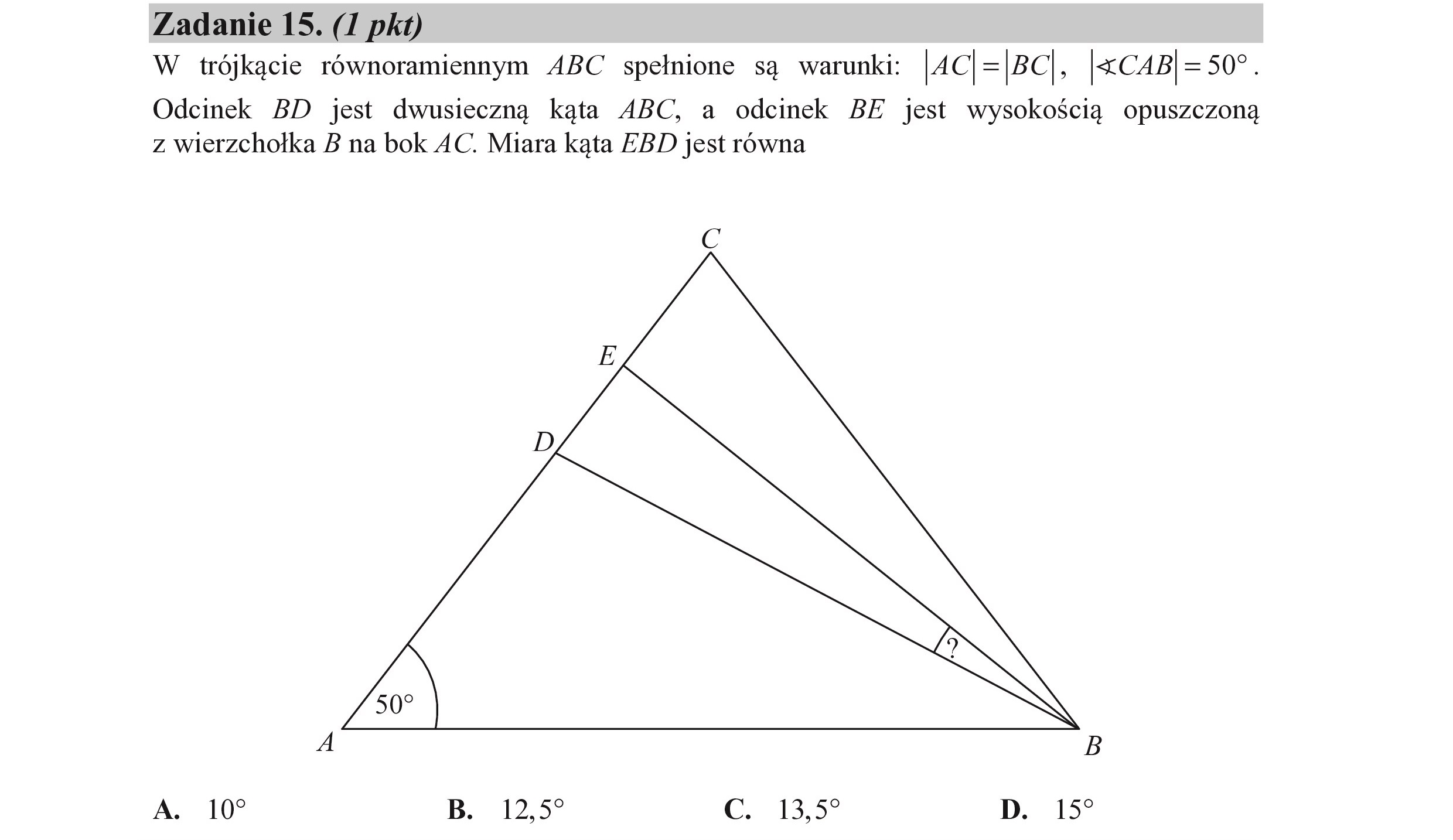
Zadanie 15. (I pkt)
W trójkącie równoramiennym ABC spełnione są warunki: |AC |=|BC
, |<
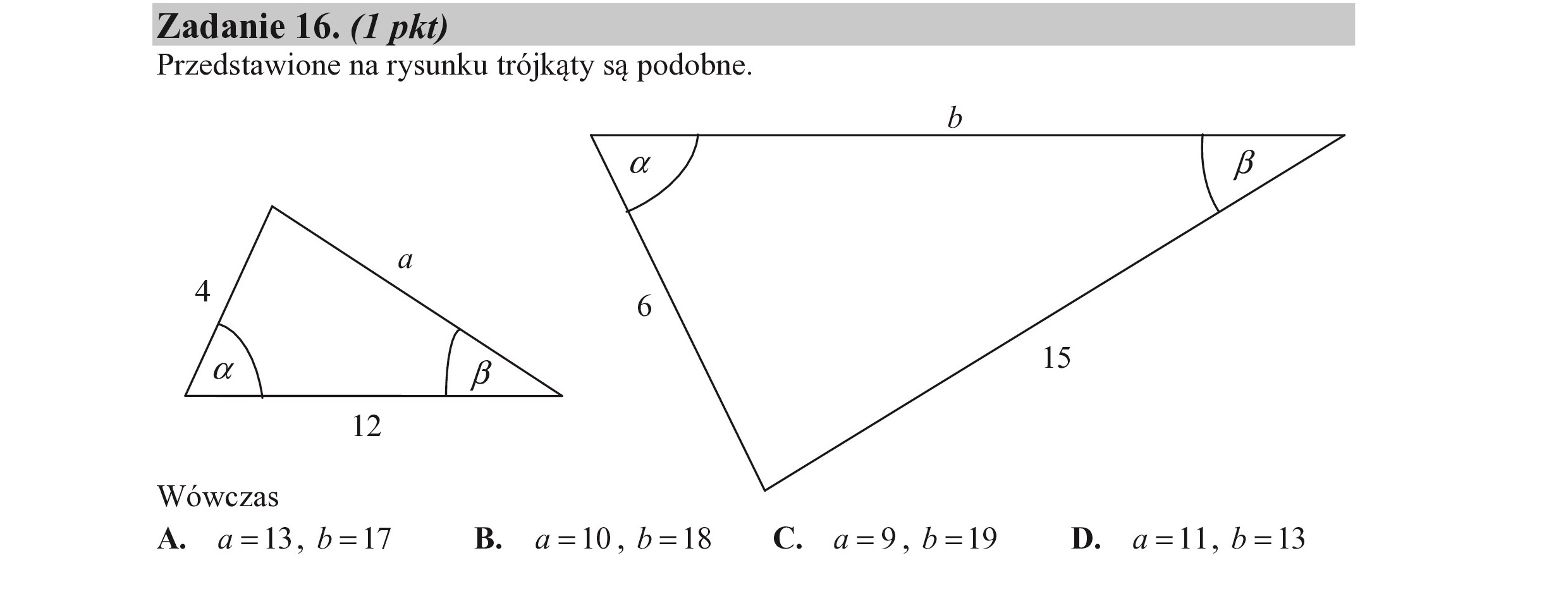
Zadanie 16. (I pkt) Przedstawione na rysunku trójkąty są podobne. b a 4 6 /a) BR 5 12 Wówczas A. a=l13,b=l7 B. a=10,b=18 C. a=9,b=19 D. a=ll,b=13

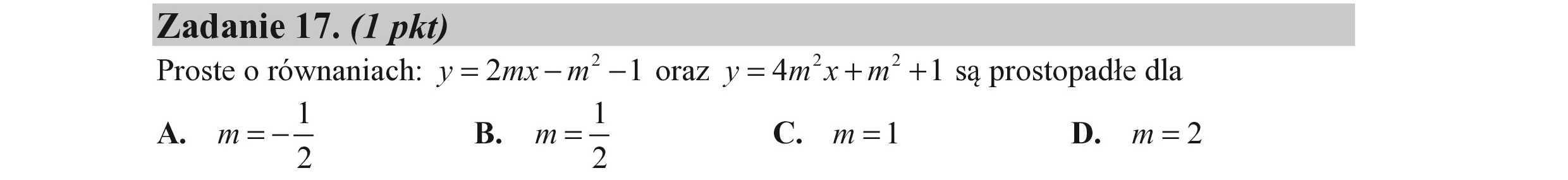
Zadanie 17. (I pkt) Proste o równaniach: y=2mx—m' —l oraz y=4mx+m' +1 są prostopadłe dla l A. m=—— B. = C. m=l D. m=2 2 2


Zadanie 18. (I pkt) Dane są punkty M =(3, -5) oraz N=(—1, 7). Prosta przechodząca przez te punkty ma równanie A. y=-3x+4 B. y=3x-4 c. y=-zx+4 D. y=3x+4

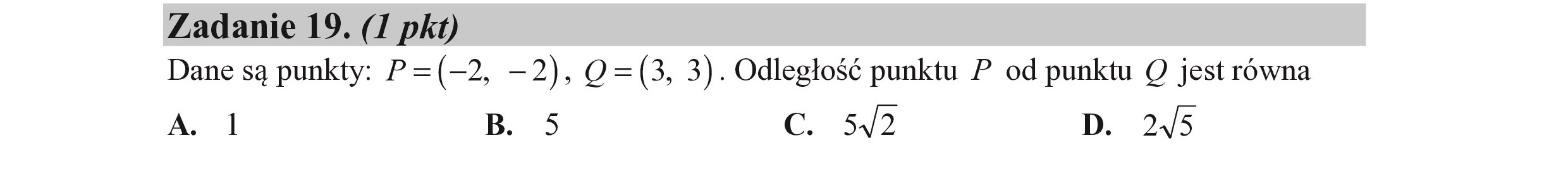
Zadanie 19. (I pkt) Dane są punkty: P=(—2, —2), Q=(3, 3). Odległość punktu P od punktu © jest równa A. 1 B. 5 Cc. 5J2 D. 245


Zadanie 20. (I pkt) Punkt K =(—4,4) jest końcem odcinka KZ, punkt Z leży na osi Ox, a środek S tego odcinka leży na osi Oy. Wynika stąd, że A. S=(0,2) B. S=(-2,0) Cc. S=(4,0) D. S=(0, 4)

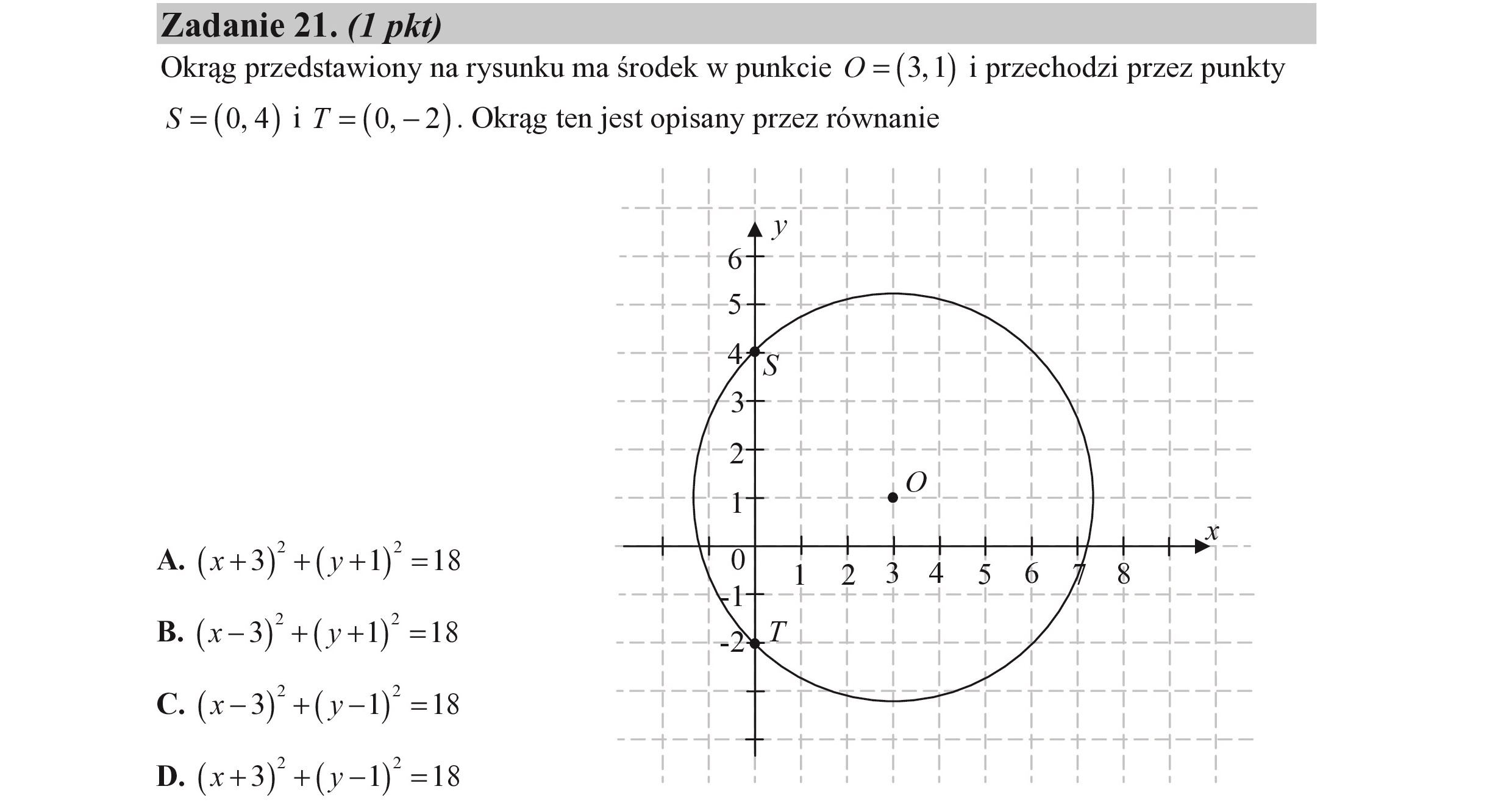
Zadanie 21. (I pkt) Okrąg przedstawiony na rysunku ma środek w punkcie O =(3, 1) i przechodzi przez punkty S=(0,4) i T=(0,—2). Okrąg ten jest opisany przez równanie A. (x+3) +(y+1) =18 B. (x-3) +(v+1) =18 C. (x-3) +(y-1) =18 D. (x+3) +(y-1) =18


Zadanie 22. (I pkt) Przekątna Ściany sześcianu ma długość 2. Pole powierzchni całkowitej tego sześcianu jest równe A. 24 B. 1242 Cc 12 D. 16/2


Zadanie 23. (I pkt) Kula o promieniu 5cm i stożek o promieniu podstawy 10 cm mają równe objętości. Wysokość stożka jest równa A. Zm B. l0cm c. M m D. 5cm T T


Zadanie 24. (I pkt) Średnia arytmetyczna zestawu danych: 2, 4, 7, 8,9 jest taka sama jak średnia arytmetyczna zestawu danych: 2, 4, 7, 8,9, x. Wynika stąd, że A. x=0 B. x=3 C. x=5


Zadanie 25. (I pkt) W pewnej klasie stosunek liczby dziewcząt do liczby chłopców jest równy 4:5. Losujemy jedną osobę z tej klasy. Prawdopodobieństwo tego, że będzie to dziewczyna, jest równe A. Ź B. Ż , > p. - 3 3 4 3


Zadanie 26. (2 pkt) Wykaż, że dla każdej liczby rzeczywistej x i dla każdej liczby rzeczywistej y prawdziwa jest nierówność 4x —8xv+5y 20.


Zadanie 27. (2 pkt) w 5 . 7 rz 2 Rozwiąż nierówność 2x —4x2x—2.


Zadanie 28. (2 pkt) Rozwiąż równanie 4x) +4x —x-1=0.

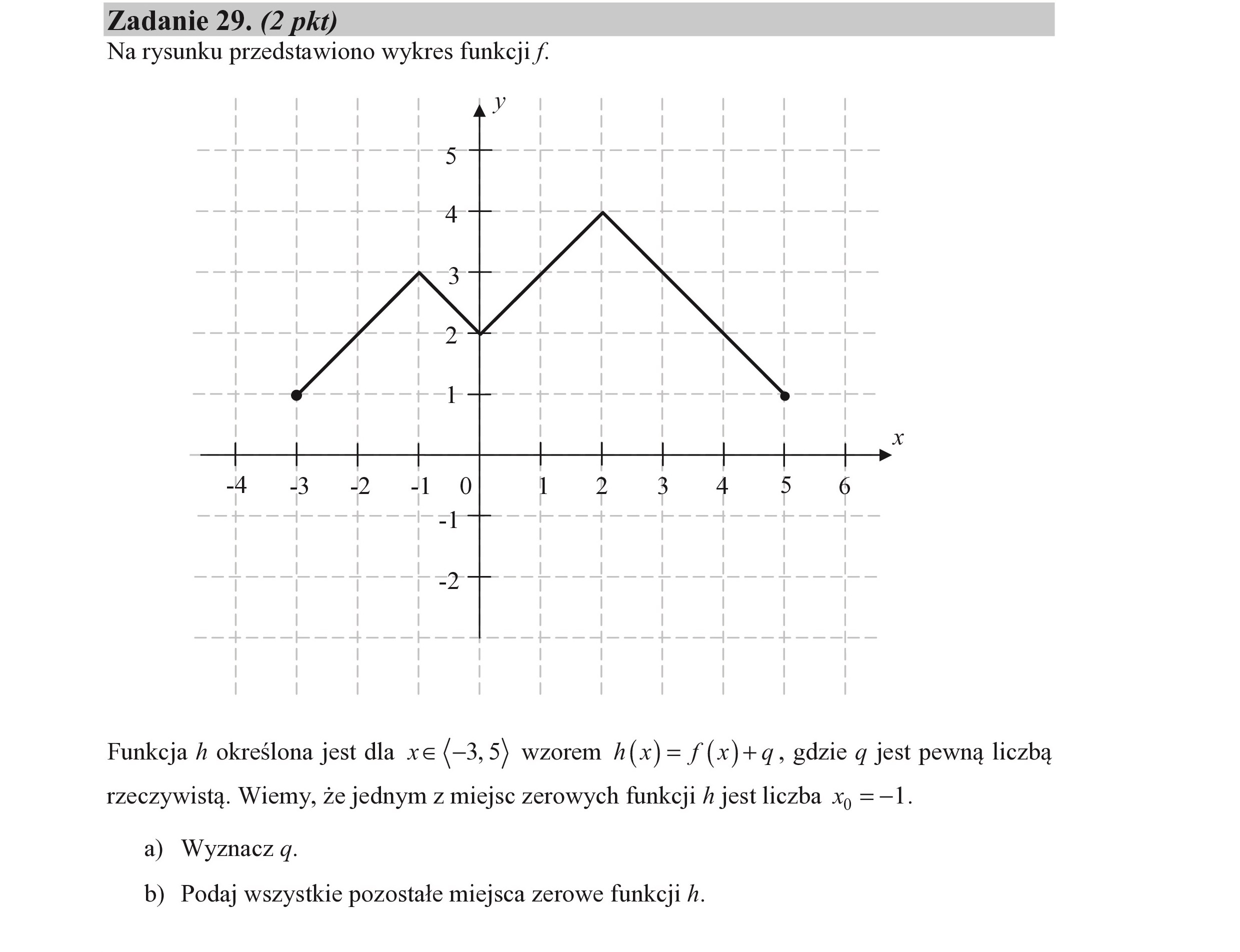
Zadanie 29. (2 pkt) Na rysunku przedstawiono wykres funkcji f. e Funkcja h określona jest dla xe (—3,5) wzorem h(x)= /(x)+q, gdzie q jest pewną liczbą rzeczywistą. Wiemy, że jednym z miejsc zerowych funkcji h jest liczba x, =—1. a) Wyznacz q. b) Podaj wszystkie pozostałe miejsca zerowe funkcji h.

Zadanie 30. (2 pkt) Dany jest skończony ciąg, w którym pierwszy wyraz jest równy 444, a ostatni jest równy 653. Każdy wyraz tego ciągu, począwszy od drugiego, jest o 11 większy od wyrazu bezpośrednio go poprzedzającego. Oblicz sumę wszystkich wyrazów tego ciągu.

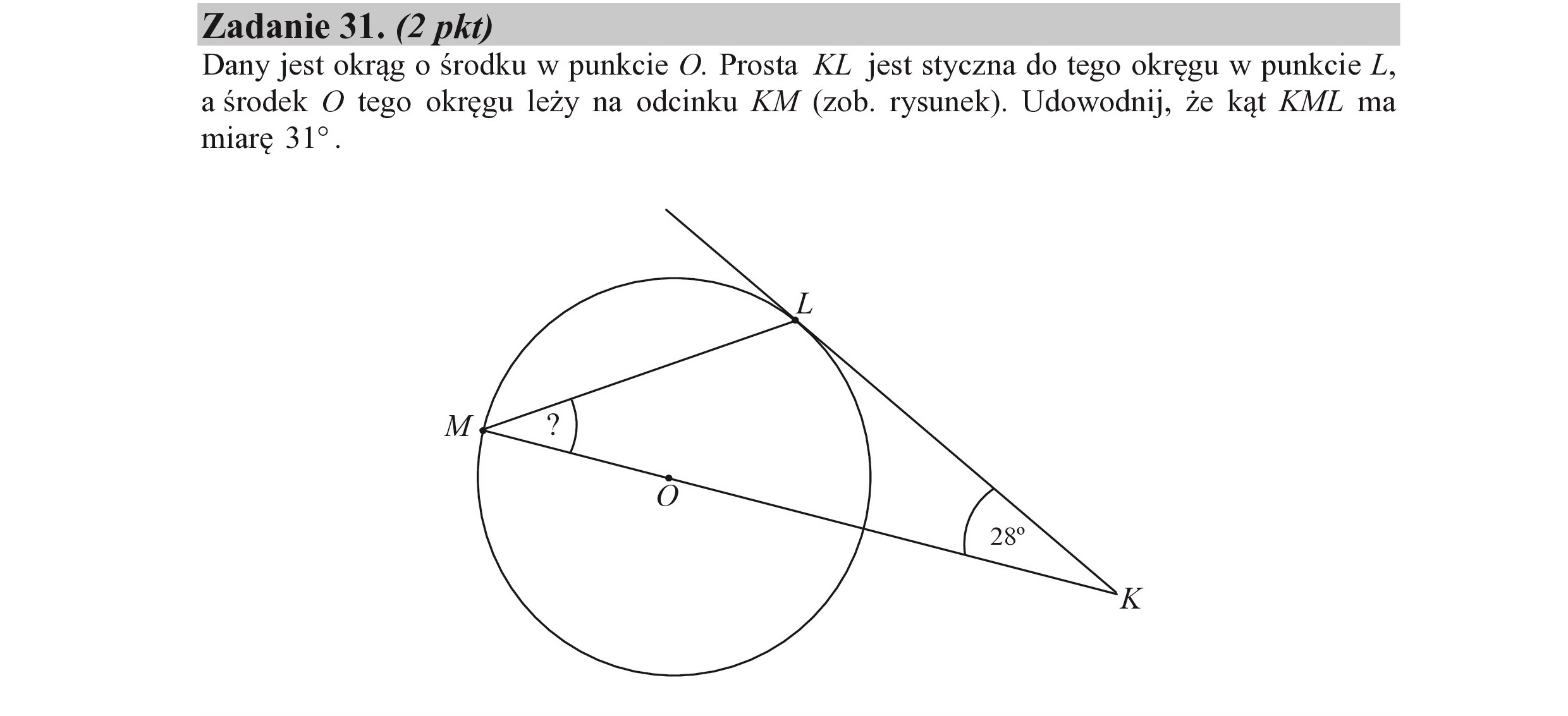
Zadanie 31. (2 pkt) Dany jest okrąg o środku w punkcie O. Prosta KZ jest styczna do tego okręgu w punkcie Z, a środek O tego okręgu leży na odcinku KM (zob. rysunek). Udowodnij, że kąt KML ma miarę 310.


Zadanie 32. (4 pkt) Wysokość graniastosłupa prawidłowego czworokątnego jest równa 16. Przekątna graniastosłupa ; : md 3 : jest nachylona do płaszczyzny jego podstawy pod kątem, którego cosinus jest równy go Oblicz pole powierzchni całkowitej tego graniastosłupa.


Zadanie 33. (4 pkt) Wśród 115 osób przeprowadzono badania ankietowe, związane z zakupami w pewnym kiosku. W poniższej tabeli przedstawiono informacje o tym, ile osób kupiło bilety tramwajowe ulgowe oraz ile osób kupiło bilety tramwajowe normalne. Rodzaj kupionych Liczba osób biletów ulgowe 76 normalne | 41 | Uwaga! 27 osób spośród ankietowanych kupiło oba rodzaje biletów. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że osoba losowo wybrana spośród ankietowanych nie kupiła żadnego biletu. Wynik przedstaw w formie nieskracalnego ułamka.


Zadanie 34. (5 pkt) Biegacz narciarski Borys wyruszył na trasę biegu o 10 minut później niż inny zawodnik, Adam. Metę zawodów, po przebyciu 15-kilometrowej trasy biegu, obaj zawodnicy pokonali równocześnie. Okazało się, że wartość średniej prędkości na całej trasie w przypadku Borysa była o 4,5 e większa niż w przypadku Adama. Oblicz, w jakim czasie Adam pokonał całą trasę biegu.

MATEMATYKA 2015 MAJ MATURA STARA PODSTAWOWA

Zadanie 1. (I pkt) Cena pewnego towaru wraz z 7-procentowym podatkiem VAT jest równa 34 347 zł. Cena tego samego towaru wraz z 23-procentowym podatkiem VAT będzie równa A. 37236 zł B. 39842,52 zł C. 39483 zł D. 42 246,81 zł


Zadanie 2. (I pkt) Najmniejszą liczbą całkowitą dodatnią spełniającą nierówność |r+ 4,5 26 jest A. x=l B. x=2 C. 5=3 D. x=6


4 Liczba 23 -V2' jest równa A. 23 B. 2 GG 2 D. 2


Zadanie 4. (I pkt) Liczba 2logz 10— logs; 4 jest równa A. 2 B. logs 96 Cc. 2logs6

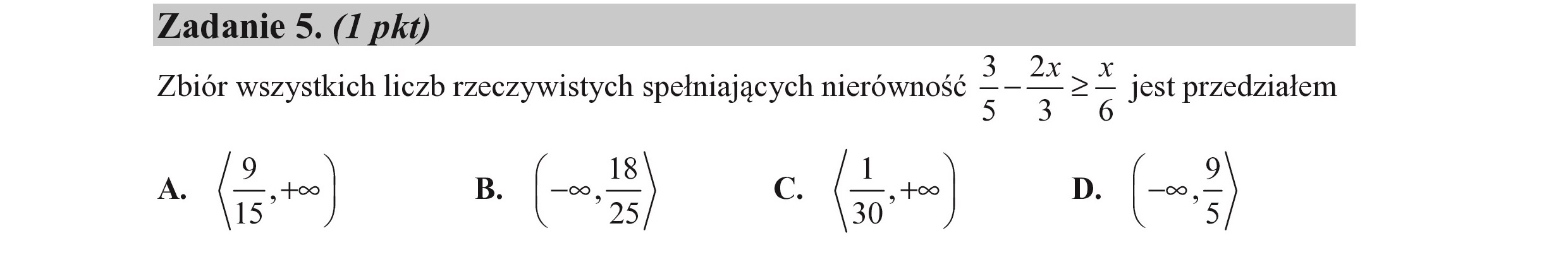
Zadanie 5. (I pkt) Zbiór wszystkich liczb rzeczywistych spełniających nierówność = = 2 5 jest przedziałem A. zo) B. [035 zę) D. ->5 15 23 30 3


Zadanie 6. (I pkt) Bieda hko f deoc wzi flej= 2 Xx — może być zbiór A. wszystkich liczb rzeczywistych różnych od 0 1 od 4. B. wszystkich liczb rzeczywistych różnych od —4 1 od 4. C. wszystkich liczb rzeczywistych różnych od —4 1 od 0. D. wszystkich liczb rzeczywistych.


Zadanie 7. (I pkt) Rozwiązaniem równania A. x=0 4 jest liczba


Zadanie 8. (I pkt) Miejscem zerowym funkcji liniowej określonej wzorem f(x) = —g* +4 jest A. 0 B. 6 C. 4 D. —6


Zadanie 9. (I pkt) l 2" A— : Punkt M -(3: ; należy do wykresu funkcji liniowej określonej wzorem J(3)=(3—2a)x+2. Wtedy A. gp" B. a=2 C. a= 1 D. a= p. 2


Zadanie 10. (I pkt) Na rysunku przedstawiono fragment prostej o równaniu y=ax+b. V = b» w© RE u O MAI %


Zadanie 11. (I pkt) W ciągu arytmetycznym (a) określonym dla n>1 dane są a, =-—4 i r=2. Którym wyrazem tego ciągu jest liczba 156? A. 81. B. 60. C. 76. D. 77.

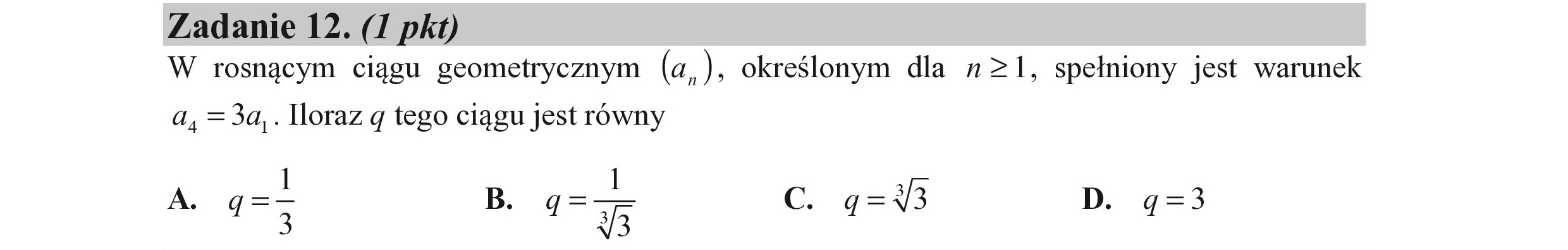
Zadanie 12. (I pkt) W rosnącym ciągu geometrycznym (a,), określonym dla n>1, spełniony jest warunek a, =3a,. lloraz q tego ciągu jest równy A. q=— B. q= C. q=3 D. q=3 3 5|-


Zadanie 13. (I pkt) Drabinę o długości 4 metrów oparto o pionowy mur, a jej podstawę umieszczono w odległości 1,30 m od tego muru (zobacz rysunek). 1,30m Kąt ©, pod jakim ustawiono drabinę, spełnia warunek A. 0O<a<302 B. 30%<a<459 C. 45<a<607 D. 60%<a<907


Zadanie 14. (I pkt) . |. 2 , . ż Kąt a jest ostry 1 sina = rh Wówczas cos a jest równy A. p. JE 5 3 2 4 u|5] —


Zadanie 15. (I pkt) W trójkącie równoramiennym ABC spełnione są warunki: |AC |=|BC , |<<CAB|=509. Odcinek BD jest dwusieczną kąta ABC, a odcinek BE jest wysokością opuszczoną z wierzchołka B na bok AC. Miara kąta EBD jest równa .- A. 107 B. 12,5 C. 13,5? D. 157


Zadanie 16. (I pkt) Przedstawione na rysunku trójkąty są podobne. b a 4 6 /a) BR 5 12 Wówczas A. a=l13,b=l7 B. a=10,b=18 C. a=9,b=19 D. a=ll,b=13

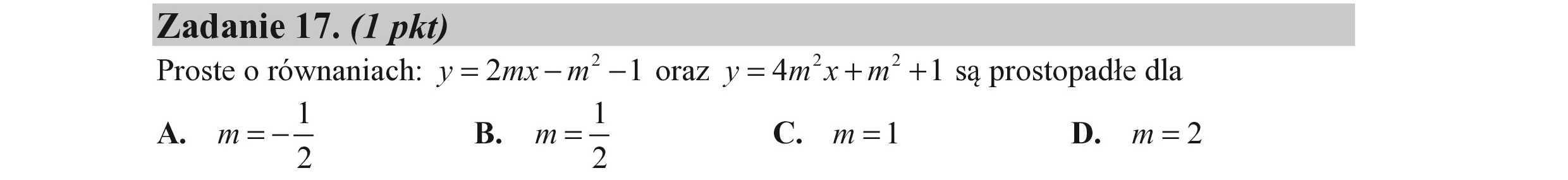
Zadanie 17. (I pkt) Proste o równaniach: y=2mx—m' —l oraz y=4mx+m' +1 są prostopadłe dla l A. m=—— B. = C. m=l D. m=2 2 2


Zadanie 18. (I pkt) Dane są punkty M =(3, -5) oraz N=(—1, 7). Prosta przechodząca przez te punkty ma równanie A. y=-3x+4 B. y=3x-4 c. y=-zx+4 D. y=3x+4

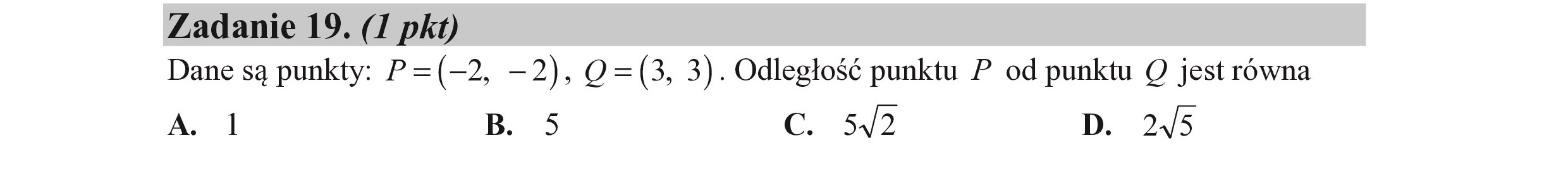
Zadanie 19. (I pkt) Dane są punkty: P=(—2, —2), Q=(3, 3). Odległość punktu P od punktu © jest równa A. 1 B. 5 Cc. 5J2 D. 245


Zadanie 20. (I pkt) Punkt K =(—4,4) jest końcem odcinka KZ, punkt Z leży na osi Ox, a środek S tego odcinka leży na osi Oy. Wynika stąd, że A. S=(0,2) B. S=(-2,0) Cc. S=(4,0) D. S=(0, 4)


Zadanie 21. (I pkt) Okrąg przedstawiony na rysunku ma środek w punkcie O =(3, 1) i przechodzi przez punkty S=(0,4) i T=(0,—2). Okrąg ten jest opisany przez równanie A. (x+3) +(y+1) =18 B. (x-3) +(v+1) =18 C. (x-3) +(y-1) =18 D. (x+3) +(y-1) =18


Zadanie 22. (I pkt) Przekątna Ściany sześcianu ma długość 2. Pole powierzchni całkowitej tego sześcianu jest równe A. 24 B. 1242 Cc 12 D. 16/2


Zadanie 23. (I pkt) Kula o promieniu 5cm i stożek o promieniu podstawy 10 cm mają równe objętości. Wysokość stożka jest równa A. Zm B. l0cm c. M m D. 5cm T T


Zadanie 24. (I pkt) Średnia arytmetyczna zestawu danych: 2, 4, 7, 8,9 jest taka sama jak średnia arytmetyczna zestawu danych: 2, 4, 7, 8,9, x. Wynika stąd, że A. x=0 B. x=3 C. x=5


Zadanie 25. (I pkt) W pewnej klasie stosunek liczby dziewcząt do liczby chłopców jest równy 4:5. Losujemy jedną osobę z tej klasy. Prawdopodobieństwo tego, że będzie to dziewczyna, jest równe A. Ź B. Ż , > p. - 3 3 4 3


Zadanie 26. (2 pkt) Wykaż, że dla każdej liczby rzeczywistej x i dla każdej liczby rzeczywistej y prawdziwa jest nierówność 4x —8xv+5y 20.


Zadanie 27. (2 pkt) w 5 . 7 rz 2 Rozwiąż nierówność 2x —4x2x—2.


Zadanie 28. (2 pkt) Rozwiąż równanie 4x) +4x —x-1=0.


Zadanie 29. (2 pkt) Na rysunku przedstawiono wykres funkcji f. e Funkcja h określona jest dla xe (—3,5) wzorem h(x)= /(x)+q, gdzie q jest pewną liczbą rzeczywistą. Wiemy, że jednym z miejsc zerowych funkcji h jest liczba x, =—1. a) Wyznacz q. b) Podaj wszystkie pozostałe miejsca zerowe funkcji h.

Zadanie 30. (2 pkt) Dany jest skończony ciąg, w którym pierwszy wyraz jest równy 444, a ostatni jest równy 653. Każdy wyraz tego ciągu, począwszy od drugiego, jest o 11 większy od wyrazu bezpośrednio go poprzedzającego. Oblicz sumę wszystkich wyrazów tego ciągu.


Zadanie 31. (2 pkt) Dany jest okrąg o środku w punkcie O. Prosta KZ jest styczna do tego okręgu w punkcie Z, a środek O tego okręgu leży na odcinku KM (zob. rysunek). Udowodnij, że kąt KML ma miarę 310.


Zadanie 32. (4 pkt) Wysokość graniastosłupa prawidłowego czworokątnego jest równa 16. Przekątna graniastosłupa ; : md 3 : jest nachylona do płaszczyzny jego podstawy pod kątem, którego cosinus jest równy go Oblicz pole powierzchni całkowitej tego graniastosłupa.


Zadanie 33. (4 pkt) Wśród 115 osób przeprowadzono badania ankietowe, związane z zakupami w pewnym kiosku. W poniższej tabeli przedstawiono informacje o tym, ile osób kupiło bilety tramwajowe ulgowe oraz ile osób kupiło bilety tramwajowe normalne. Rodzaj kupionych Liczba osób biletów ulgowe 76 normalne | 41 | Uwaga! 27 osób spośród ankietowanych kupiło oba rodzaje biletów. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że osoba losowo wybrana spośród ankietowanych nie kupiła żadnego biletu. Wynik przedstaw w formie nieskracalnego ułamka.


Zadanie 34. (5 pkt) Biegacz narciarski Borys wyruszył na trasę biegu o 10 minut później niż inny zawodnik, Adam. Metę zawodów, po przebyciu 15-kilometrowej trasy biegu, obaj zawodnicy pokonali równocześnie. Okazało się, że wartość średniej prędkości na całej trasie w przypadku Borysa była o 4,5 e większa niż w przypadku Adama. Oblicz, w jakim czasie Adam pokonał całą trasę biegu.






























