MATEMATYKA 2014 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (1 pkt) Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej. A WENA 8 7 22. x A. |x-7|<15 B. |x-7|>15 C. |x-15|<7 D. |x-15|>7


Zadanie 2. (I pkt) . l . Liczba ch 27M jest równa A. 22013 B. 22012 C. 21007 D. j2014

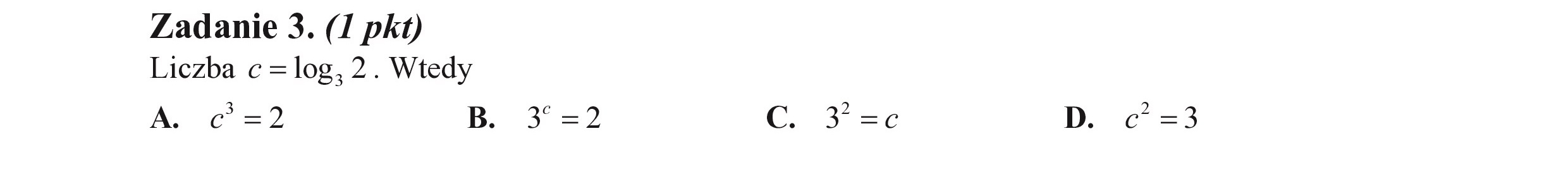
Zadanie 3. (I pkt) Liczba c=log, 2. Wtedy A. C=2 B. 3 =2


Zadanie 4. (I pkt) Liczba (5 —AB ) +2415 jest równa A. 2+2415 B. 8 C. 2+415 D.


Zadanie 5. (I pkt) Julia połowę swoich oszczędności przeznaczyła na prezent dla Maćka. 10% tego, co jej zostało, przeznaczyła na prezent dla Dominiki. Ile procent oszczędności pozostało Julii? A. 25 B. 40 C. 45 D. 55

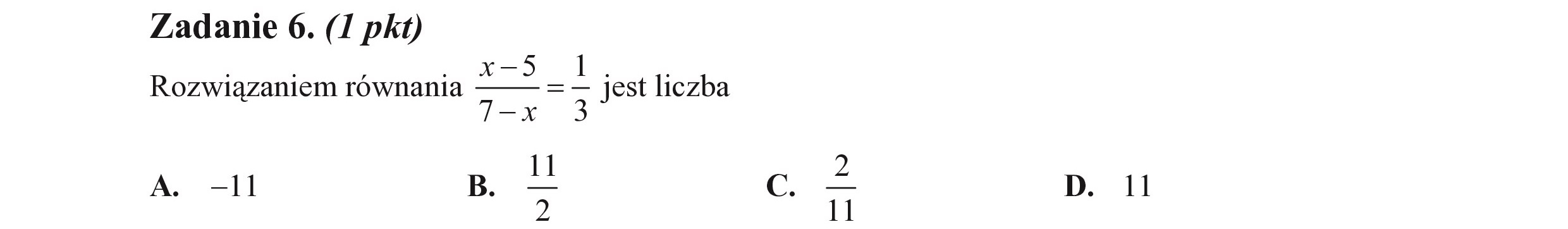
Zadanie 6. (I pkt) ! . , „ x-—S l, | Rozwiązaniem równania 7 = 3 jest liczba =X 11 p A. -1l B. — GG — 2 11 11

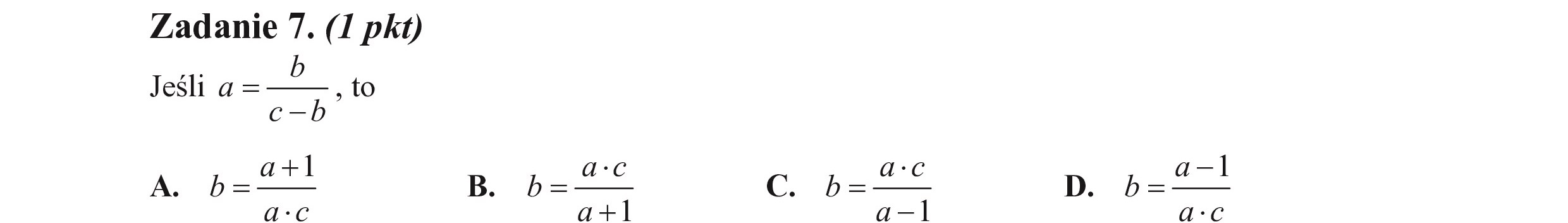
Zadanie 7. (I pkt) Jeśli a = , to c— bl a:c a:c A. b=—— B. b=—— a:C a+l a—l

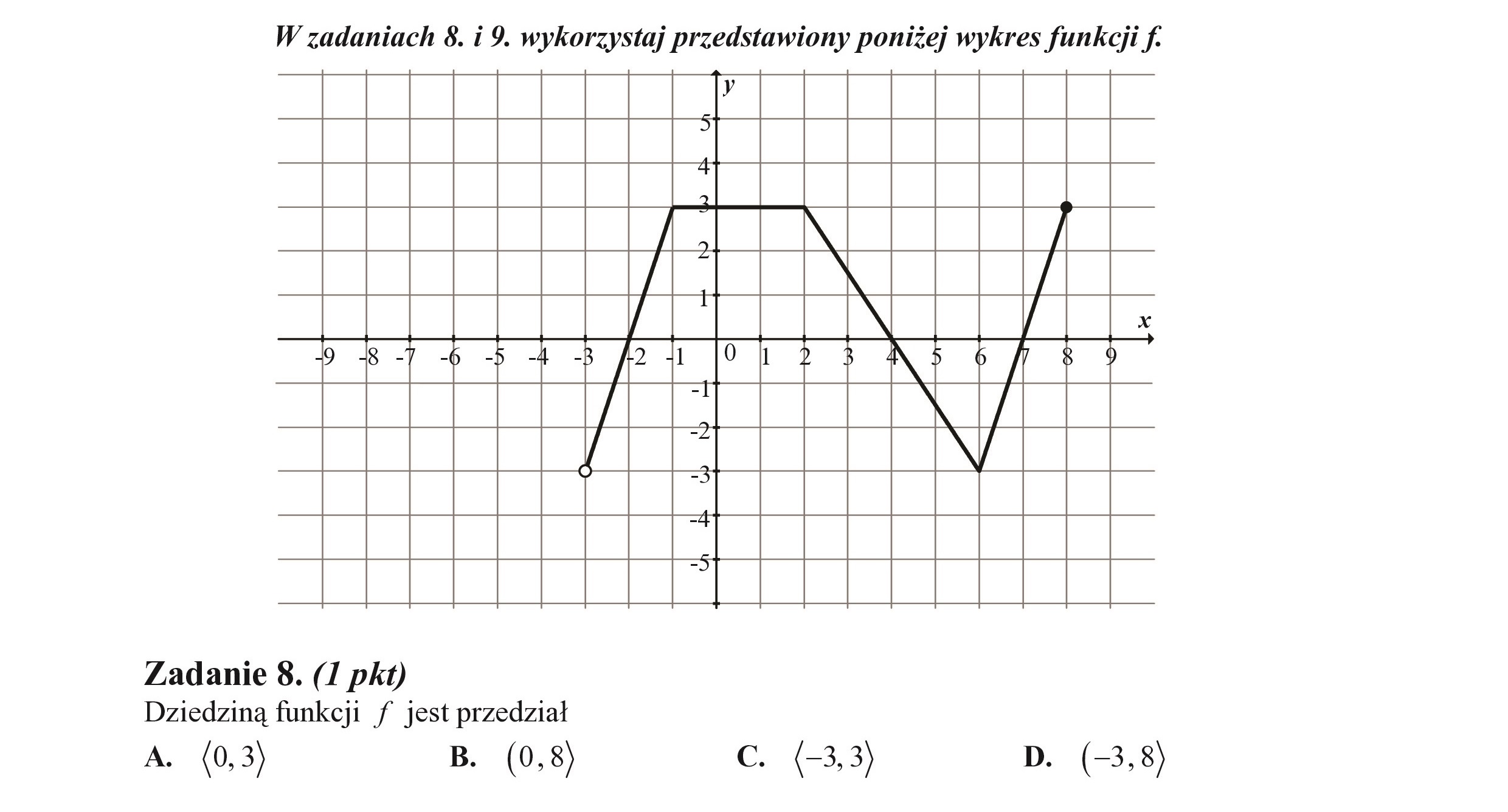
W zadaniach 8. i 9. wykorzystaj przedstawiony poniżej wykres funkcji f. y ZZEZZEJZNUEZENZEJEE Zadanie 8. (I pkt) Dziedziną funkcji f jest przedział A. (0,3) B. (0,8) C. (-3,3) D. (-3,8)

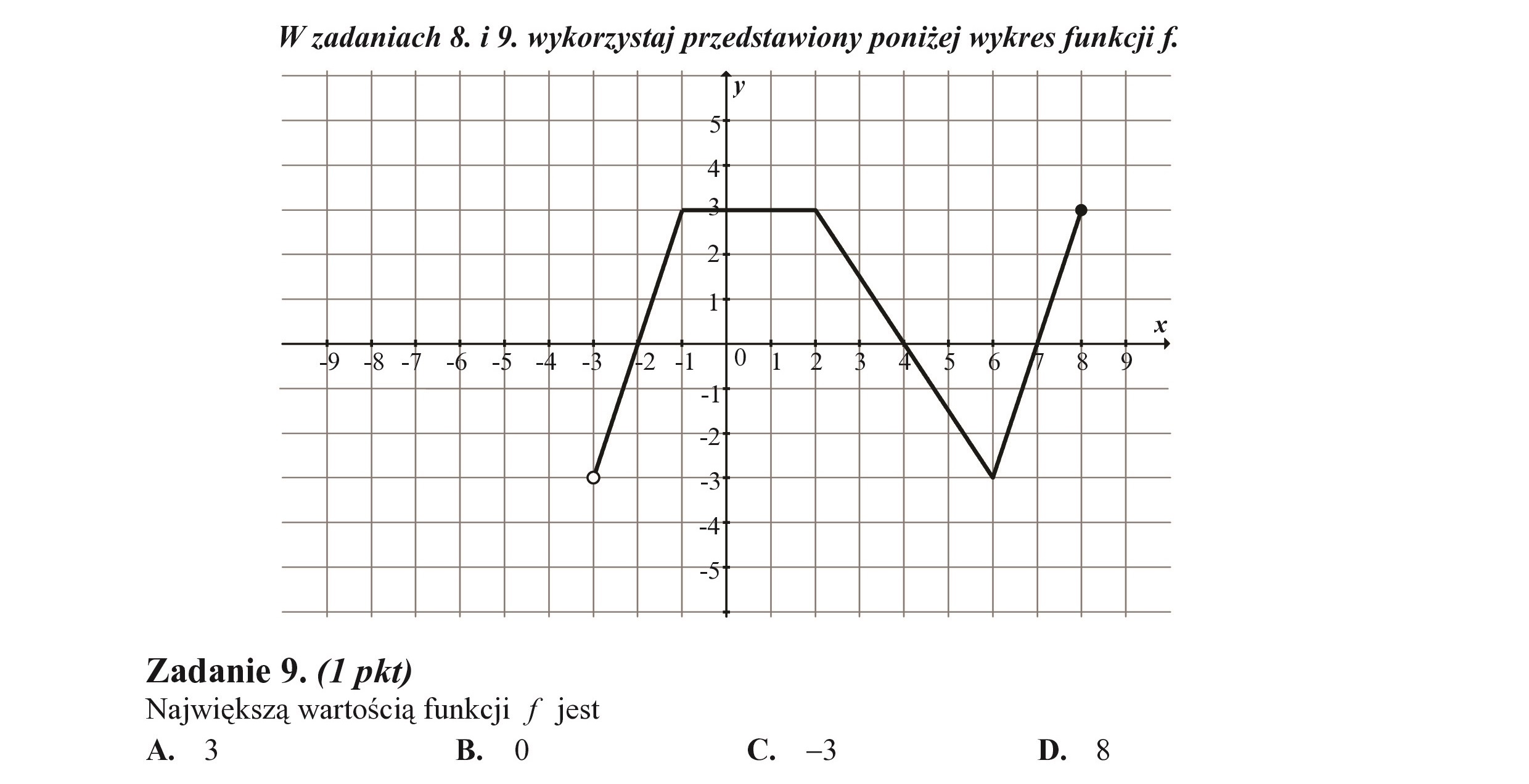
W zadaniach 8. i 9. wykorzystaj przedstawiony poniżej wykres funkcji f. y 2 21 Zadanie 9. (I pkt) Największą wartością funkcji f jest A. 3 B. 0 C. -3 D. 8 N

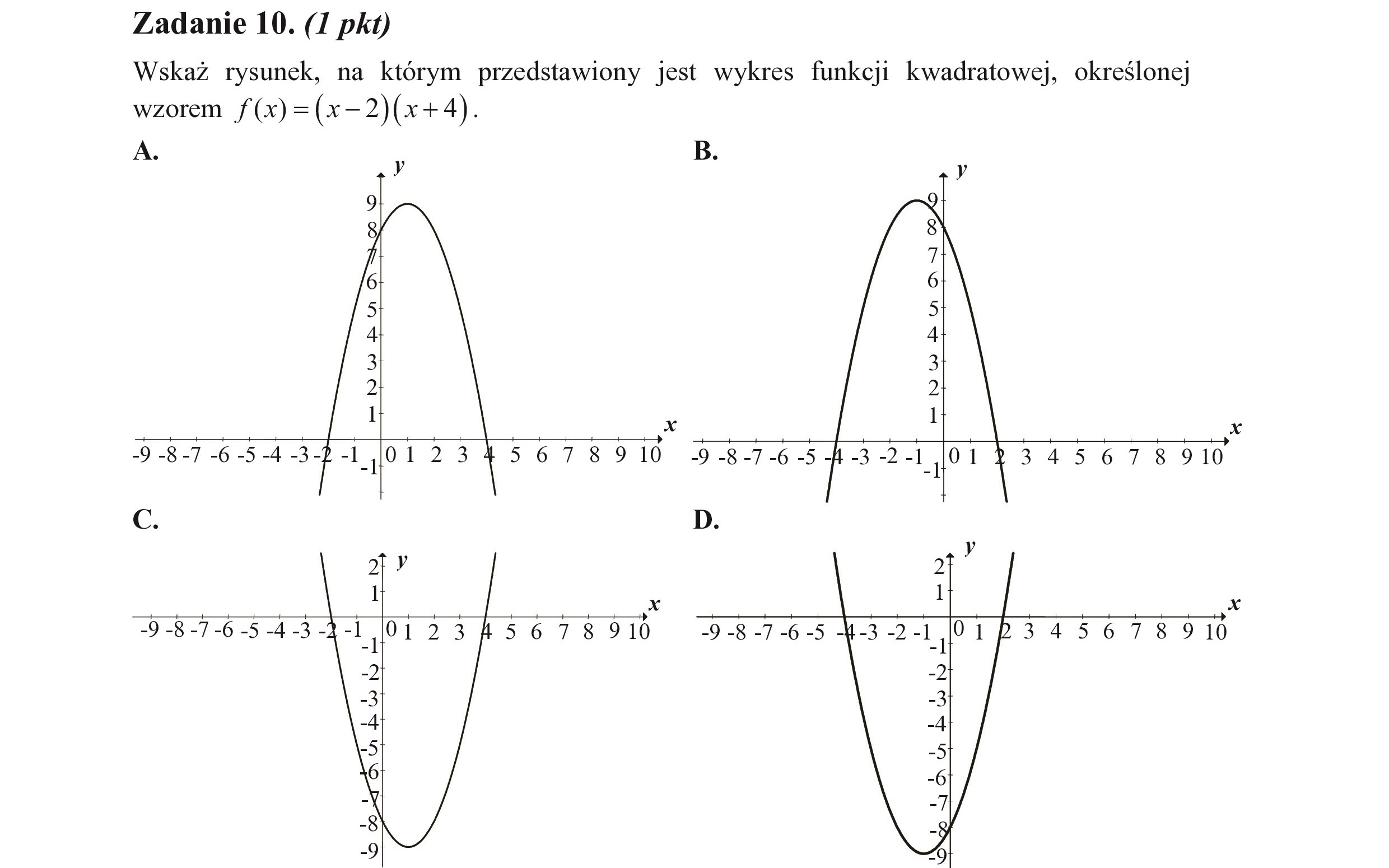
Zadanie 10. (I pkt) Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem f(x) =(x-2)(x+4). A. x B. —NVNWAEBUOdWE 5 BF 6 Ś-4 83 5678 910 x 56 78 910 9 -8-7 -6 -5 jt -3 -2-1 -9 -8 -7 -6 -5 - -3 -2 1 -2 -31 -4 -5 -6 345678 910 x

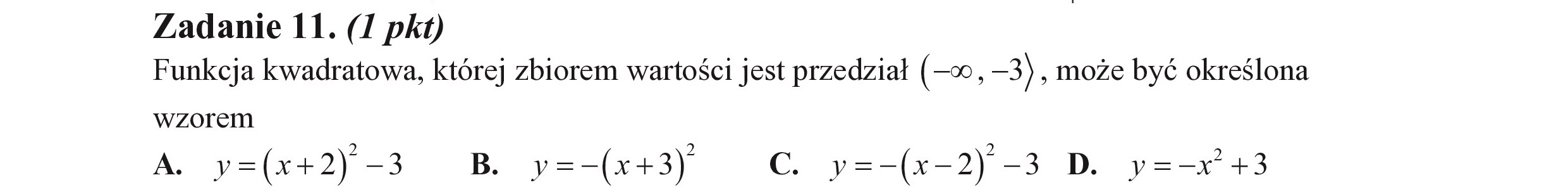
Zadanie 11. (I pkt) Funkcja kwadratowa, której zbiorem wartości jest przedział (©, —3) , może być określona wzorem A. y=(x+2) -3 B. y=-(x+3) Cc. y=-(x-2) -3 D. y=—x +3


Zadanie 12. (I pkt) Funkcja liniowa f(x) = ax +b jest rosnąca i ma dodatnie miejsce zerowe. Stąd wynika, że A. a>0ib>0 B. a<0ib<0 C. a<0ib>0 D. a>0ib<0

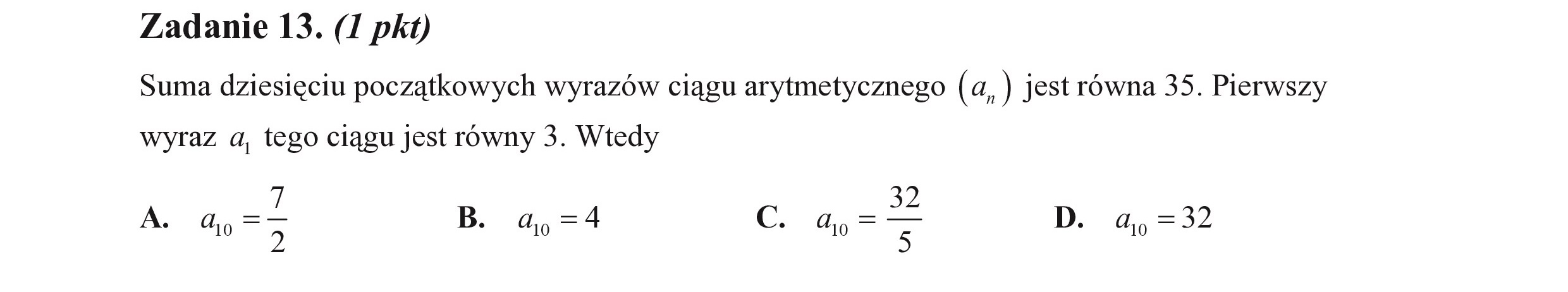
Zadanie 13. (I pkt) Suma dziesięciu początkowych wyrazów ciągu arytmetycznego (a, ) jest równa 35. Pierwszy wyraz a, tego ciągu jest równy 3. Wtedy A. a, ac B. a„,=4 Cc. a,=— D. a,=32


Zadanie 14. (I pkt) n Ciąg geometryczny (a, ) określony jest wzorem a, = "4 dla n>1. Iloraz tego ciągu jest równy A. -3 B. — a|w

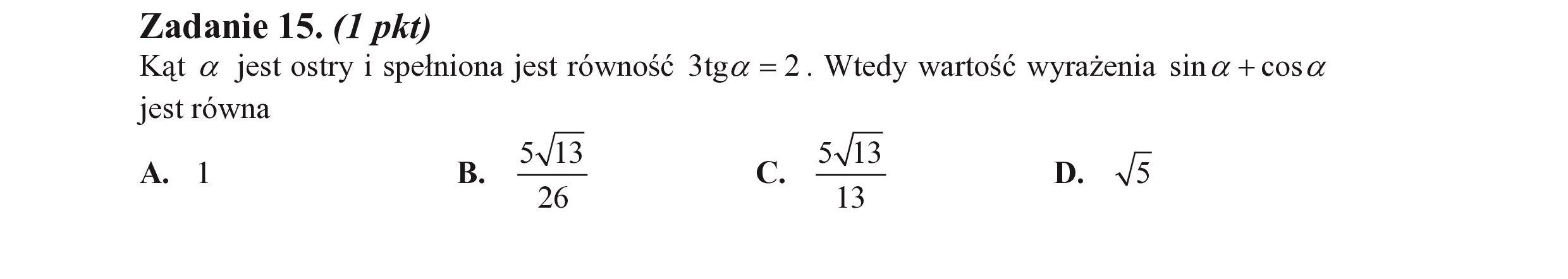
Zadanie 15. (I pkt) Kąt a jest ostry i spełniona jest równość J3tga =2. Wtedy wartość wyrażenia Sina + cosa WE SIENIE 5. 6 26 13 jest równa A. I B.


Zadanie 16. (7 pkt) Promień okręgu opisanego na trójkącie równobocznym jest równy 8. Wysokość tego trójkąta jest równa A. 4/3 B. 843 c. 12 D. 6

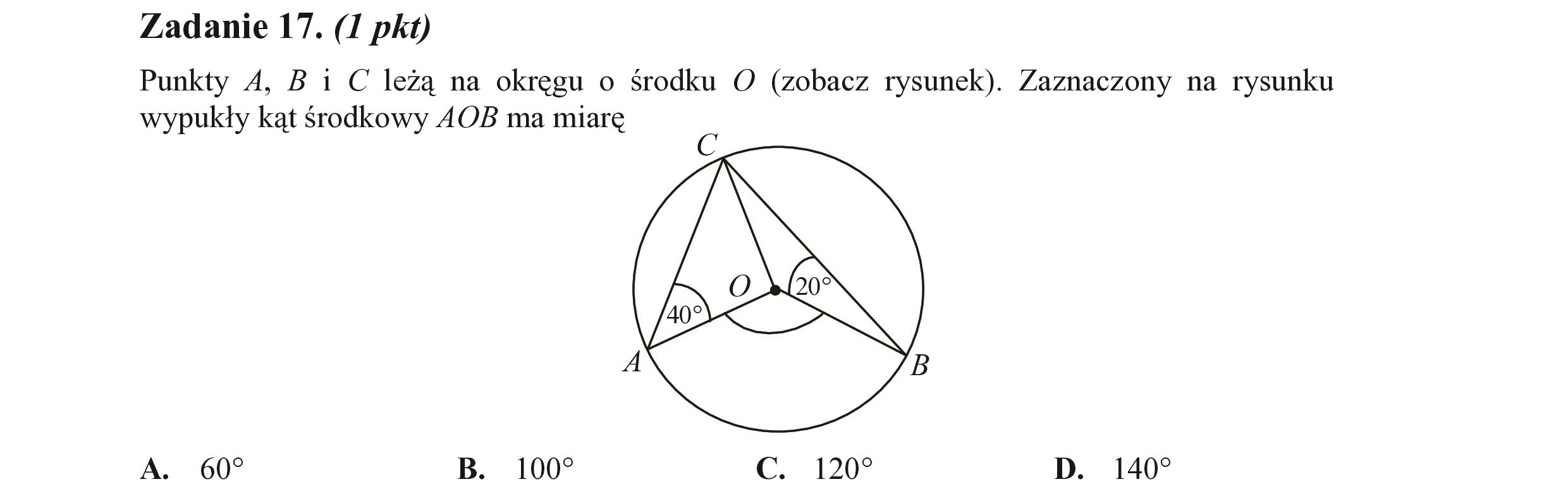
Zadanie 17. (I pkt) Punkty 4, B i C leżą na okręgu o środku O (zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy AOB ma miarę (pa) A. 60 B. 100? c. 120? D. 140?

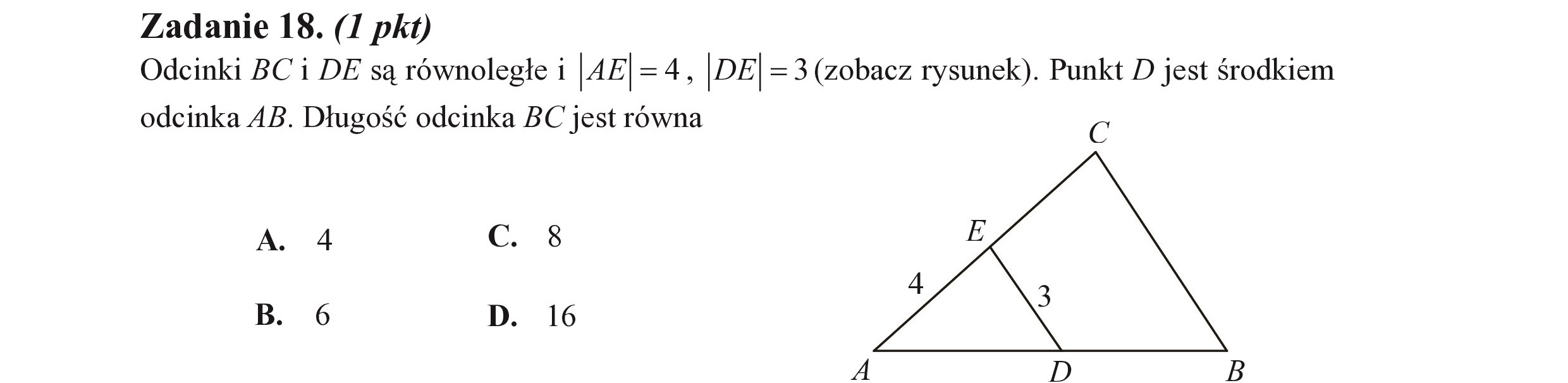
Zadanie 18. (I pkt) Odcinki BC i DE są równoległe i |4E | =4, odcinka AB. Długość odcinka BC jest równa DE | = 3 (zobacz rysunek). Punkt D jest środkiem C

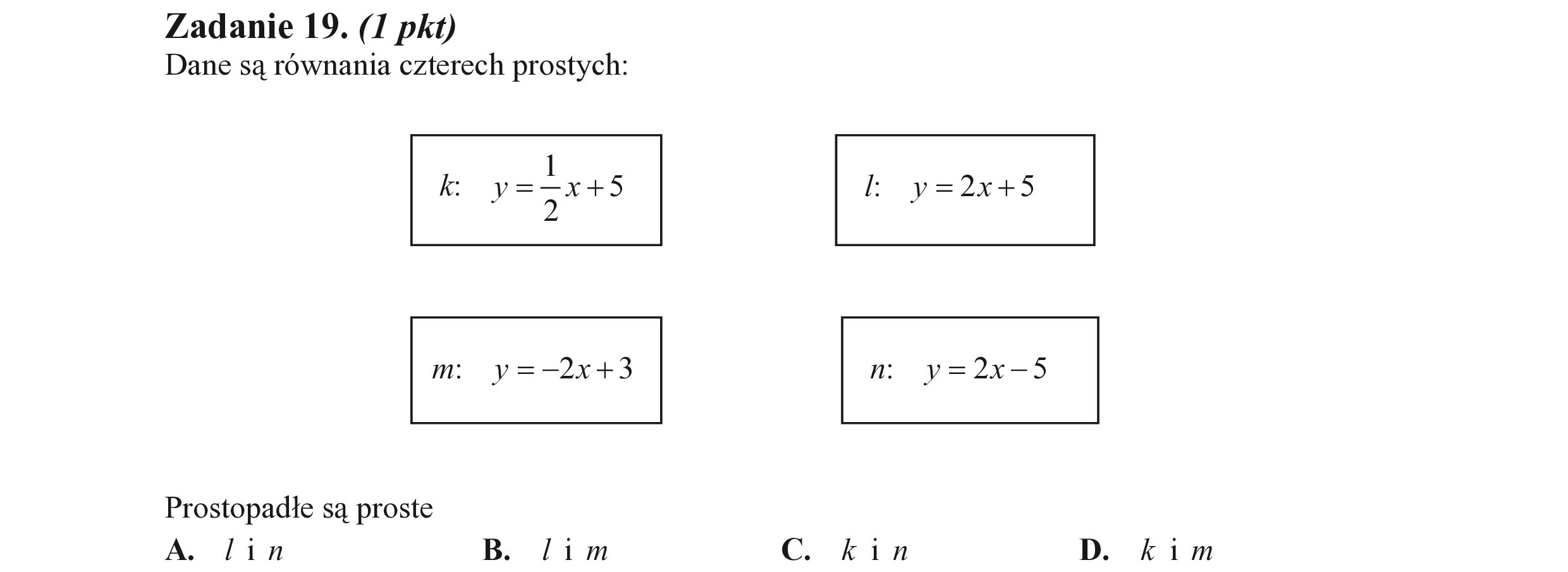
Zadanie 19. (I pkt) Dane są równania czterech prostych: Prostopadłe są proste A. lin B. Jim C. kin D. kim


Zadanie 20. (I pkt) Punkt P=(—1,0) leży na okręgu o promieniu 3. Równanie tego okręgu może mieć postać A. (x+I)+y7=9 B. »x*+(y-N2) =3 C. (x+1) +(y+3) =9 D. (x+1) +y)=3


Zadanie 21. (I pkt) Punkty 4=(13,-12) i C=(15,8) są przeciwległymi wierzchołkami kwadratu ABCD. Przekątne tego kwadratu przecinają się w punkcie A. S=(2,-20) B. S=f(14,10) C. S=(14,-2) D. S=(28,-4)

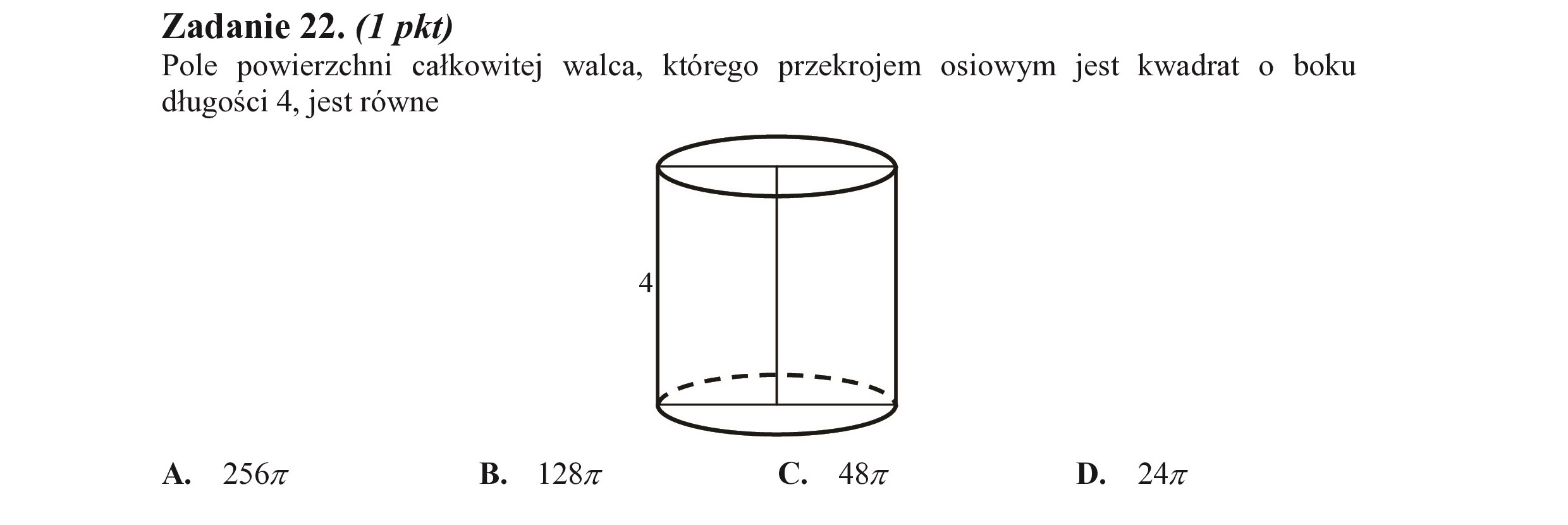
Zadanie 22. (I pkt) Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 4, jest równe A. 2567 B. D. 247


Zadanie 23. (I pkt) Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa Bls/ż, Objętość graniastosłupa jest równa A. 27 B. 2743 C. 243 D. 24343

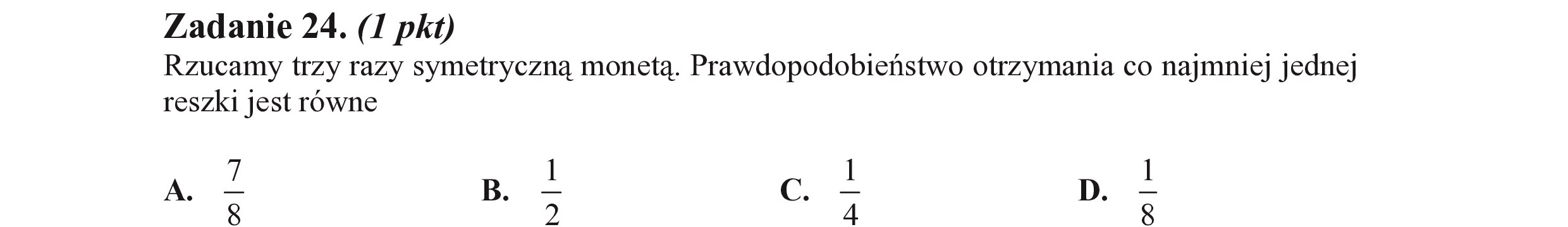
Zadanie 24. (I pkt) Rzucamy trzy razy symetryczną monetą. Prawdopodobieństwo otrzymania co najmniej jednej reszki jest równe A. Ej B. G 8 00 | — . e 7 4


Zadanie 25. (I pkt) Srednia arytmetyczna liczb: x, 13, 7, 5, 5, 3, 2, 11 jest równa 7. Mediana tego zestawu liczb jest równa A. 6 B. 7 Cc. 10 D. 5


Zadanie 26. (2 pkt) Rozwiąż nierówność —x —5x+14<0.


Zadanie 27. (2 pkt) Rozwiąż równanie x —6x —1lx+66=0.

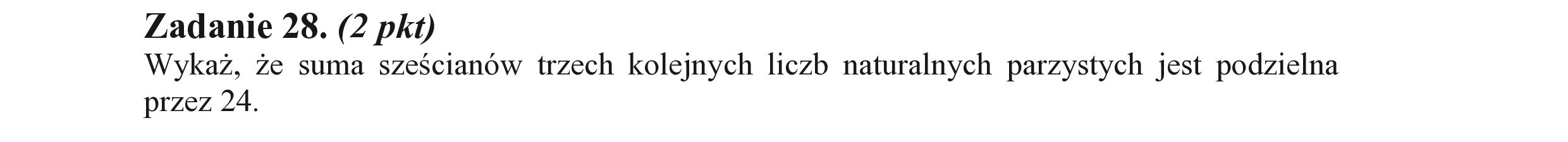
Zadanie 28. (2 pkt) Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych parzystych jest podzielna przez 24.

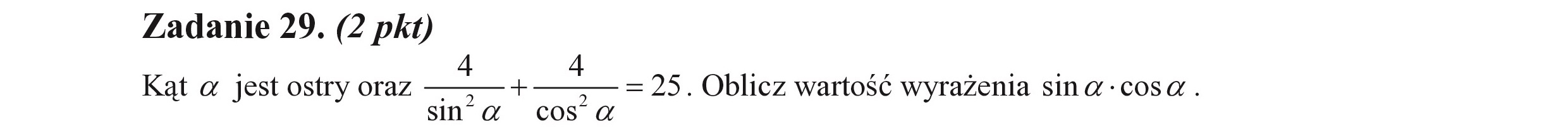
Zadanie 29. (2 pkt) . 4 Kąt a jest ostry oraz + sina cos a = 25. Oblicz wartość wyrażenia sina :cosa.

Zadanie 30. (2 pkt)
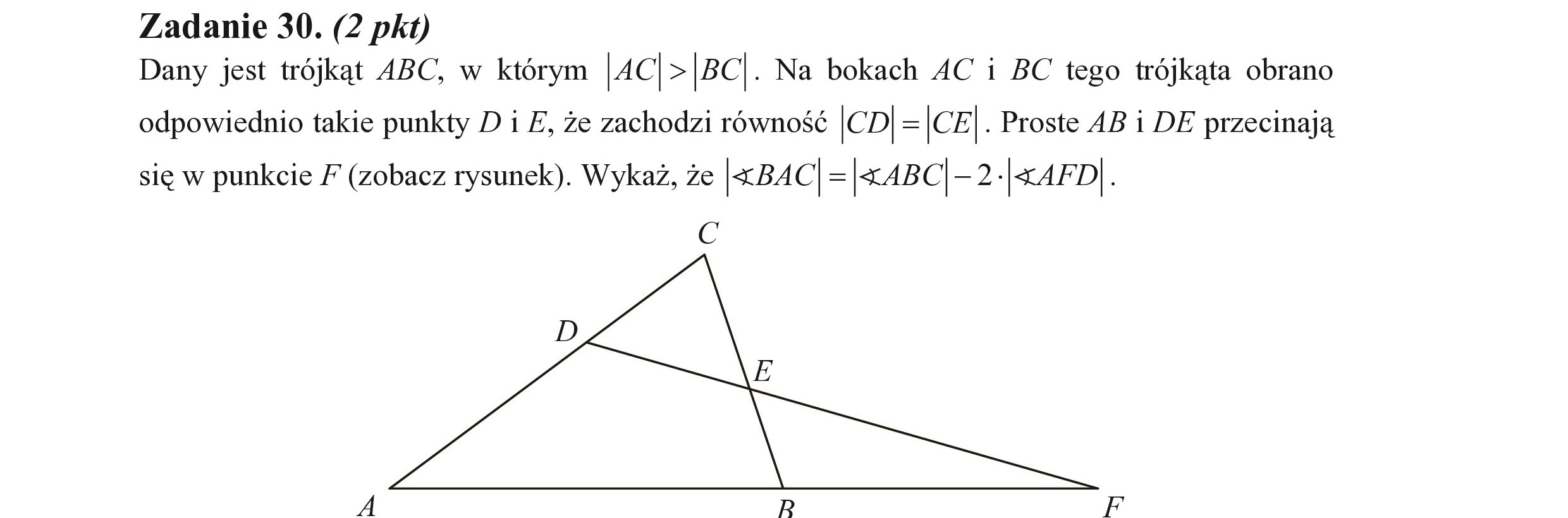
Dany jest trójkąt ABC, w którym |AC|>|BC|. Na bokach AC i BC tego trójkąta obrano
odpowiednio takie punkty D 1 £, że zachodzi równość |CP| = |CE | . Proste AB i DE przecinają
się w punkcie F (zobacz rysunek). Wykaż, że |«BAC| = |
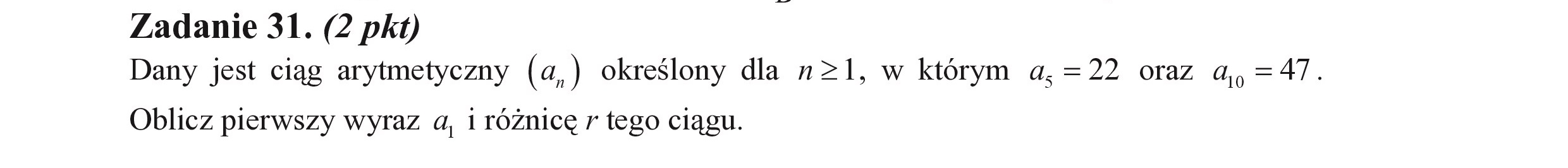
Zadanie 31. (2 pkt) Dany jest ciąg arytmetyczny (a,) określony dla n>l, w którym a, =22 oraz a,=47. Oblicz pierwszy wyraz a, i różnicę r tego ciągu.


Zadanie 32. (5 pkt) Miasta A i B są odległe o 450 km. Pani Danuta pokonała tę trasę swym samochodem w czasie o 75 minut dłuższym niż pani Lidia. Wartość średniej prędkości, z jaką jechała pani Danuta na całej trasie, była o 18 km/h mniejsza od wartości średniej prędkości, z jaką jechała pani Lidia. Oblicz średnie wartości: « prędkości, z jaką pani Danuta jechała z A do B. . prędkości, z jaką pani Lidia jechała z A do B.

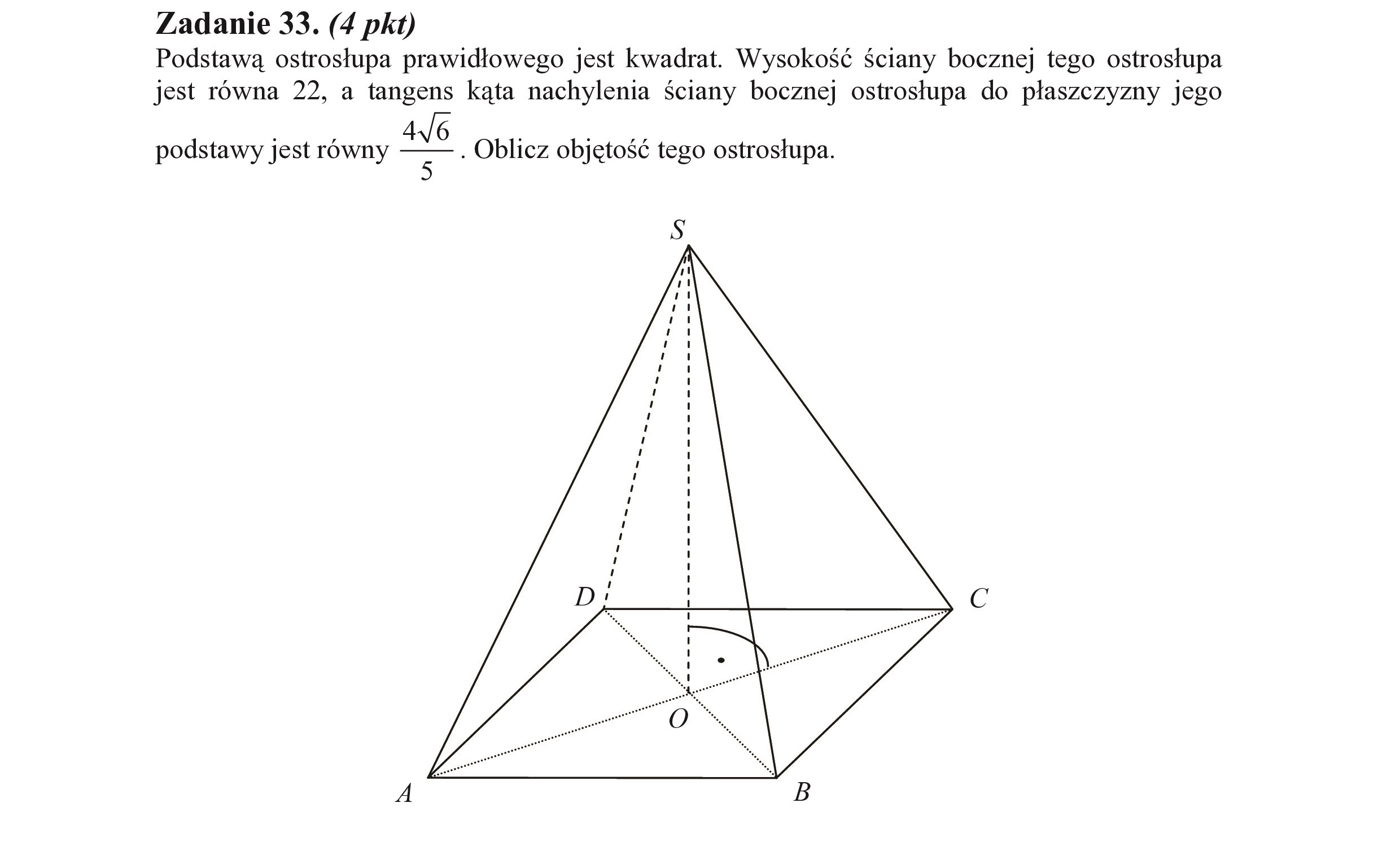
Zadanie 33. (4 pkt) Podstawą ostrosłupa prawidłowego jest kwadrat. Wysokość Ściany bocznej tego ostrosłupa jest równa 22, a tangens kąta nachylenia Ściany bocznej ostrosłupa do płaszczyzny jego . - , . podstawy jest równy SD . Oblicz objętość tego ostrosłupa.


Zadanie 34. (4 pkt) Zbiór M tworzą wszystkie liczby naturalne dwucyfrowe, w zapisie których występują dwie różne cyfry spośród: 1, 2, 3, 4, 5. Ze zbioru M losujemy jedną liczbę, przy czym każda liczba z tego zbioru może być wylosowana ztym samym prawdopodobieństwem. Oblicz prawdopodobieństwo, że wylosujemy liczbę większą od 20, w której cyfra dziesiątek jest mniejsza od cyfry jedności.

MATEMATYKA 2014 SIERPIEN POPRAWKOWA PODSTAWOWA

Zadanie 1. (1 pkt) Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej. A WENA 8 7 22. x A. |x-7|<15 B. |x-7|>15 C. |x-15|<7 D. |x-15|>7


Zadanie 2. (I pkt) . l . Liczba ch 27M jest równa A. 22013 B. 22012 C. 21007 D. j2014

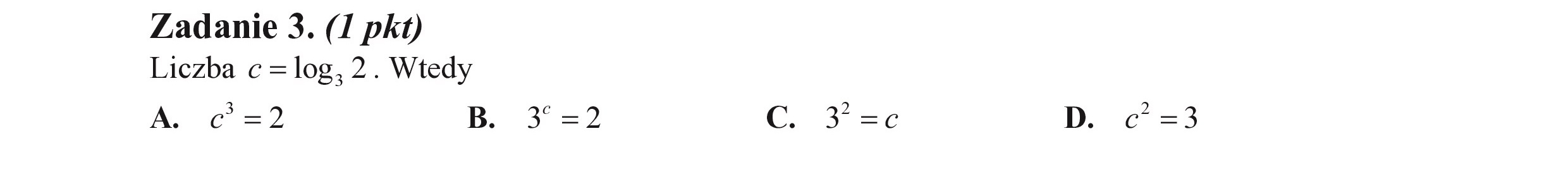
Zadanie 3. (I pkt) Liczba c=log, 2. Wtedy A. C=2 B. 3 =2


Zadanie 4. (I pkt) Liczba (5 —AB ) +2415 jest równa A. 2+2415 B. 8 C. 2+415 D.


Zadanie 5. (I pkt) Julia połowę swoich oszczędności przeznaczyła na prezent dla Maćka. 10% tego, co jej zostało, przeznaczyła na prezent dla Dominiki. Ile procent oszczędności pozostało Julii? A. 25 B. 40 C. 45 D. 55

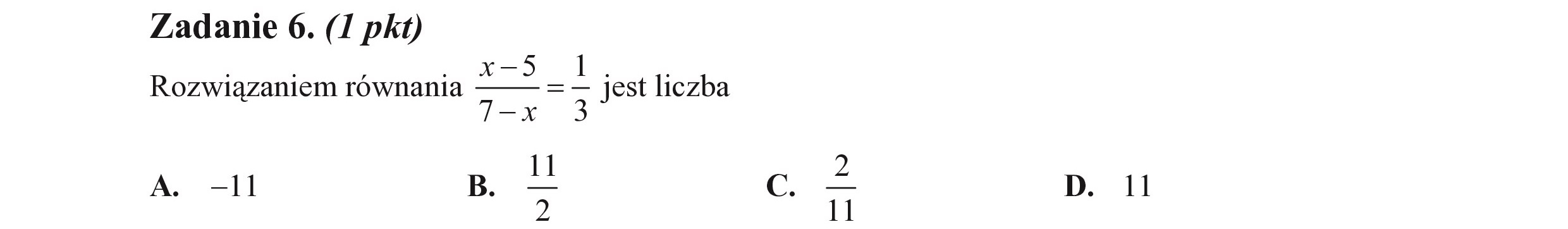
Zadanie 6. (I pkt) ! . , „ x-—S l, | Rozwiązaniem równania 7 = 3 jest liczba =X 11 p A. -1l B. — GG — 2 11 11

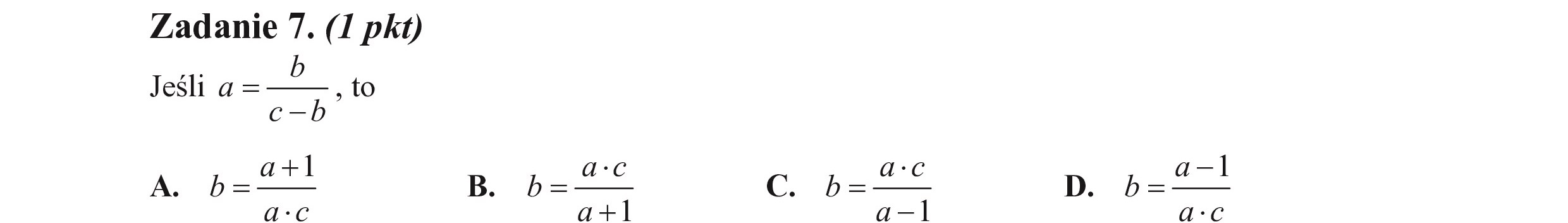
Zadanie 7. (I pkt) Jeśli a = , to c— bl a:c a:c A. b=—— B. b=—— a:C a+l a—l


W zadaniach 8. i 9. wykorzystaj przedstawiony poniżej wykres funkcji f. y ZZEZZEJZNUEZENZEJEE Zadanie 8. (I pkt) Dziedziną funkcji f jest przedział A. (0,3) B. (0,8) C. (-3,3) D. (-3,8)


W zadaniach 8. i 9. wykorzystaj przedstawiony poniżej wykres funkcji f. y 2 21 Zadanie 9. (I pkt) Największą wartością funkcji f jest A. 3 B. 0 C. -3 D. 8 N


Zadanie 10. (I pkt) Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem f(x) =(x-2)(x+4). A. x B. —NVNWAEBUOdWE 5 BF 6 Ś-4 83 5678 910 x 56 78 910 9 -8-7 -6 -5 jt -3 -2-1 -9 -8 -7 -6 -5 - -3 -2 1 -2 -31 -4 -5 -6 345678 910 x

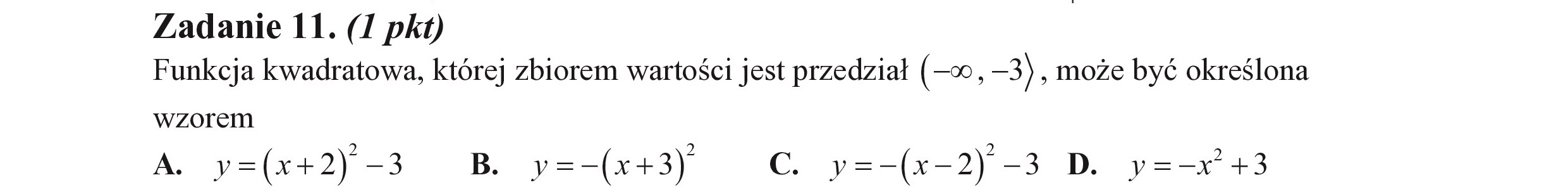
Zadanie 11. (I pkt) Funkcja kwadratowa, której zbiorem wartości jest przedział (©, —3) , może być określona wzorem A. y=(x+2) -3 B. y=-(x+3) Cc. y=-(x-2) -3 D. y=—x +3


Zadanie 12. (I pkt) Funkcja liniowa f(x) = ax +b jest rosnąca i ma dodatnie miejsce zerowe. Stąd wynika, że A. a>0ib>0 B. a<0ib<0 C. a<0ib>0 D. a>0ib<0

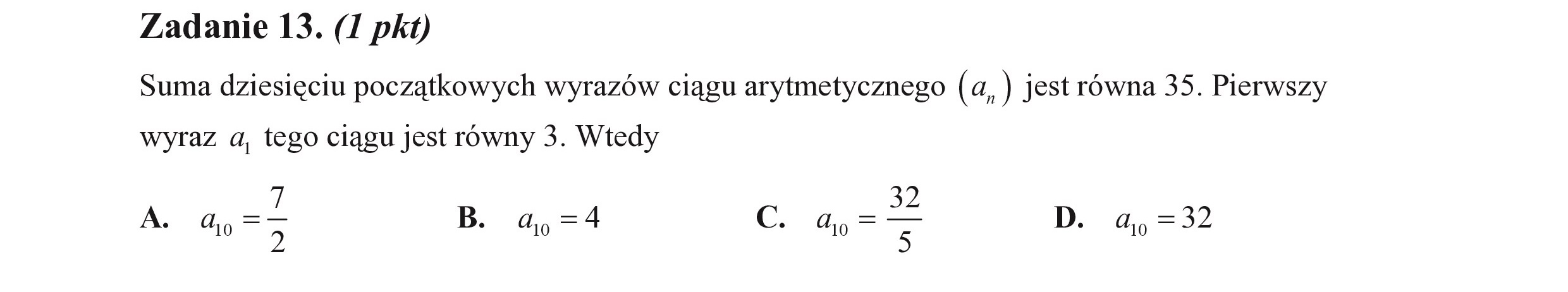
Zadanie 13. (I pkt) Suma dziesięciu początkowych wyrazów ciągu arytmetycznego (a, ) jest równa 35. Pierwszy wyraz a, tego ciągu jest równy 3. Wtedy A. a, ac B. a„,=4 Cc. a,=— D. a,=32


Zadanie 14. (I pkt) n Ciąg geometryczny (a, ) określony jest wzorem a, = "4 dla n>1. Iloraz tego ciągu jest równy A. -3 B. — a|w

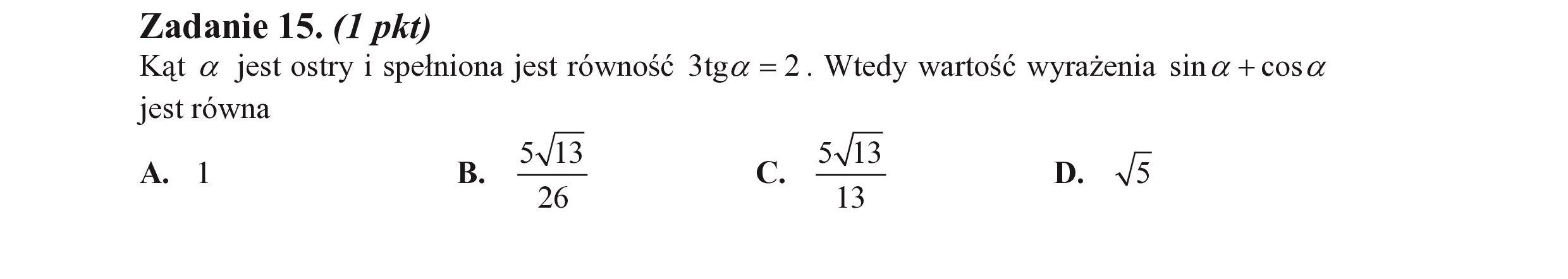
Zadanie 15. (I pkt) Kąt a jest ostry i spełniona jest równość J3tga =2. Wtedy wartość wyrażenia Sina + cosa WE SIENIE 5. 6 26 13 jest równa A. I B.


Zadanie 16. (7 pkt) Promień okręgu opisanego na trójkącie równobocznym jest równy 8. Wysokość tego trójkąta jest równa A. 4/3 B. 843 c. 12 D. 6


Zadanie 17. (I pkt) Punkty 4, B i C leżą na okręgu o środku O (zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy AOB ma miarę (pa) A. 60 B. 100? c. 120? D. 140?


Zadanie 18. (I pkt) Odcinki BC i DE są równoległe i |4E | =4, odcinka AB. Długość odcinka BC jest równa DE | = 3 (zobacz rysunek). Punkt D jest środkiem C


Zadanie 19. (I pkt) Dane są równania czterech prostych: Prostopadłe są proste A. lin B. Jim C. kin D. kim


Zadanie 20. (I pkt) Punkt P=(—1,0) leży na okręgu o promieniu 3. Równanie tego okręgu może mieć postać A. (x+I)+y7=9 B. »x*+(y-N2) =3 C. (x+1) +(y+3) =9 D. (x+1) +y)=3


Zadanie 21. (I pkt) Punkty 4=(13,-12) i C=(15,8) są przeciwległymi wierzchołkami kwadratu ABCD. Przekątne tego kwadratu przecinają się w punkcie A. S=(2,-20) B. S=f(14,10) C. S=(14,-2) D. S=(28,-4)


Zadanie 22. (I pkt) Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 4, jest równe A. 2567 B. D. 247


Zadanie 23. (I pkt) Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa Bls/ż, Objętość graniastosłupa jest równa A. 27 B. 2743 C. 243 D. 24343

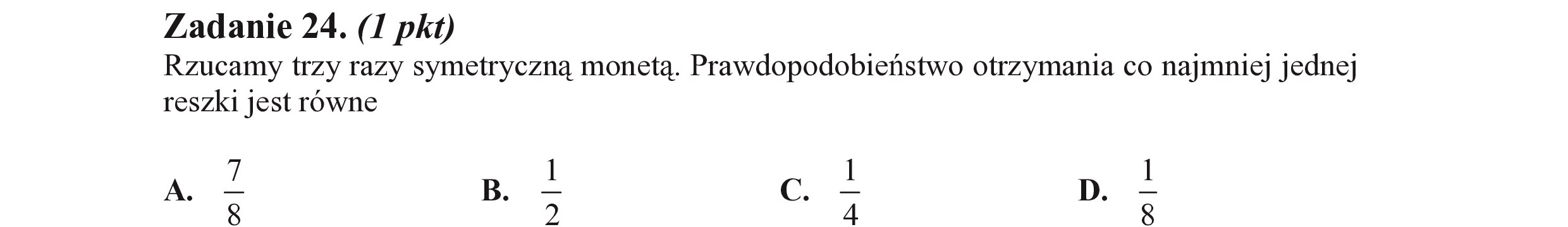
Zadanie 24. (I pkt) Rzucamy trzy razy symetryczną monetą. Prawdopodobieństwo otrzymania co najmniej jednej reszki jest równe A. Ej B. G 8 00 | — . e 7 4


Zadanie 25. (I pkt) Srednia arytmetyczna liczb: x, 13, 7, 5, 5, 3, 2, 11 jest równa 7. Mediana tego zestawu liczb jest równa A. 6 B. 7 Cc. 10 D. 5


Zadanie 26. (2 pkt) Rozwiąż nierówność —x —5x+14<0.


Zadanie 27. (2 pkt) Rozwiąż równanie x —6x —1lx+66=0.

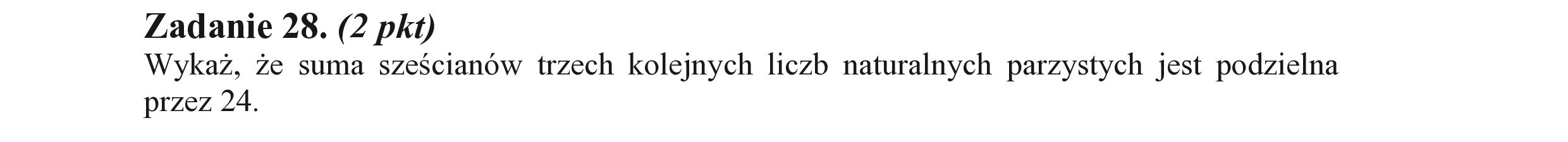
Zadanie 28. (2 pkt) Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych parzystych jest podzielna przez 24.

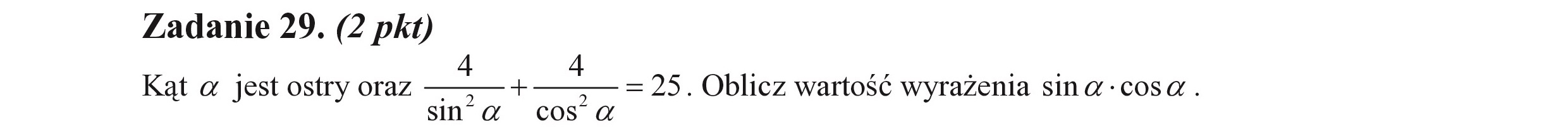
Zadanie 29. (2 pkt) . 4 Kąt a jest ostry oraz + sina cos a = 25. Oblicz wartość wyrażenia sina :cosa.


Zadanie 30. (2 pkt) Dany jest trójkąt ABC, w którym |AC|>|BC|. Na bokach AC i BC tego trójkąta obrano odpowiednio takie punkty D 1 £, że zachodzi równość |CP| = |CE | . Proste AB i DE przecinają się w punkcie F (zobacz rysunek). Wykaż, że |«BAC| = |<ABC|- 2-|<AFD|. E

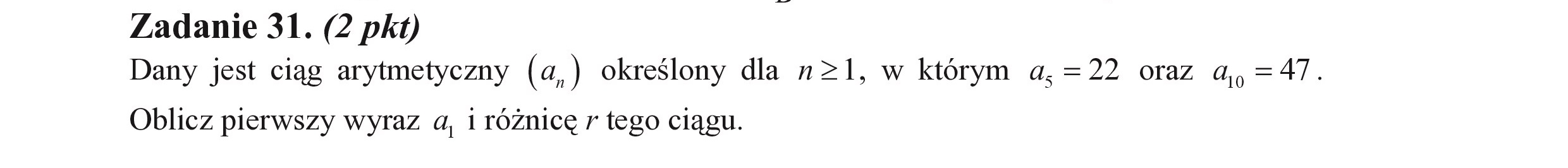
Zadanie 31. (2 pkt) Dany jest ciąg arytmetyczny (a,) określony dla n>l, w którym a, =22 oraz a,=47. Oblicz pierwszy wyraz a, i różnicę r tego ciągu.


Zadanie 32. (5 pkt) Miasta A i B są odległe o 450 km. Pani Danuta pokonała tę trasę swym samochodem w czasie o 75 minut dłuższym niż pani Lidia. Wartość średniej prędkości, z jaką jechała pani Danuta na całej trasie, była o 18 km/h mniejsza od wartości średniej prędkości, z jaką jechała pani Lidia. Oblicz średnie wartości: « prędkości, z jaką pani Danuta jechała z A do B. . prędkości, z jaką pani Lidia jechała z A do B.


Zadanie 33. (4 pkt) Podstawą ostrosłupa prawidłowego jest kwadrat. Wysokość Ściany bocznej tego ostrosłupa jest równa 22, a tangens kąta nachylenia Ściany bocznej ostrosłupa do płaszczyzny jego . - , . podstawy jest równy SD . Oblicz objętość tego ostrosłupa.


Zadanie 34. (4 pkt) Zbiór M tworzą wszystkie liczby naturalne dwucyfrowe, w zapisie których występują dwie różne cyfry spośród: 1, 2, 3, 4, 5. Ze zbioru M losujemy jedną liczbę, przy czym każda liczba z tego zbioru może być wylosowana ztym samym prawdopodobieństwem. Oblicz prawdopodobieństwo, że wylosujemy liczbę większą od 20, w której cyfra dziesiątek jest mniejsza od cyfry jedności.






























