MATEMATYKA 2014 MAJ MATURA PODSTAWOWA
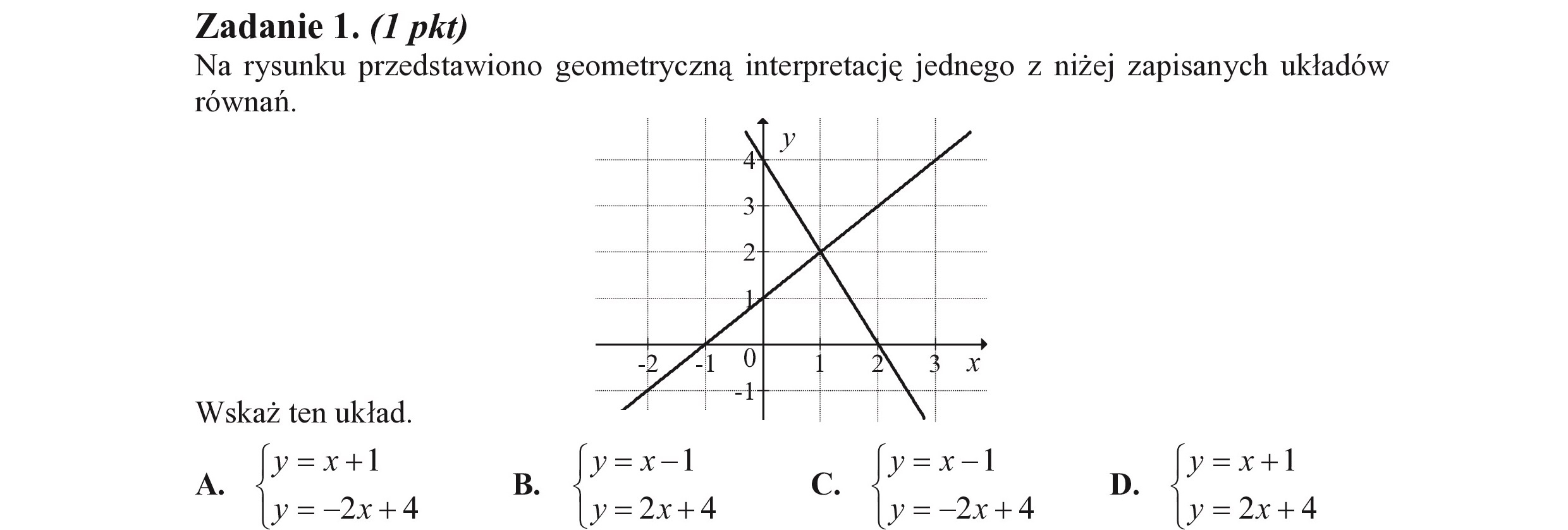
Zadanie 1. (I pkt) Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań. Wskaż ten układ. y=x+1 y=x+l B. G D. y=—2x+4 y=2x+4 y=—2x+4 y=2x+4

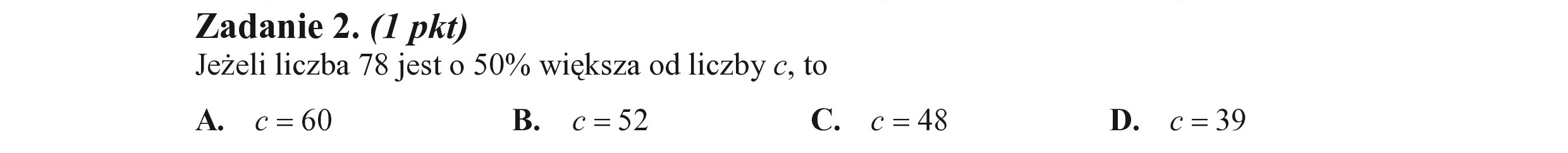
Zadanie 2. (I pkt) Jeżeli liczba 78 jest o 50% większa od liczby c, to A. c=60 B. c=$52 c. c=48


Zadanie 3. (I pia) Wartość wyrażenia —=— Au 2 2 WACT jest równa B. -213 C. 243


Zadanie 4.(1 pkt) Suma log;16+1 jest równa A. 3 B. E 2 CG. log;17 wW| 4

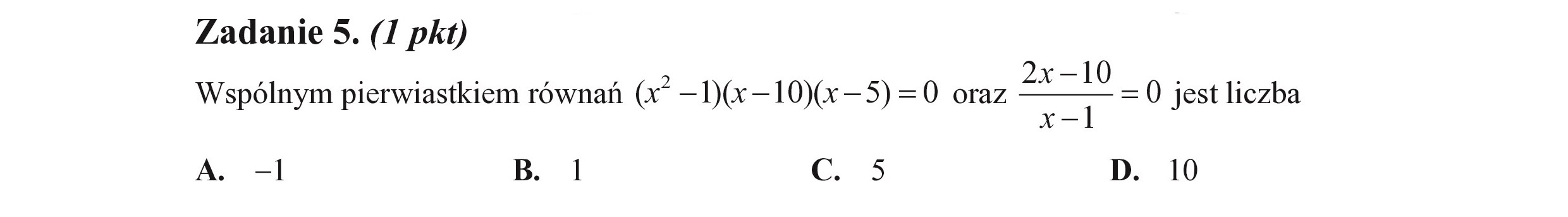
Zadanie 5. (I pkt) Wspólnym pierwiastkiem równań (x —1)(x—10)(x—5)=0 oraz =() jest liczba A. -1 B. | c. 5 D. I0


Zadanie 6. (I pkt) Funkcja liniowa /(x) = (m” —4)x +2 jest malejąca, gdy A. m e (-2,2) B. m e(—2,2) c. m e(—0,—2) D. me(2,+0)

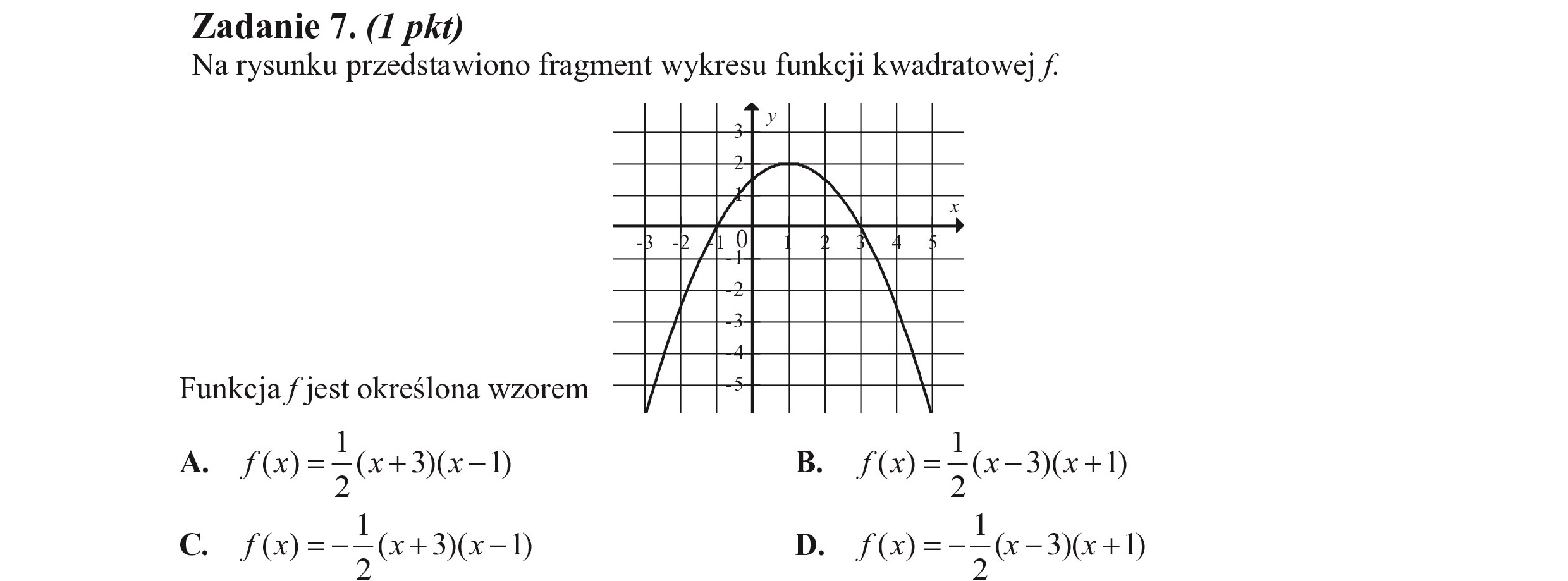
Zadanie 7. (I pkt) Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f. Funkcja f jest określona wzorem A. f(x)= 0+30-1) c. f(x)= --6+30-1) B. /(x)= 0 -3)(x +1) D. f(x)= 50-340)


Zadanie 8. (I pkt) Punkt C=(0,2) jest wierzchołkiem trapezu ABCD, którego podstawa AB jest zawarta w prostej o równaniu y = 2x —4. Wskaż równanie prostej zawierającej podstawę CD. „ A. y=x+2 B. y=-2x+2 c. p=-jx+2 D. y=2x+2

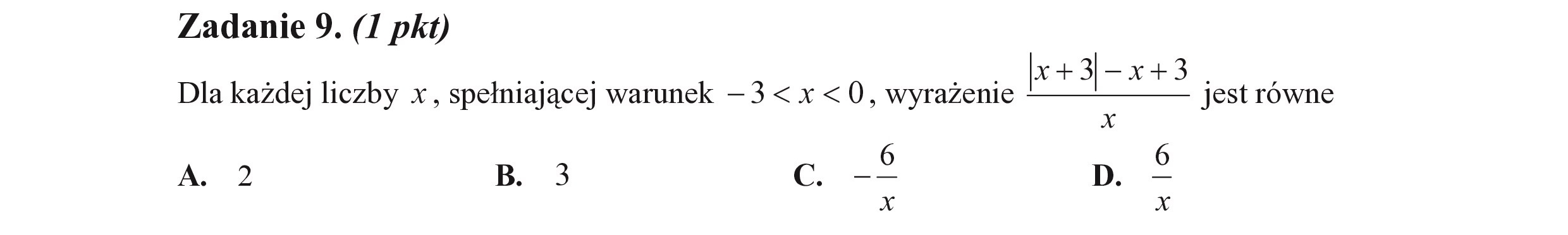
Zadanie 9. (I pkt) x+3|-x+3 Dla każdej liczby x, spełniającej warunek — 3 < x < 0, wyrażenie k+3-x+3 jest równe 4 A. 2 B. 3 GG == D. x x

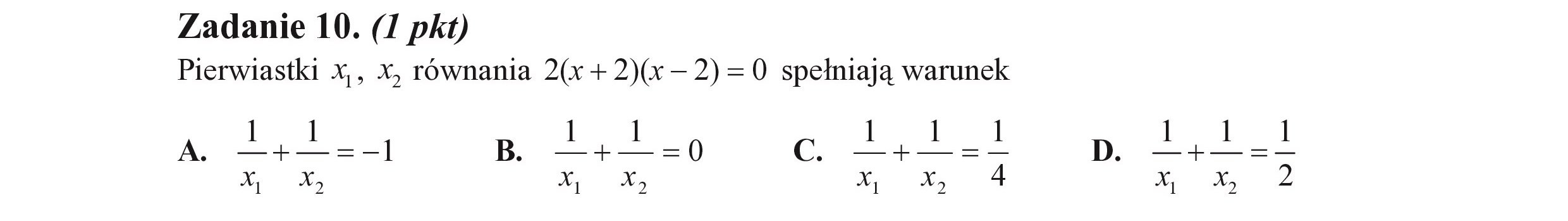
Zadanie 10. (I pkt) Pierwiastki X,, x, równania 2(x + 2)(x — 2)=0 spełniają warunek A e B =0 0. = 4 ż %, żę 4%


Zadanie 11. (I pkt) Liczby 2,-1,—4 są trzema początkowymi wyrazami ciągu arytmetycznego (a,), określonego dla liczb naturalnych n > 1. Wzór ogólny tego ciągu ma postać A. a, =-3n+5 B. a,=n-3 C. a,=-—n+3 D. a, =3n—5


Zadanie 12. (I pkt) Jeżeli trójkąty ABC i A'B'C'są podobne, a ich pola są, odpowiednio, równe 25cm” ' ' i 50 cm”, to skala podobieństwa jest równa c. 42 D. A. 2 B. o|G 1 2


Zadanie 13. (I pkt) Liczby. x—2, 6, 12, w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba x jest równa A. 0 B. 2 GB D. 5

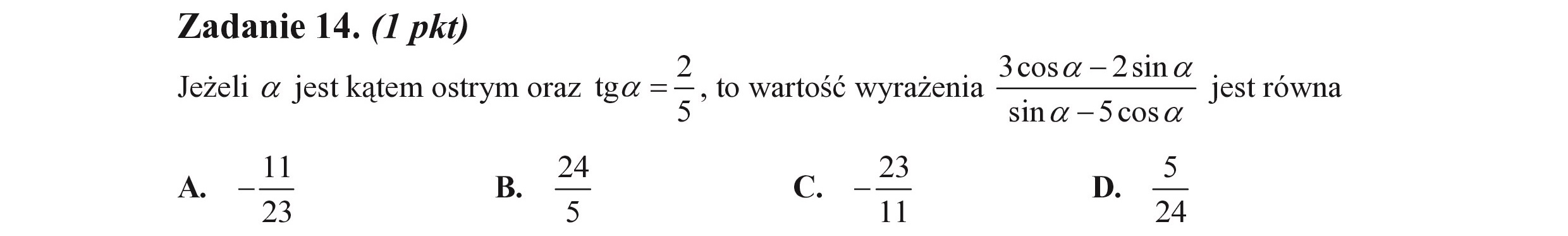
Zadanie 14. (I pkt) OB — 6 > = ._. 3cosa—2sina . ą Jeżeli a jest kątem ostrym oraz tga =—, to wartość wyrażenia ——————- jest równa 5 sin 2a —5COsa z B. Ź G D. — 23 5 11 24


Zadanie 15. (I pkt) Liczba punktów wspólnych okręgu o równaniu (x+2) +(v-3) =4 z osiami układu współrzędnych jest równa A. 0 B. I c. 2 D. 4


Zadanie 16. (I pkt) Wysokość trapezu równoramiennego o kącie ostrym 60” i ramieniu długości 24/3 jest równa A. 43 B. 3 G 243 D. 2


Zadanie 17. (I pkt) , 4 . , Kąt środkowy oparty na łuku, którego długość jest równa 5 długości okręgu, ma miarę A. 1602 B. 802 C. 40? D. 20?

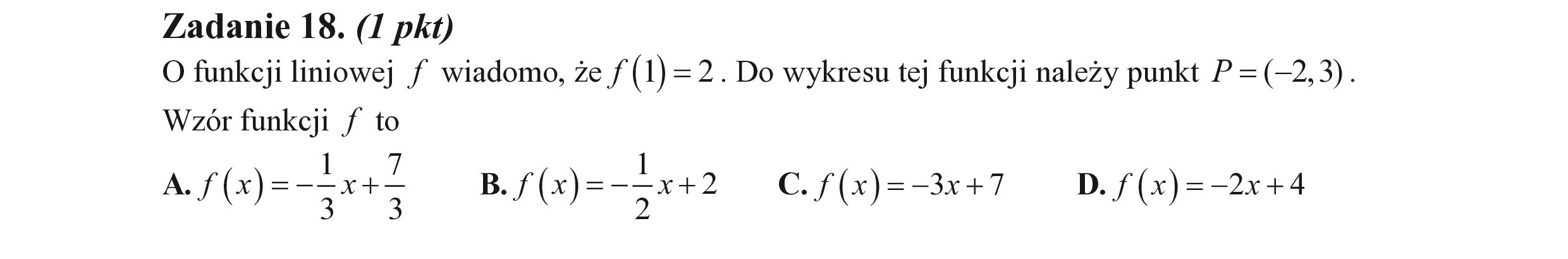
Zadanie 18. (I pkt) O funkcji liniowej / wiadomo, że f (1) =2. Do wykresu tej funkcji należy punkt P =(—2,3). Wzór funkcji / to 7 A.f(x)="ża+> B./(1)=->x+2 C. f(x)=-3x+7 D. f(x)=—2x+4

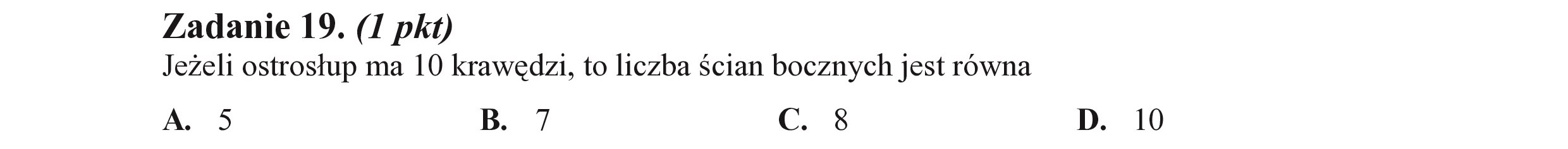
Zadanie 19. (I pkt) Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa A. 5 B. 7 C. 8 10


Zadanie 20. (I pkt) Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest A. sześć razy dłuższa od wysokości walca. B. trzy razy dłuższa od wysokości walca. C. dwa razy dłuższa od wysokości walca. D równa wysokości walca.


Zadanie 21. (I pkt) : l , : Liczba jest równa (4729 +4256 +2) ke B. — 225 Ik.

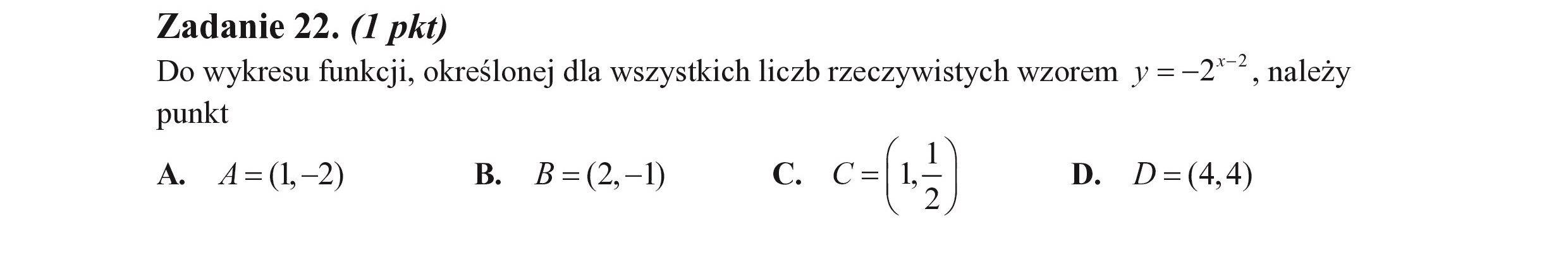
Zadanie 22. (I pkt) Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem y =—2"*, należy punkt A. A=(1-2) B. B=(2-1 C. c-(15) D. D=(4,4)


Zadanie 23. (I pkt) Jeżeli A jest zdarzeniem losowym, a 4' -zdarzeniem przeciwnym do zdarzenia A oraz zachodzi równość P(4)=2:P(A'), to A. PA=Z 2 P(A)== c. PLA=> D. PLA)=Ę

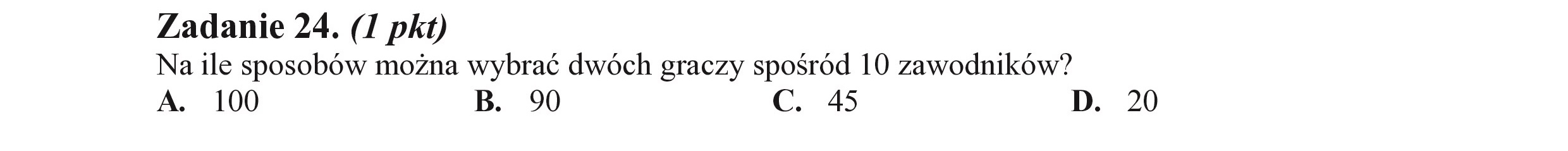
Zadanie 24. (I pkt) Na ile sposobów można wybrać dwóch graczy spośród 10 zawodników? A. 100 B. 90 C. 45 D. 20

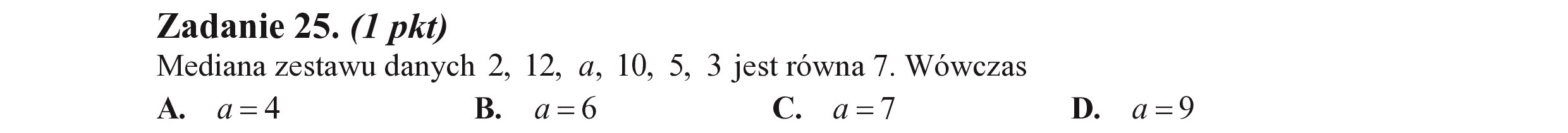
Zadanie 25. (I pkt) Mediana zestawu danych 2, 12, a, 10, 5, 3 jest równa 7. Wówczas A. a=4 B. a=6 C. a=7


Zadanie 26. (2 pkt) Wykresem funkcji kwadratowej /(x)= 2x +bx+ce jest parabola, której wierzchołkiem jest punkt W =(4,0). Oblicz wartości współczynników b i c.

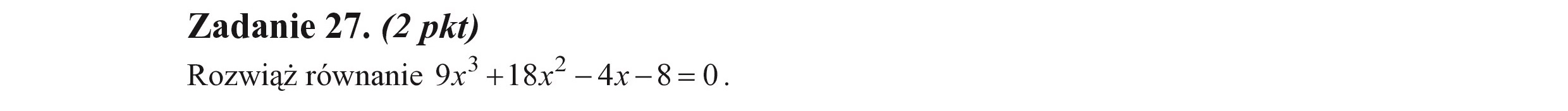
Zadanie 27. (2 pkt) Rozwiąż równanie 0x” +18x* —4x-8=0.


Zadanie 28. (2 pkt) Udowodnij, że każda liczba całkowita k, która przy dzieleniu przez 7 daje resztę 2, ma tę własność, że reszta z dzielenia liczby 3k* przez 7 jest równa 5.

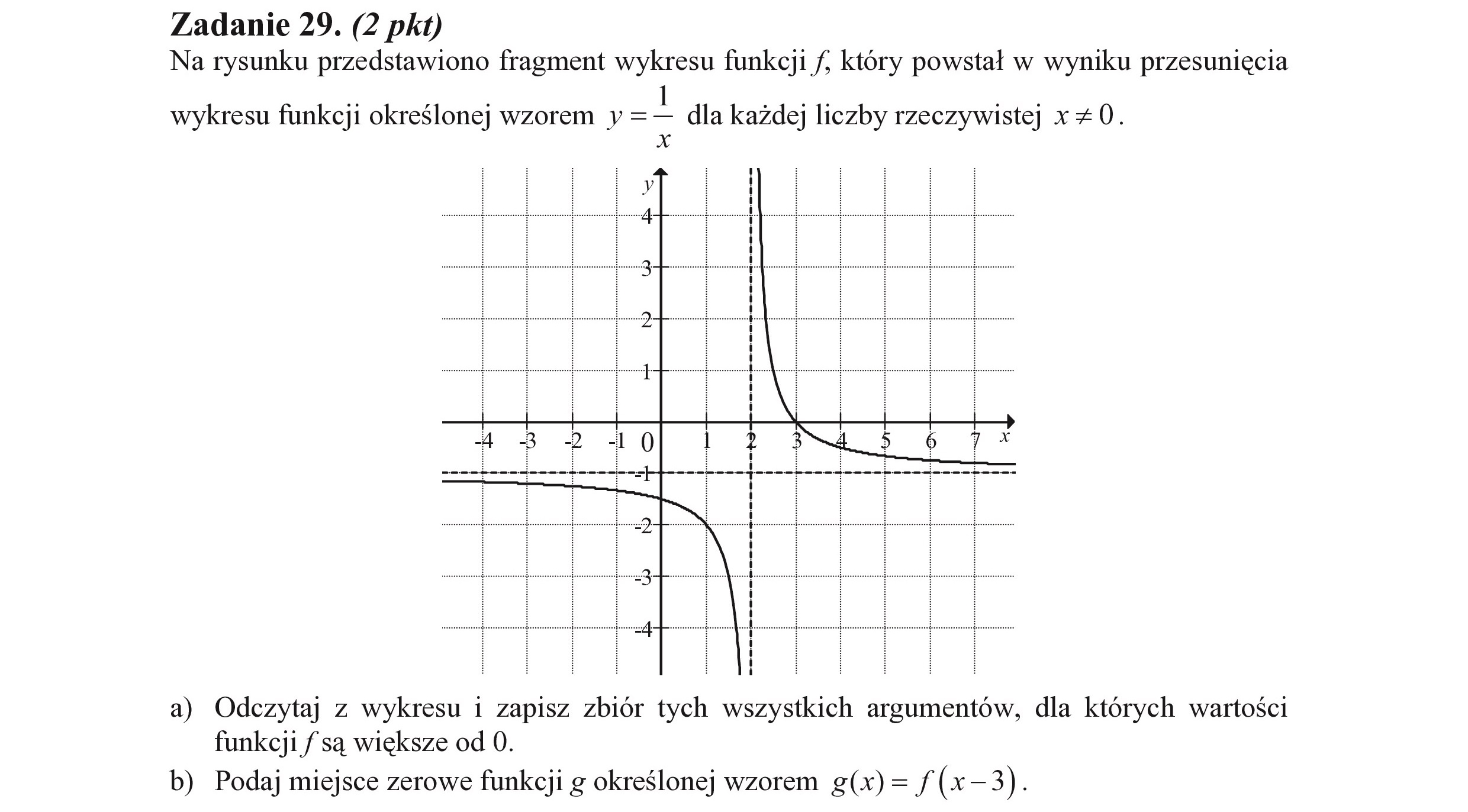
Zadanie 29. (2 pkt) Na rysunku przedstawiono fragment wykresu funkcji /, który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem y =— dla każdej liczby rzeczywistej x +0. X funkcji /f są większe od 0. b) Podaj miejsce zerowe funkcji g określonej wzorem g(x) = /(x-3).


Zadanie 30. (2 pkt) Ze zbioru liczb (1. 2, 3, 4,5, 6, 7, 8) losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia A, polegającego na wylosowaniu liczb, z których pierwsza jest większa od drugiej o 4 lub 6.

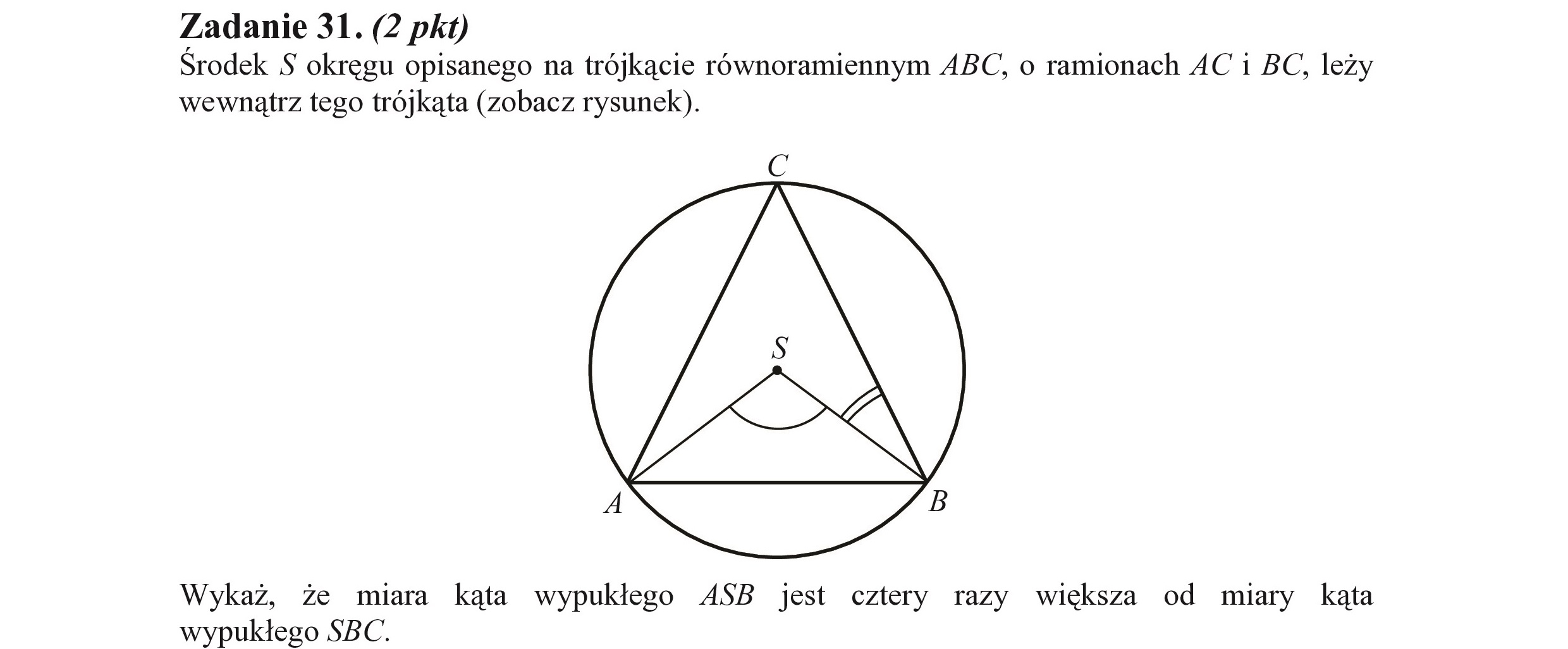
Zadanie 31. (2 pkt) Srodek $ okręgu opisanego na trójkącie równoramiennym ABC, o ramionach AC i BC, leży wewnątrz tego trójkąta (zobacz rysunek). G A B Wykaż, że miara kąta wypukłego ASB jest cztery razy większa od miary kąta wypukłego SBC.


Zadanie 32. (4 pkt) Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1: 2:3. Oblicz długość przekątnej tego prostopadłościanu.


Zadanie 33. (5 pkt) Turysta zwiedzał zamek stojący na wzgórzu. Droga łącząca parking z zamkiem ma długość 2,1 km. Łączny czas wędrówki turysty z parkingu do zamku i z powrotem, nie licząc czasu poświęconego na zwiedzanie, był równy 1 godzinę i 4 minuty. Oblicz, z jaką średnią prędkością turysta wchodził na wzgórze, jeżeli prędkość ta była o 1 ra mniejsza od średniej prędkości, z jaką schodził ze wzgórza.

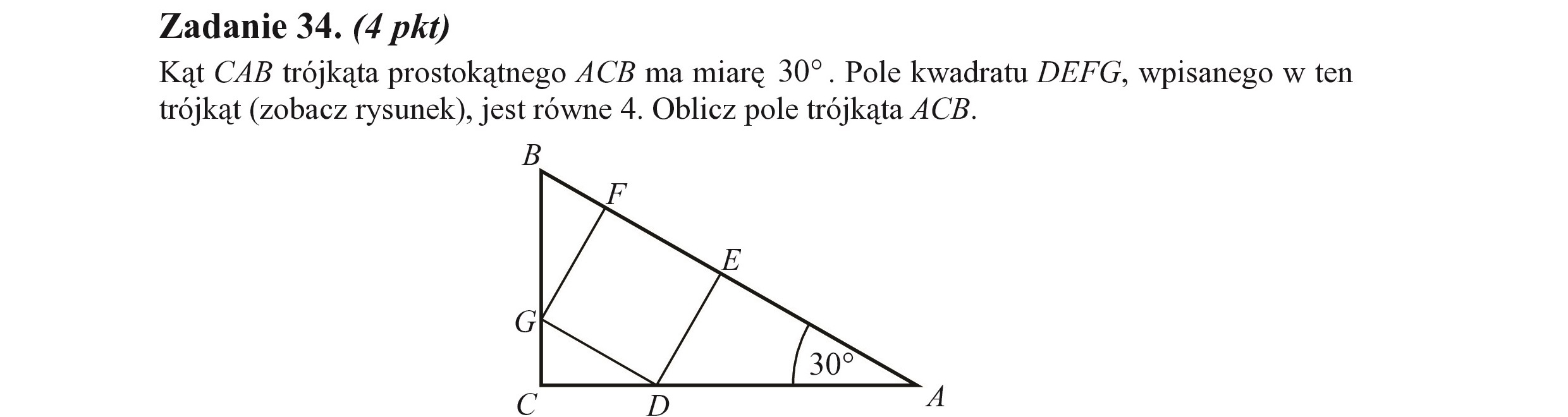
Zadanie 34. (4 pkt) Kąt CAB trójkąta prostokątnego ACB ma miarę 30”. Pole kwadratu DEFG, wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta ACB.

MATEMATYKA 2014 MAJ MATURA PODSTAWOWA

Zadanie 1. (I pkt) Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań. Wskaż ten układ. y=x+1 y=x+l B. G D. y=—2x+4 y=2x+4 y=—2x+4 y=2x+4

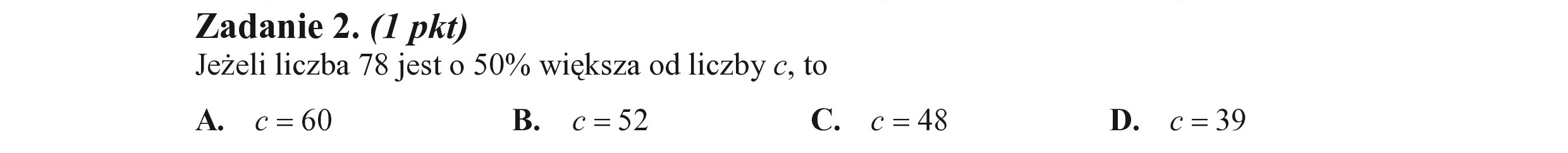
Zadanie 2. (I pkt) Jeżeli liczba 78 jest o 50% większa od liczby c, to A. c=60 B. c=$52 c. c=48


Zadanie 3. (I pia) Wartość wyrażenia —=— Au 2 2 WACT jest równa B. -213 C. 243


Zadanie 4.(1 pkt) Suma log;16+1 jest równa A. 3 B. E 2 CG. log;17 wW| 4

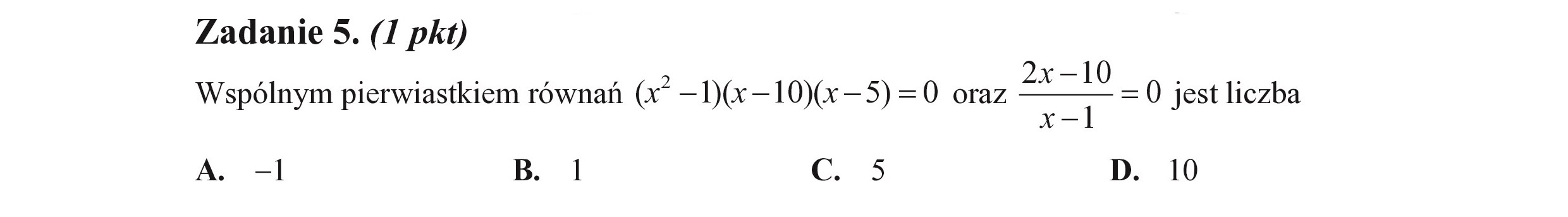
Zadanie 5. (I pkt) Wspólnym pierwiastkiem równań (x —1)(x—10)(x—5)=0 oraz =() jest liczba A. -1 B. | c. 5 D. I0


Zadanie 6. (I pkt) Funkcja liniowa /(x) = (m” —4)x +2 jest malejąca, gdy A. m e (-2,2) B. m e(—2,2) c. m e(—0,—2) D. me(2,+0)


Zadanie 7. (I pkt) Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f. Funkcja f jest określona wzorem A. f(x)= 0+30-1) c. f(x)= --6+30-1) B. /(x)= 0 -3)(x +1) D. f(x)= 50-340)


Zadanie 8. (I pkt) Punkt C=(0,2) jest wierzchołkiem trapezu ABCD, którego podstawa AB jest zawarta w prostej o równaniu y = 2x —4. Wskaż równanie prostej zawierającej podstawę CD. „ A. y=x+2 B. y=-2x+2 c. p=-jx+2 D. y=2x+2

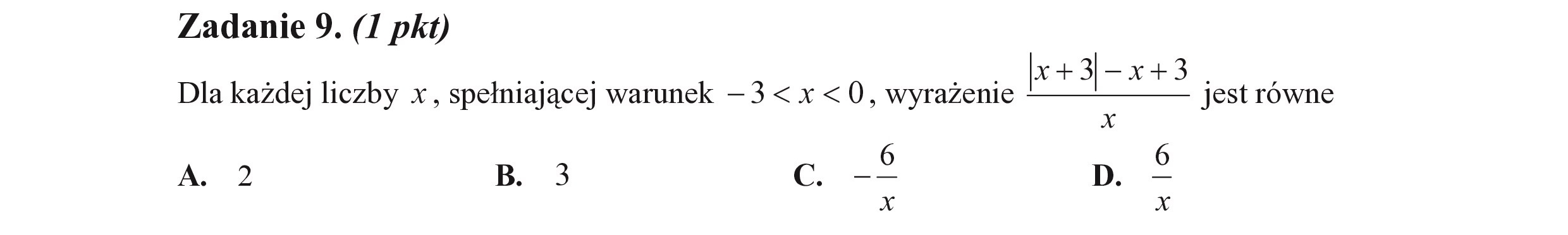
Zadanie 9. (I pkt) x+3|-x+3 Dla każdej liczby x, spełniającej warunek — 3 < x < 0, wyrażenie k+3-x+3 jest równe 4 A. 2 B. 3 GG == D. x x

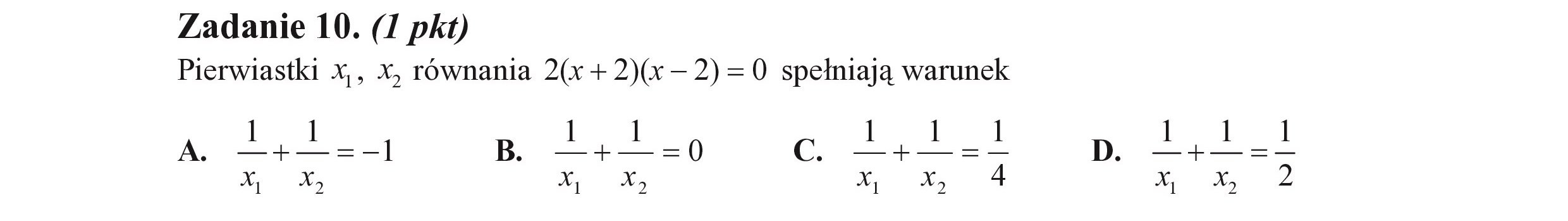
Zadanie 10. (I pkt) Pierwiastki X,, x, równania 2(x + 2)(x — 2)=0 spełniają warunek A e B =0 0. = 4 ż %, żę 4%


Zadanie 11. (I pkt) Liczby 2,-1,—4 są trzema początkowymi wyrazami ciągu arytmetycznego (a,), określonego dla liczb naturalnych n > 1. Wzór ogólny tego ciągu ma postać A. a, =-3n+5 B. a,=n-3 C. a,=-—n+3 D. a, =3n—5


Zadanie 12. (I pkt) Jeżeli trójkąty ABC i A'B'C'są podobne, a ich pola są, odpowiednio, równe 25cm” ' ' i 50 cm”, to skala podobieństwa jest równa c. 42 D. A. 2 B. o|G 1 2


Zadanie 13. (I pkt) Liczby. x—2, 6, 12, w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba x jest równa A. 0 B. 2 GB D. 5

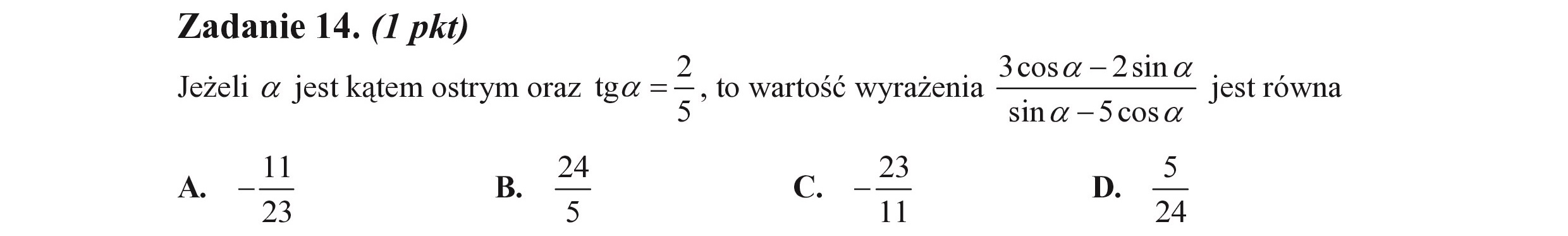
Zadanie 14. (I pkt) OB — 6 > = ._. 3cosa—2sina . ą Jeżeli a jest kątem ostrym oraz tga =—, to wartość wyrażenia ——————- jest równa 5 sin 2a —5COsa z B. Ź G D. — 23 5 11 24


Zadanie 15. (I pkt) Liczba punktów wspólnych okręgu o równaniu (x+2) +(v-3) =4 z osiami układu współrzędnych jest równa A. 0 B. I c. 2 D. 4


Zadanie 16. (I pkt) Wysokość trapezu równoramiennego o kącie ostrym 60” i ramieniu długości 24/3 jest równa A. 43 B. 3 G 243 D. 2


Zadanie 17. (I pkt) , 4 . , Kąt środkowy oparty na łuku, którego długość jest równa 5 długości okręgu, ma miarę A. 1602 B. 802 C. 40? D. 20?

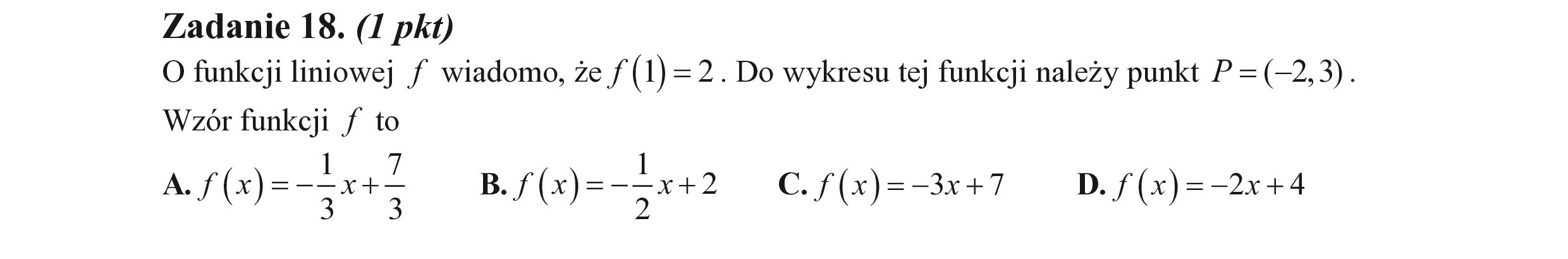
Zadanie 18. (I pkt) O funkcji liniowej / wiadomo, że f (1) =2. Do wykresu tej funkcji należy punkt P =(—2,3). Wzór funkcji / to 7 A.f(x)="ża+> B./(1)=->x+2 C. f(x)=-3x+7 D. f(x)=—2x+4

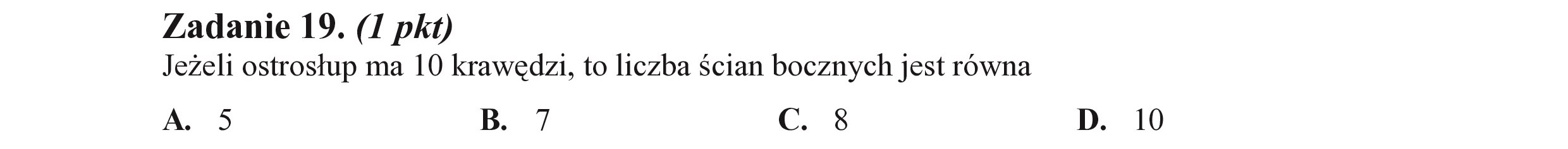
Zadanie 19. (I pkt) Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa A. 5 B. 7 C. 8 10


Zadanie 20. (I pkt) Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest A. sześć razy dłuższa od wysokości walca. B. trzy razy dłuższa od wysokości walca. C. dwa razy dłuższa od wysokości walca. D równa wysokości walca.


Zadanie 21. (I pkt) : l , : Liczba jest równa (4729 +4256 +2) ke B. — 225 Ik.

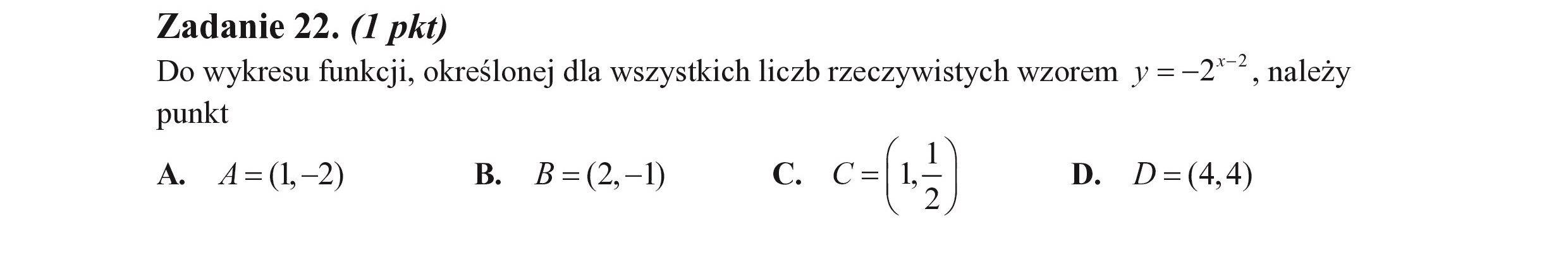
Zadanie 22. (I pkt) Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem y =—2"*, należy punkt A. A=(1-2) B. B=(2-1 C. c-(15) D. D=(4,4)


Zadanie 23. (I pkt) Jeżeli A jest zdarzeniem losowym, a 4' -zdarzeniem przeciwnym do zdarzenia A oraz zachodzi równość P(4)=2:P(A'), to A. PA=Z 2 P(A)== c. PLA=> D. PLA)=Ę

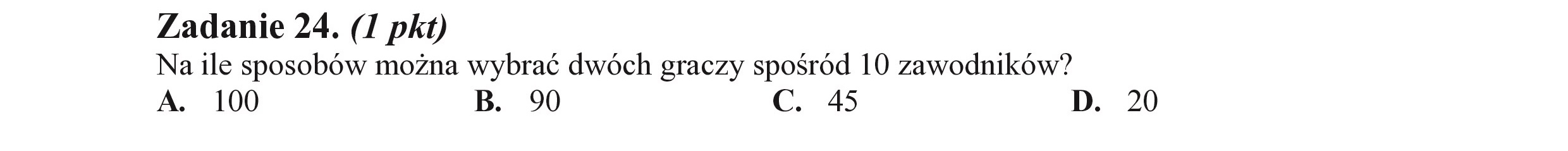
Zadanie 24. (I pkt) Na ile sposobów można wybrać dwóch graczy spośród 10 zawodników? A. 100 B. 90 C. 45 D. 20

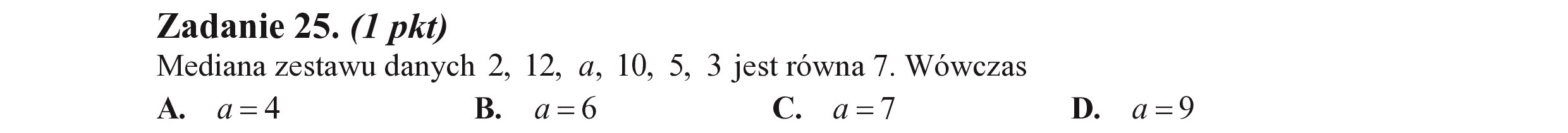
Zadanie 25. (I pkt) Mediana zestawu danych 2, 12, a, 10, 5, 3 jest równa 7. Wówczas A. a=4 B. a=6 C. a=7


Zadanie 26. (2 pkt) Wykresem funkcji kwadratowej /(x)= 2x +bx+ce jest parabola, której wierzchołkiem jest punkt W =(4,0). Oblicz wartości współczynników b i c.

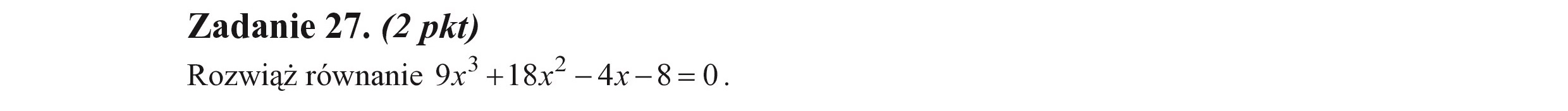
Zadanie 27. (2 pkt) Rozwiąż równanie 0x” +18x* —4x-8=0.


Zadanie 28. (2 pkt) Udowodnij, że każda liczba całkowita k, która przy dzieleniu przez 7 daje resztę 2, ma tę własność, że reszta z dzielenia liczby 3k* przez 7 jest równa 5.


Zadanie 29. (2 pkt) Na rysunku przedstawiono fragment wykresu funkcji /, który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem y =— dla każdej liczby rzeczywistej x +0. X funkcji /f są większe od 0. b) Podaj miejsce zerowe funkcji g określonej wzorem g(x) = /(x-3).


Zadanie 30. (2 pkt) Ze zbioru liczb (1. 2, 3, 4,5, 6, 7, 8) losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia A, polegającego na wylosowaniu liczb, z których pierwsza jest większa od drugiej o 4 lub 6.


Zadanie 31. (2 pkt) Srodek $ okręgu opisanego na trójkącie równoramiennym ABC, o ramionach AC i BC, leży wewnątrz tego trójkąta (zobacz rysunek). G A B Wykaż, że miara kąta wypukłego ASB jest cztery razy większa od miary kąta wypukłego SBC.


Zadanie 32. (4 pkt) Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1: 2:3. Oblicz długość przekątnej tego prostopadłościanu.


Zadanie 33. (5 pkt) Turysta zwiedzał zamek stojący na wzgórzu. Droga łącząca parking z zamkiem ma długość 2,1 km. Łączny czas wędrówki turysty z parkingu do zamku i z powrotem, nie licząc czasu poświęconego na zwiedzanie, był równy 1 godzinę i 4 minuty. Oblicz, z jaką średnią prędkością turysta wchodził na wzgórze, jeżeli prędkość ta była o 1 ra mniejsza od średniej prędkości, z jaką schodził ze wzgórza.


Zadanie 34. (4 pkt) Kąt CAB trójkąta prostokątnego ACB ma miarę 30”. Pole kwadratu DEFG, wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta ACB.






























