MATEMATYKA 2013 MAJ MATURA PODSTAWOWA
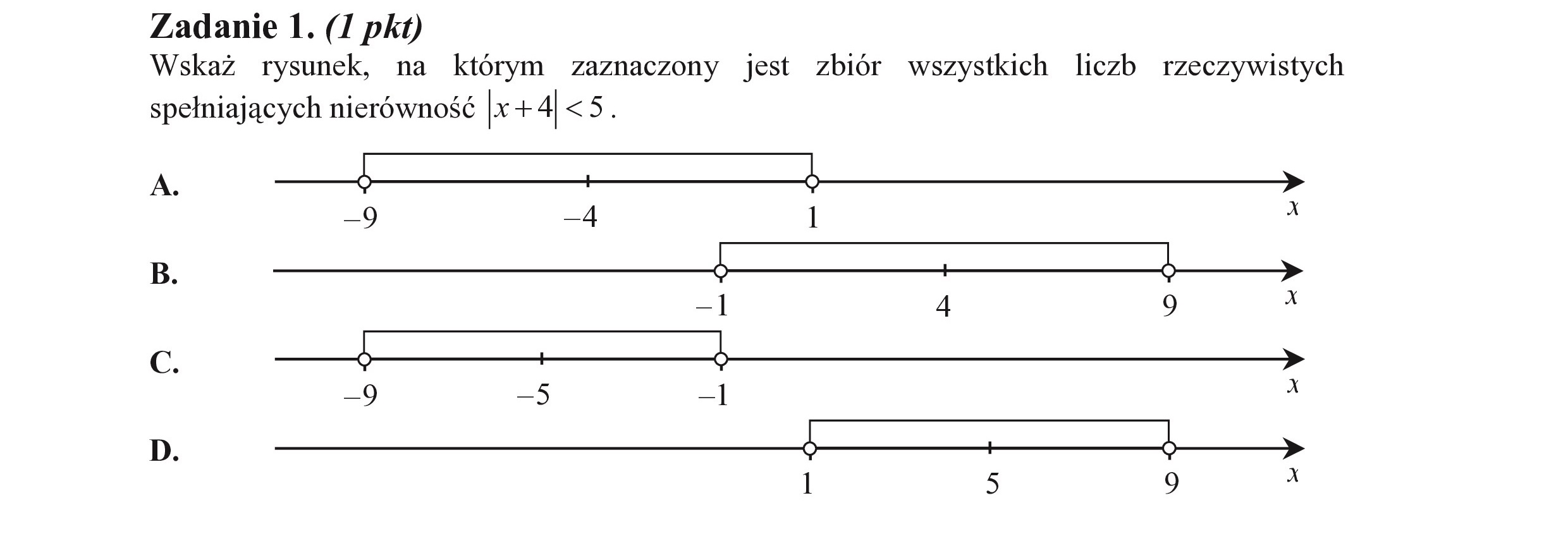
Zadanie 1. (I pkt) Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność | + 4 <5. A. ZZ WNNNNNNEYNNNNNNNNNE KAEZZEEEEEEEEE | -9 —4 1 A B. | |2)2ŁLŹŻ,_„_.JĄ_ 4 ||| 4 y -| 4 9 8 rę NA 45 GF -9 -5 —1 A


Zadanie 2. (I pkt) Liczby a i b są dodatnie oraz 12% liczby a jest równe 15% liczby b. Stąd wynika, że a jest równe A. 103% liczby b B. 125% liczby b Cc. 150% liczbyb D. 153% liczbyb

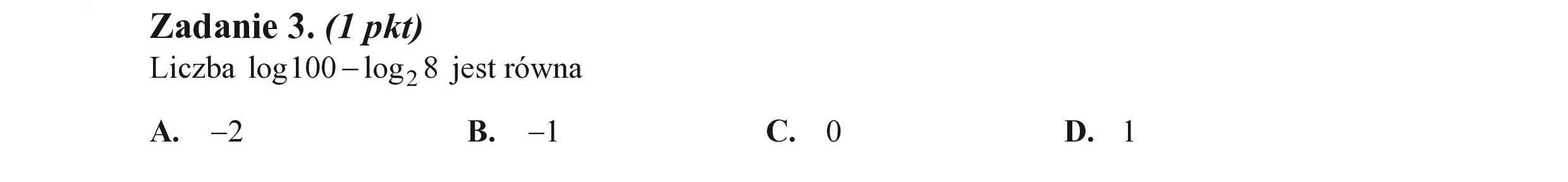
Zadanie 3. (I pkt) Liczba log100 —log> 8 jest równa A. 2 B. -1

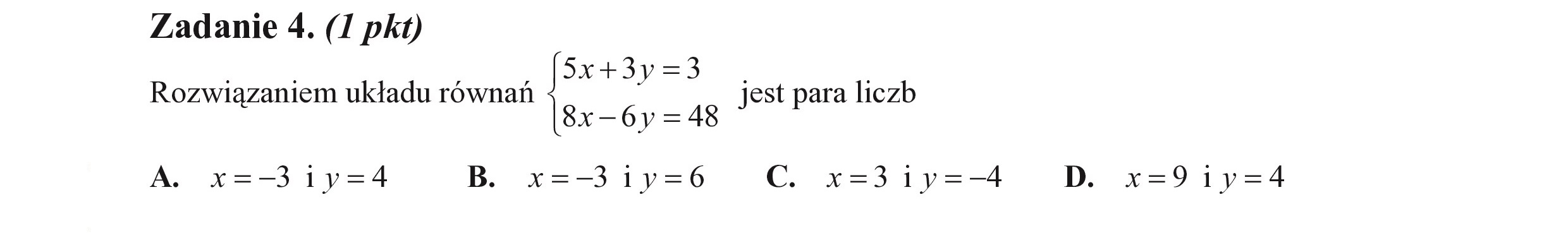
Zadanie 4. (I pkt) . . „, |5Sx+Zy=3 |. . Rozwiązaniem układu równań jest para liczb 8x —6y = 48 A. x=-31y=4 B. x=-3iy=6 C. x=3iy=— D. x=9iy=4

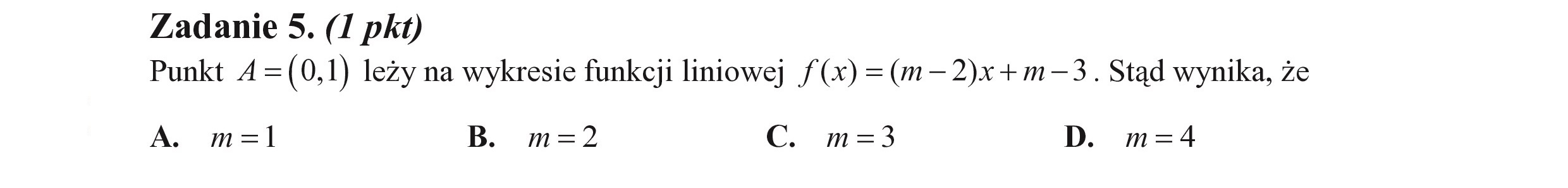
Zadanie 5. (I pkt) Punkt A= (0, 1) leży na wykresie funkcji liniowej /(x) =(m—2)x+m—3. Stąd wynika, że A. m=l B. m=2 c. m=3 D. m=4

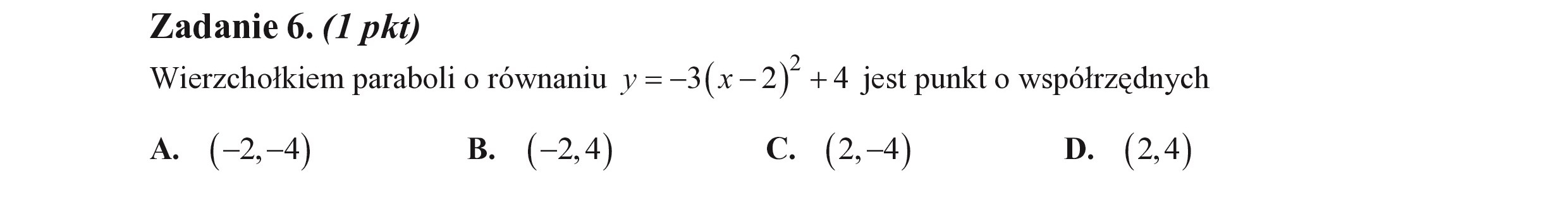
Zadanie 6. (1 pkt) Wierzchołkiem paraboli o równaniu y= -3(x-— 2) +4 jest punkt o współrzędnych A. (-2,—4) B. (-2,4) c. (2,4) b. (2,4)

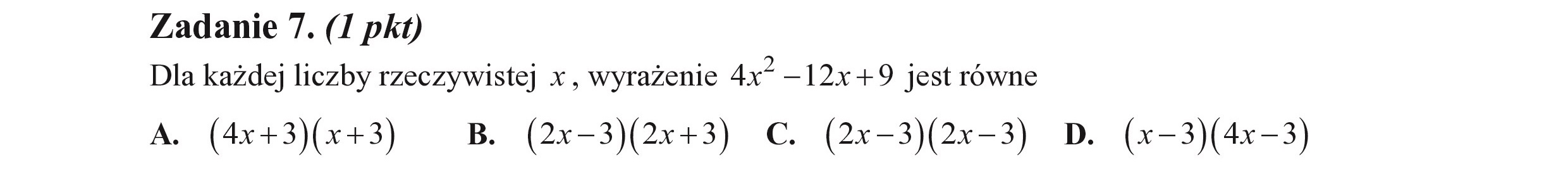
Zadanie 7. (I pkt) Dla każdej liczby rzeczywistej x , wyrażenie 4x* —12x+9 jest równe A. (4x +3)(x+3) B. (2x-3)(2x+3) c (2x-3)(2x-3) D. (x-3)(4x—3)


Zadanie 8. (I pkt) Prosta o równaniu SEP | jest prostopadła do prostej o równaniu p=-ża—1. Stąd m wynika, że A. m=—-3 B. UE c. n=> D. m=3


Zadanie 9. (I pkt) Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej y=ax+b. Jakie znaki mają współczynniki aib? A. a<0ib<0 B. a<0ib>0 C.a>01b<0 D. a>0i1b>0

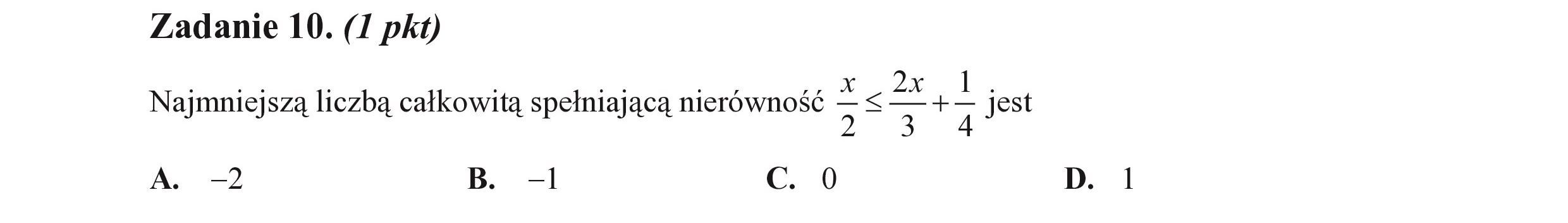
Zadanie 10. (I pkt) Najmniejszą liczbą całkowitą spełniającą nierówność A < > + 4 jest A. 2 B. -1 c. 0

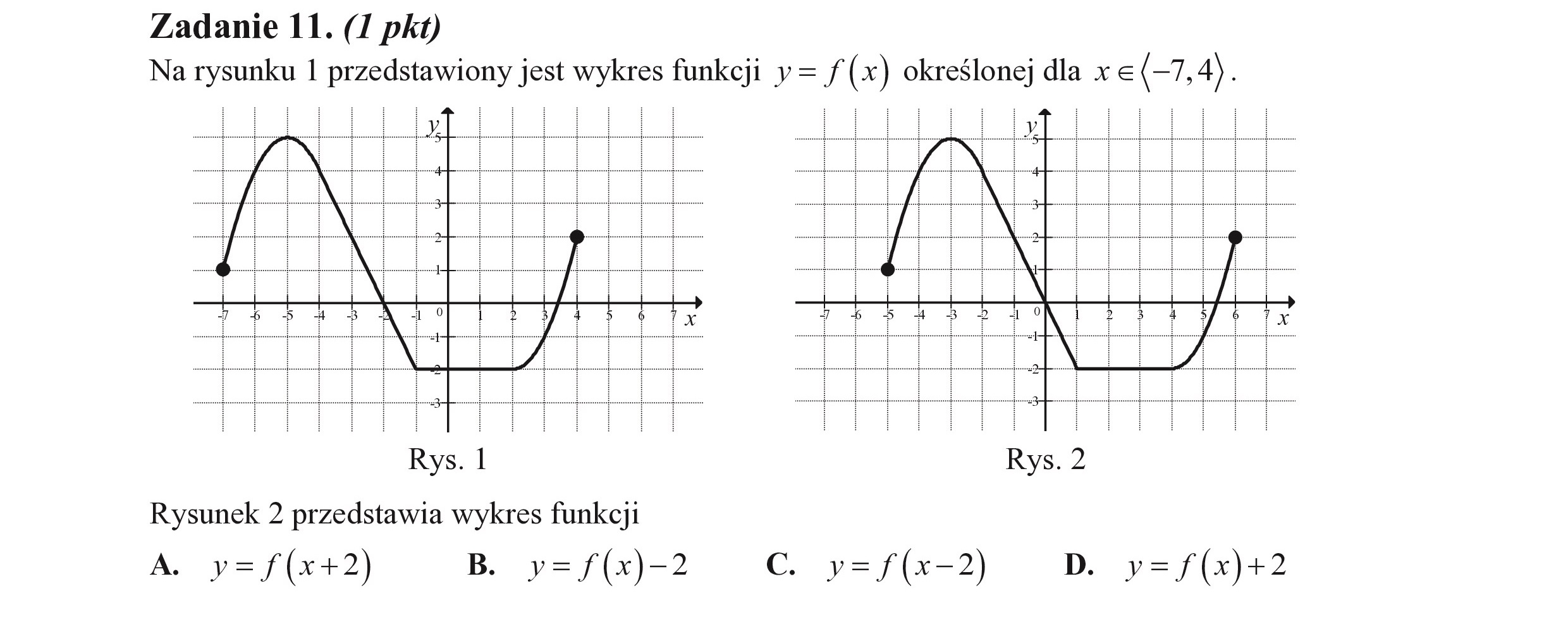
Zadanie 11. (I pkt) Na rysunku I przedstawiony jest wykres funkcji y= f (x) określonej dla x € (-7, 4). Rysunek 2 przedstawia wykres funkcji A. y=f(x+2) B. y=/f(x)-2 C. y=f(x-2) D. y=/f(x)+2

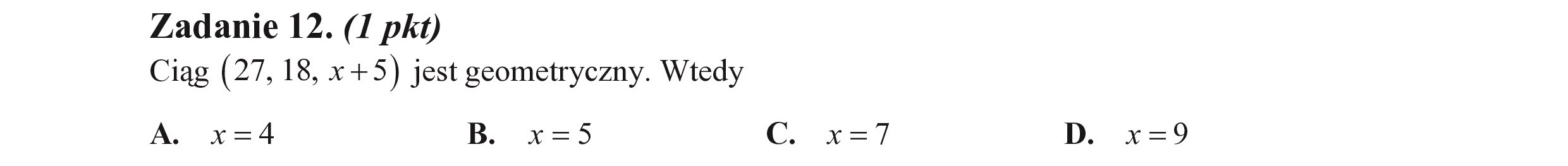
Zadanie 12. (I pkt) Ciąg (27, 18, x+5) jest geometryczny. Wtedy A. x=4 B. X=5

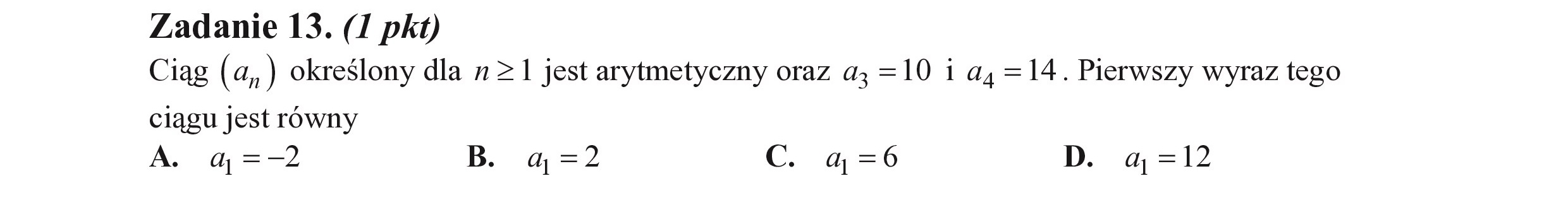
Zadanie 13. (I pkt) Ciąg (a„) określony dla n>1 jest arytmetyczny oraz a; =10 i a, =14. Pierwszy wyraz tego ciągu jest równy A. q=-—2 B. qaq=2 C. q=6 D. a=12

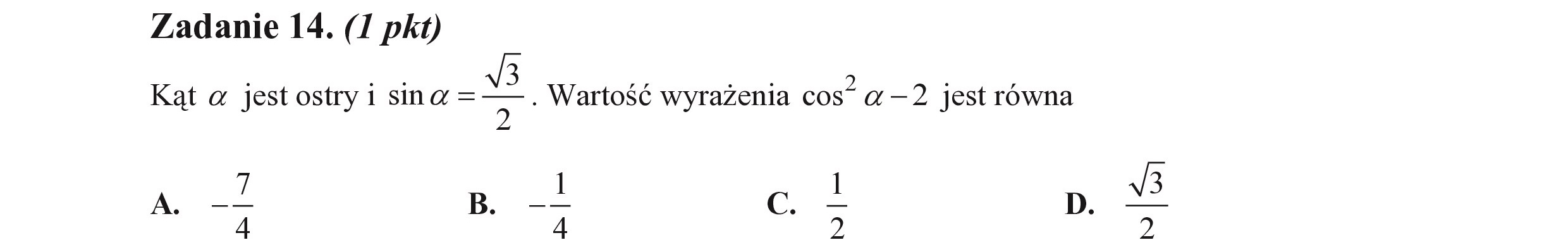
Zadanie 14. (I pkt) Kąt a jest ostry i sina = sh „. Wartość wyrażenia cos” a —2 jest równa A. - p. —L c. | p. 4 4 3 2

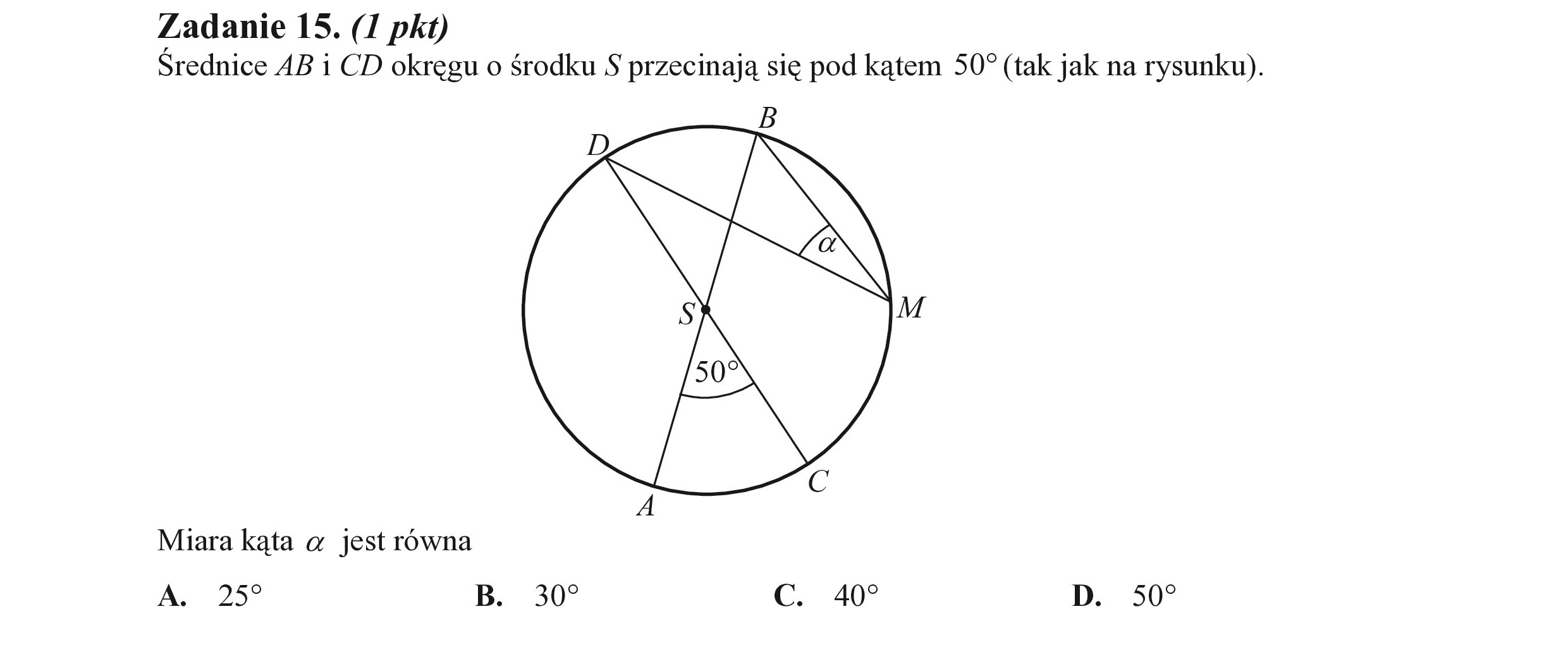
Zadanie 15. (I pkt) Srednice AB i CD okręgu o środku S$ przecinają się pod kątem 50” (tak jak na rysunku). Miara kąta a jest równa A. 259 B. 307 Cc. 40? D. 50?

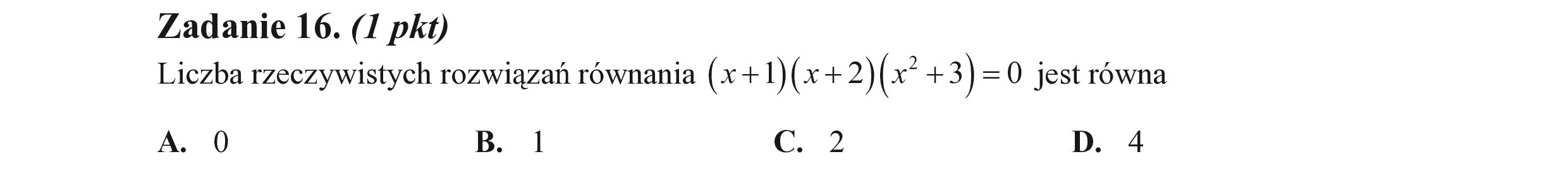
Zadanie 16. (I pkt) Liczba rzeczywistych rozwiązań równania (x ł 1)(x ł 2)( ł 3) =() jest równa A. 0 B. I c. 2 D. 4


Zadanie 17. (I pkt) Punkty A= (-1,2) 1 A= (5, —2) są dwoma sąsiednimi wierzchołkami rombu ABCD. Obwód tego rombu jest równy A. A13 B. 13 C. 676 D. 8413


Zadanie 18. (I pkt) Punkt S=(—4, 7) jest środkiem odcinka PQ, gdzie Q=(17, 12). Zatem punkt P ma współrzędne A. P=(2,-25) ' B. P=(38,17) C. P=(-25, 2) D. P=(—-12, 4)


Zadanie 19. (I pkt) Odległość między środkami okręgów o równaniach (x+ 1 +( y-2) =9 oraz x +y =10 jest równa A. 45 B. 10-3 C. 3 D. 5


Zadanie 20. (I pkt) Liczba wszystkich krawędzi graniastosłupa jest o 10 większa od liczby wszystkich jego Ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest A. czworokąt B. pięciokąt C. sześciokąt D. dziesięciokąt


Zadanie 21. (I pkt) Pole powierzchni bocznej stożka o wysokości 4 i promieniu podstawy 3 jest równe A. 97 B. 12z Cc. 157 D. 167


Zadanie 22. (I pkt) Rzucamy dwa razy symetryczną sześcienną kostką do gry. Niech p oznacza prawdopodobieństwo zdarzenia, że iloczyn liczb wyrzuconych oczek jest równy 5. Wtedy l l l l A. P-%6 B. P = 18 c. P"1 D. D=5


Zadanie 23. (I pkt) V50-418 . 2 Liczba "2 jest równa A. 242 B. 2 D. 10-06


Zadanie 24. (I pkt) Mediana uporządkowanego niemalejąco zestawu sześciu liczb: 1, 2,3, x,5,8 jest równa 4. Wtedy A. x=2 B. x=3 C. x=4 D. x=5


Zadanie 25. (I pkt) Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 2843. Długość krawędzi podstawy tego graniastosłupa jest równa A. 2 B. 4 C. 8 D. 16


Zadanie 26. (2 pkt) Rozwiąż równanie x +2x —8x-16=0.


Zadanie 27. (2 pkt) Kąt a jest ostry i sina =—— . Oblicz wartość wyrażenia sin” 2 —3cos* a. 43 EJ

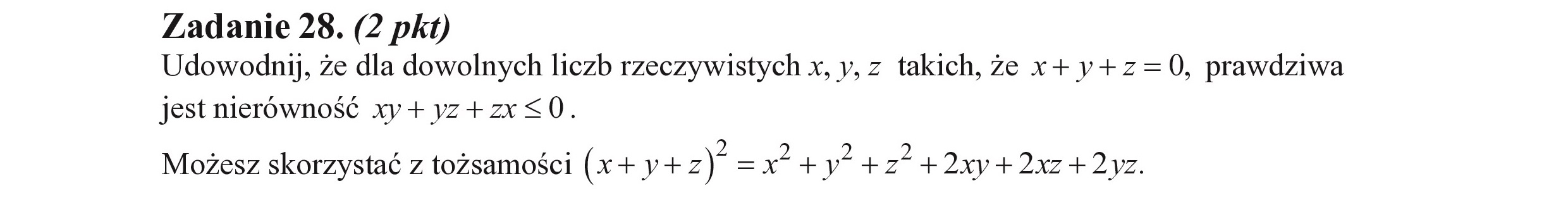
Zadanie 28. (2 pkt) Udowodnij, że dla dowolnych liczb rzeczywistych x, y, z takich, że x+y+z=0, prawdziwa jest nierówność xyv+ yz+zx<0. ME = 3 Możesz skorzystać z tożsamości (x+y+z) =x* +y” +z” +2xy+2xz +2yz. „

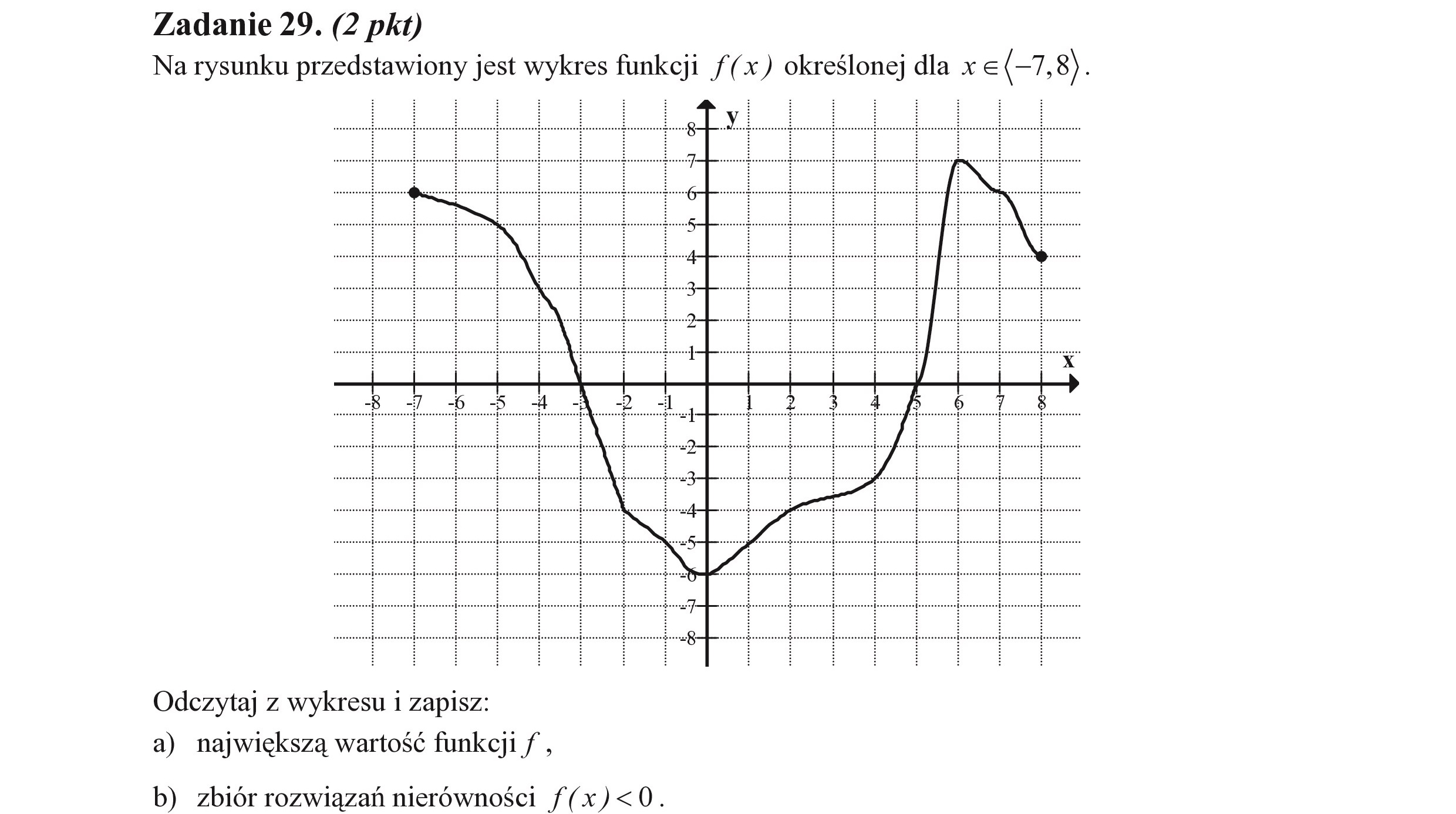
Zadanie 29. (2 pkt) Na rysunku przedstawiony jest wykres funkcji f(x) określonej dla x € (-7, 8). Odczytaj z wykresu i zapisz: a) największą wartość funkcji /, b) zbiór rozwiązań nierówności /(x)<0.


Zadanie 30. (2 pkt) Rozwiąż nierówność 2x -7x+520.


Zadanie 31. (2 pkt) Wykaż, że liczba 6" —2-6” +10-6* jest podzielna przez 17.

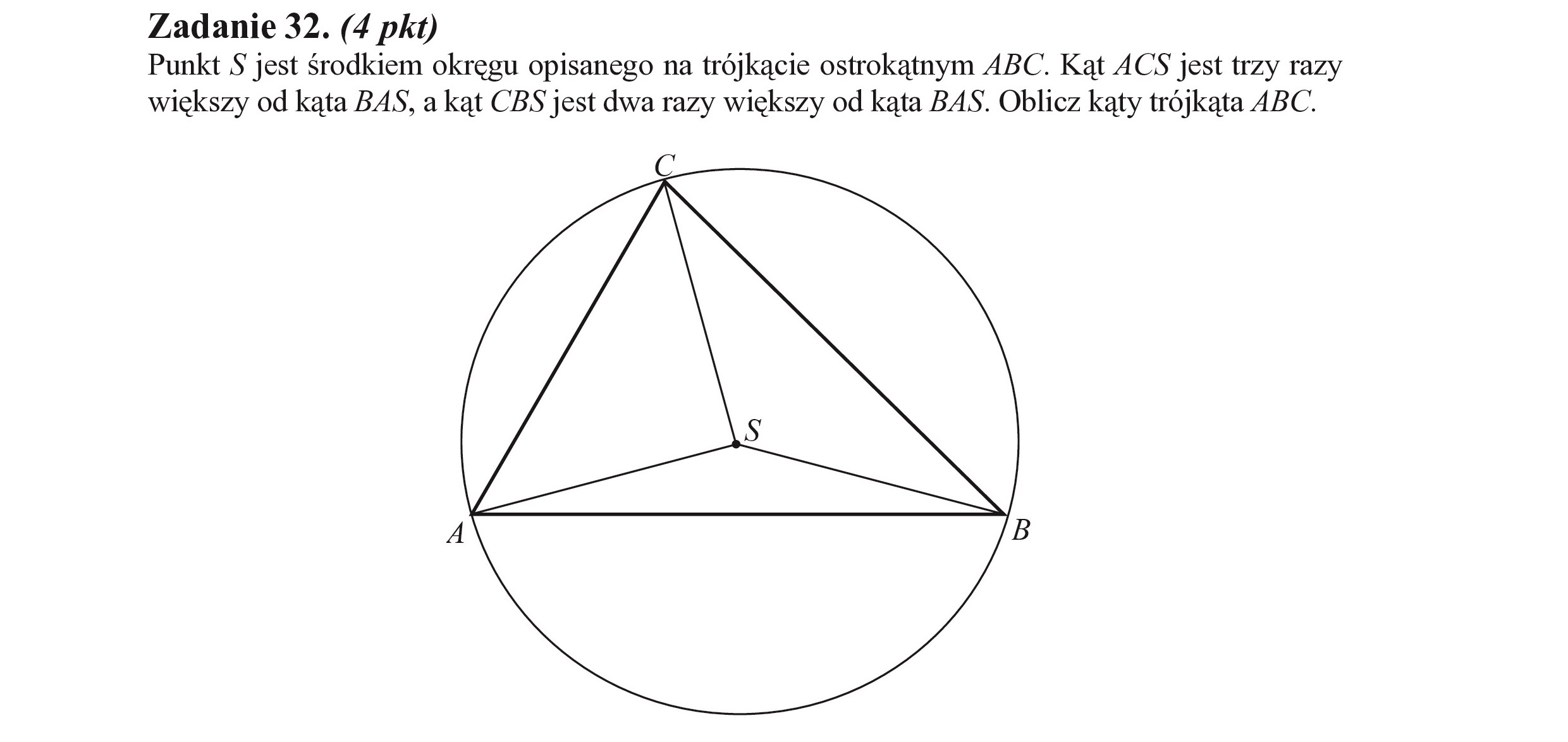
Zadanie 32. (4 pkt) Punkt S$ jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Kąt ACS jest trzy razy większy od kąta BAS, a kąt CBS jest dwa razy większy od kąta BAS. Oblicz kąty trójkąta ABC. C


Zadanie 33. (4 pkt) Pole podstawy ostrosłupa prawidłowego czworokątnego jest równe 100 cm, a jego pole powierzchni bocznej jest równe 260 cm”. Oblicz objętość tego ostrosłupa.


Zadanie 34. (5 pkt) Dwa miasta łączy linia kolejowa o długości 336 kilometrów. Pierwszy pociąg przebył tę trasę w czasie o 40 minut krótszym niż drugi pociąg. Średnia prędkość pierwszego pociągu na tej trasie była o 9 km/h większa od średniej prędkości drugiego pociągu. Oblicz średnią prędkość każdego z tych pociągów na tej trasie.

MATEMATYKA 2013 MAJ MATURA PODSTAWOWA

Zadanie 1. (I pkt) Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność | + 4 <5. A. ZZ WNNNNNNEYNNNNNNNNNE KAEZZEEEEEEEEE | -9 —4 1 A B. | |2)2ŁLŹŻ,_„_.JĄ_ 4 ||| 4 y -| 4 9 8 rę NA 45 GF -9 -5 —1 A


Zadanie 2. (I pkt) Liczby a i b są dodatnie oraz 12% liczby a jest równe 15% liczby b. Stąd wynika, że a jest równe A. 103% liczby b B. 125% liczby b Cc. 150% liczbyb D. 153% liczbyb

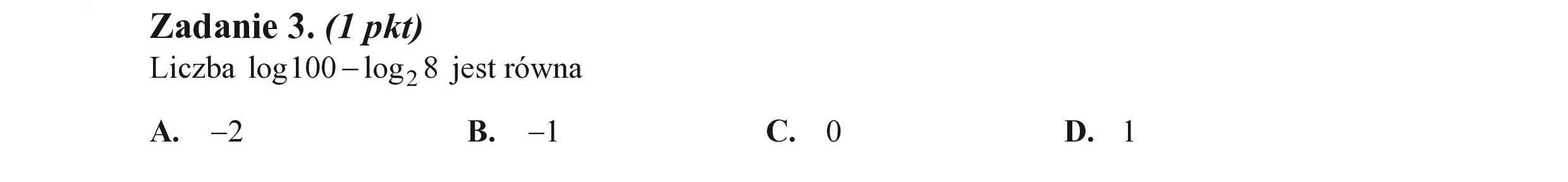
Zadanie 3. (I pkt) Liczba log100 —log> 8 jest równa A. 2 B. -1

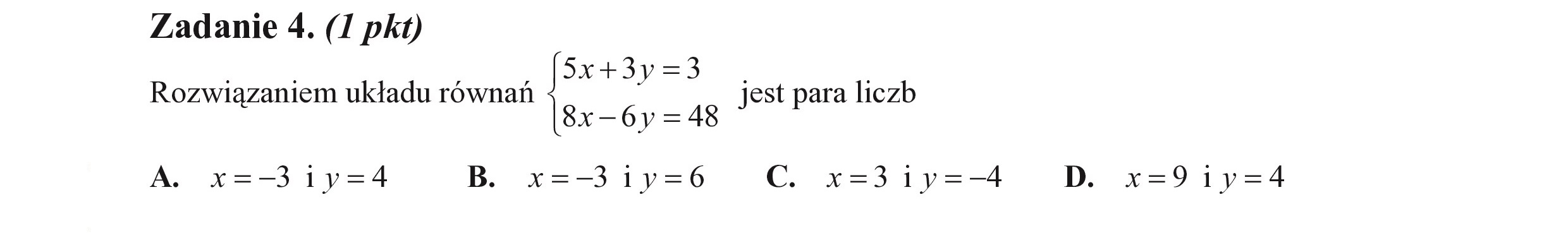
Zadanie 4. (I pkt) . . „, |5Sx+Zy=3 |. . Rozwiązaniem układu równań jest para liczb 8x —6y = 48 A. x=-31y=4 B. x=-3iy=6 C. x=3iy=— D. x=9iy=4

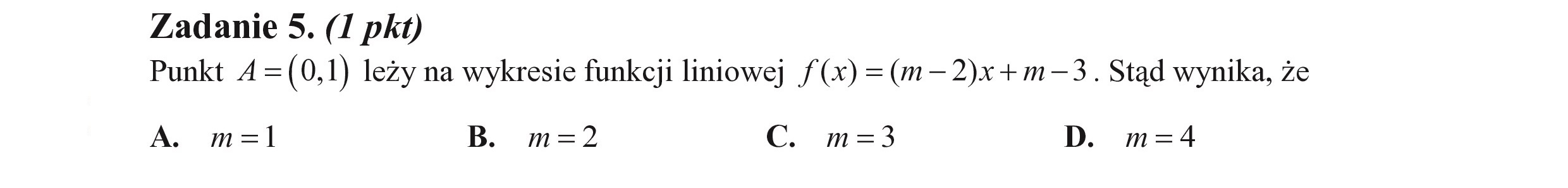
Zadanie 5. (I pkt) Punkt A= (0, 1) leży na wykresie funkcji liniowej /(x) =(m—2)x+m—3. Stąd wynika, że A. m=l B. m=2 c. m=3 D. m=4

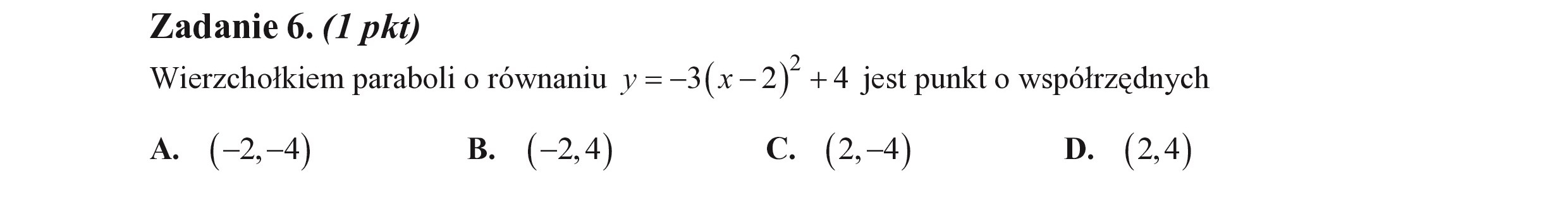
Zadanie 6. (1 pkt) Wierzchołkiem paraboli o równaniu y= -3(x-— 2) +4 jest punkt o współrzędnych A. (-2,—4) B. (-2,4) c. (2,4) b. (2,4)

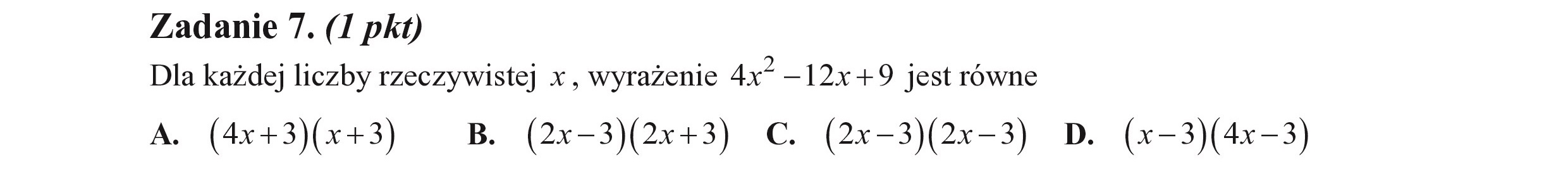
Zadanie 7. (I pkt) Dla każdej liczby rzeczywistej x , wyrażenie 4x* —12x+9 jest równe A. (4x +3)(x+3) B. (2x-3)(2x+3) c (2x-3)(2x-3) D. (x-3)(4x—3)


Zadanie 8. (I pkt) Prosta o równaniu SEP | jest prostopadła do prostej o równaniu p=-ża—1. Stąd m wynika, że A. m=—-3 B. UE c. n=> D. m=3


Zadanie 9. (I pkt) Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej y=ax+b. Jakie znaki mają współczynniki aib? A. a<0ib<0 B. a<0ib>0 C.a>01b<0 D. a>0i1b>0

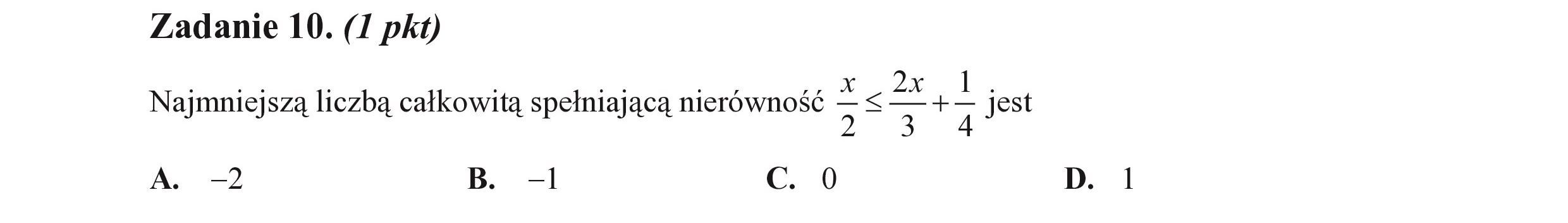
Zadanie 10. (I pkt) Najmniejszą liczbą całkowitą spełniającą nierówność A < > + 4 jest A. 2 B. -1 c. 0


Zadanie 11. (I pkt) Na rysunku I przedstawiony jest wykres funkcji y= f (x) określonej dla x € (-7, 4). Rysunek 2 przedstawia wykres funkcji A. y=f(x+2) B. y=/f(x)-2 C. y=f(x-2) D. y=/f(x)+2

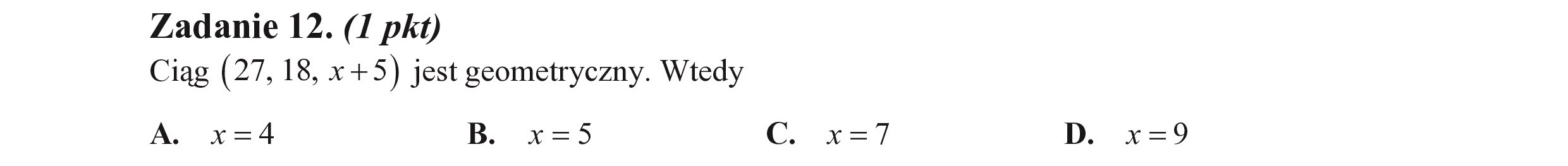
Zadanie 12. (I pkt) Ciąg (27, 18, x+5) jest geometryczny. Wtedy A. x=4 B. X=5

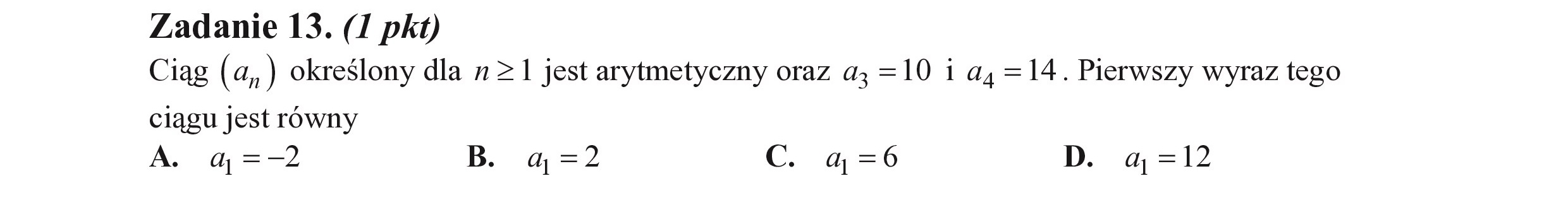
Zadanie 13. (I pkt) Ciąg (a„) określony dla n>1 jest arytmetyczny oraz a; =10 i a, =14. Pierwszy wyraz tego ciągu jest równy A. q=-—2 B. qaq=2 C. q=6 D. a=12

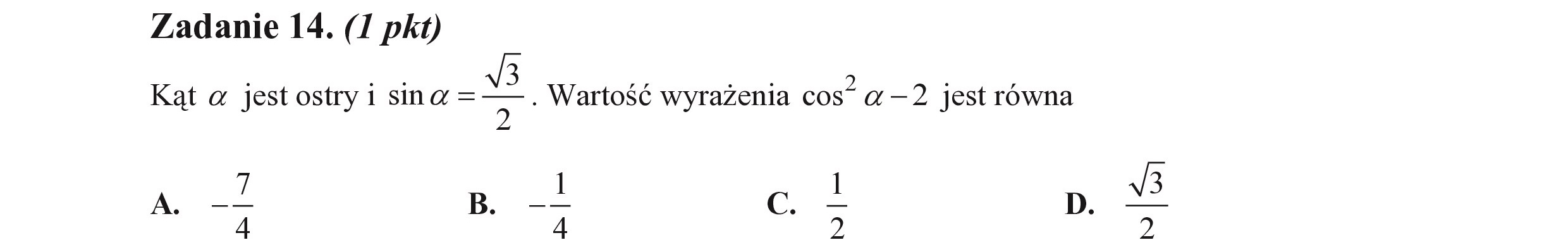
Zadanie 14. (I pkt) Kąt a jest ostry i sina = sh „. Wartość wyrażenia cos” a —2 jest równa A. - p. —L c. | p. 4 4 3 2


Zadanie 15. (I pkt) Srednice AB i CD okręgu o środku S$ przecinają się pod kątem 50” (tak jak na rysunku). Miara kąta a jest równa A. 259 B. 307 Cc. 40? D. 50?

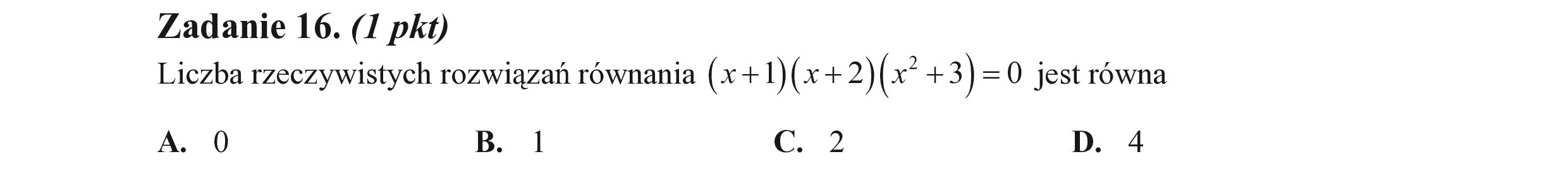
Zadanie 16. (I pkt) Liczba rzeczywistych rozwiązań równania (x ł 1)(x ł 2)( ł 3) =() jest równa A. 0 B. I c. 2 D. 4


Zadanie 17. (I pkt) Punkty A= (-1,2) 1 A= (5, —2) są dwoma sąsiednimi wierzchołkami rombu ABCD. Obwód tego rombu jest równy A. A13 B. 13 C. 676 D. 8413


Zadanie 18. (I pkt) Punkt S=(—4, 7) jest środkiem odcinka PQ, gdzie Q=(17, 12). Zatem punkt P ma współrzędne A. P=(2,-25) ' B. P=(38,17) C. P=(-25, 2) D. P=(—-12, 4)


Zadanie 19. (I pkt) Odległość między środkami okręgów o równaniach (x+ 1 +( y-2) =9 oraz x +y =10 jest równa A. 45 B. 10-3 C. 3 D. 5


Zadanie 20. (I pkt) Liczba wszystkich krawędzi graniastosłupa jest o 10 większa od liczby wszystkich jego Ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest A. czworokąt B. pięciokąt C. sześciokąt D. dziesięciokąt


Zadanie 21. (I pkt) Pole powierzchni bocznej stożka o wysokości 4 i promieniu podstawy 3 jest równe A. 97 B. 12z Cc. 157 D. 167


Zadanie 22. (I pkt) Rzucamy dwa razy symetryczną sześcienną kostką do gry. Niech p oznacza prawdopodobieństwo zdarzenia, że iloczyn liczb wyrzuconych oczek jest równy 5. Wtedy l l l l A. P-%6 B. P = 18 c. P"1 D. D=5


Zadanie 23. (I pkt) V50-418 . 2 Liczba "2 jest równa A. 242 B. 2 D. 10-06


Zadanie 24. (I pkt) Mediana uporządkowanego niemalejąco zestawu sześciu liczb: 1, 2,3, x,5,8 jest równa 4. Wtedy A. x=2 B. x=3 C. x=4 D. x=5


Zadanie 25. (I pkt) Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 2843. Długość krawędzi podstawy tego graniastosłupa jest równa A. 2 B. 4 C. 8 D. 16


Zadanie 26. (2 pkt) Rozwiąż równanie x +2x —8x-16=0.


Zadanie 27. (2 pkt) Kąt a jest ostry i sina =—— . Oblicz wartość wyrażenia sin” 2 —3cos* a. 43 EJ

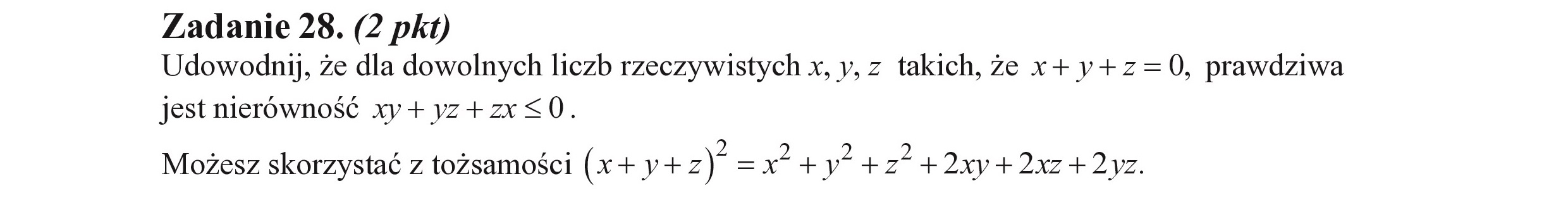
Zadanie 28. (2 pkt) Udowodnij, że dla dowolnych liczb rzeczywistych x, y, z takich, że x+y+z=0, prawdziwa jest nierówność xyv+ yz+zx<0. ME = 3 Możesz skorzystać z tożsamości (x+y+z) =x* +y” +z” +2xy+2xz +2yz. „


Zadanie 29. (2 pkt) Na rysunku przedstawiony jest wykres funkcji f(x) określonej dla x € (-7, 8). Odczytaj z wykresu i zapisz: a) największą wartość funkcji /, b) zbiór rozwiązań nierówności /(x)<0.


Zadanie 30. (2 pkt) Rozwiąż nierówność 2x -7x+520.


Zadanie 31. (2 pkt) Wykaż, że liczba 6" —2-6” +10-6* jest podzielna przez 17.


Zadanie 32. (4 pkt) Punkt S$ jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Kąt ACS jest trzy razy większy od kąta BAS, a kąt CBS jest dwa razy większy od kąta BAS. Oblicz kąty trójkąta ABC. C


Zadanie 33. (4 pkt) Pole podstawy ostrosłupa prawidłowego czworokątnego jest równe 100 cm, a jego pole powierzchni bocznej jest równe 260 cm”. Oblicz objętość tego ostrosłupa.


Zadanie 34. (5 pkt) Dwa miasta łączy linia kolejowa o długości 336 kilometrów. Pierwszy pociąg przebył tę trasę w czasie o 40 minut krótszym niż drugi pociąg. Średnia prędkość pierwszego pociągu na tej trasie była o 9 km/h większa od średniej prędkości drugiego pociągu. Oblicz średnią prędkość każdego z tych pociągów na tej trasie.






























