MATEMATYKA 2011 CZERWIEC MATURA PODSTAWOWA

Zadanie 1. (I pkt) Liczbę 20 można przedstawić w postaci A. 54/2 B. 54/4 245


Zadanie 2. (I pkt) -5 Potęga (>| (gdzie a i b są różne od zera) jest równa 5 > A. -5-7 B. [2] c. a


Zadanie 3. (I pkt) Liczba log, 8 jest równa 2 A. -3 B. a a

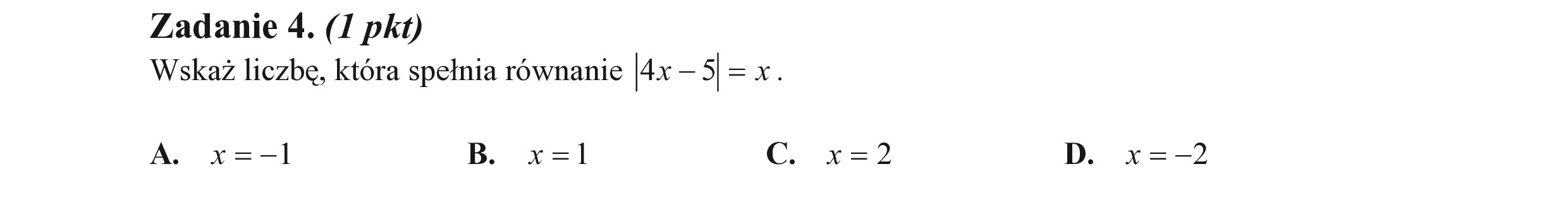
Zadanie 4. (I pkt) Wskaż liczbę, która spełnia równanie dx — 5 =xX. A. x=-l B. x=l1 c.


Zadanie 5. (I pkt) Cenę pewnego towaru najpierw obniżono o 20%, a następnie nową cenę podwyższono o 10%. W wyniku obu tych zmian cena towaru zmniejszyła się w stosunku do pierwotnej o A. 88% B. 15% c. 12% D. 10%

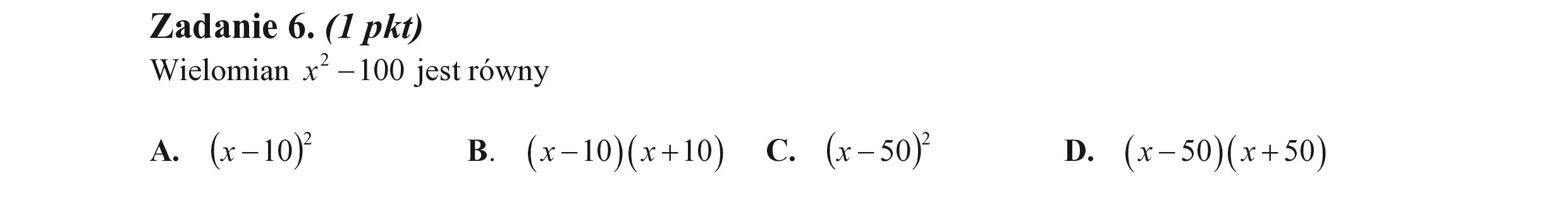
Zadanie 6. (I pkt) Wielomian x* —100 jest równy A. (x-10) B. (x-10)(x+10) C. (x-50) D. (x-50)(x+50)


Zadanie 7. (I pkt) , . x +25 Równanie = IE A. nie ma rozwiązań. B. ma dokładnie jedno rozwiązanie. C. ma dokładnie dwa rozwiązania. D. ma dokładnie trzy rozwiązania.

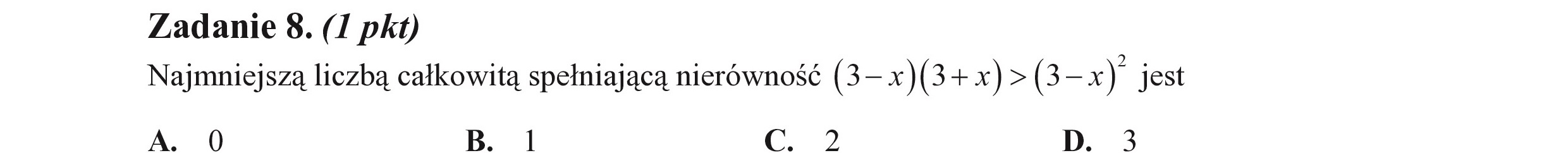
Zadanie 8. (I pkt) Najmniejszą liczbą całkowitą spełniającą nierówność (3— x)(3+ x) >(3-»x) jest A. 0 B. | Cc. 2 D. 3


Zadanie 9. (I pkt) Funkcja liniowa /(x)= x +3 A. jest rosnąca i jej wykres przechodzi przez punkt (0, Śj. B. jest malejąca i jej wykres przechodzi przez punkt (0, —3). Cz D. jest malejąca i jej wykres przechodzi przez punkt (0, 3). jest rosnąca i jej wykres przechodzi przez punkt (0, —3).

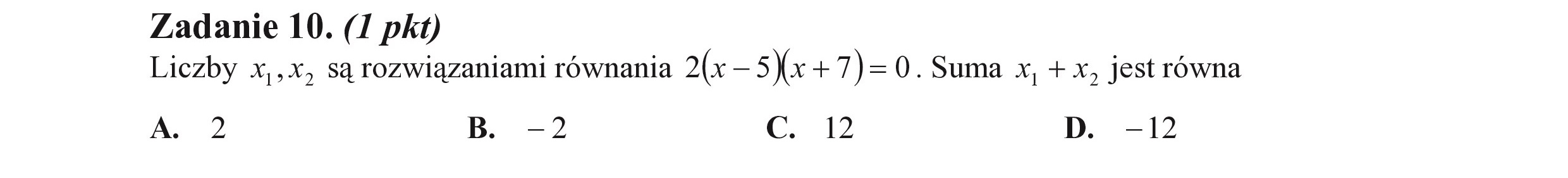
Zadanie 10. (I pkt) Liczby x,,x, są rozwiązaniami równania 2(x s 5) +7)=0. Suma x, + x, jest równa A. 2 B. -2 c. 12 D. -12

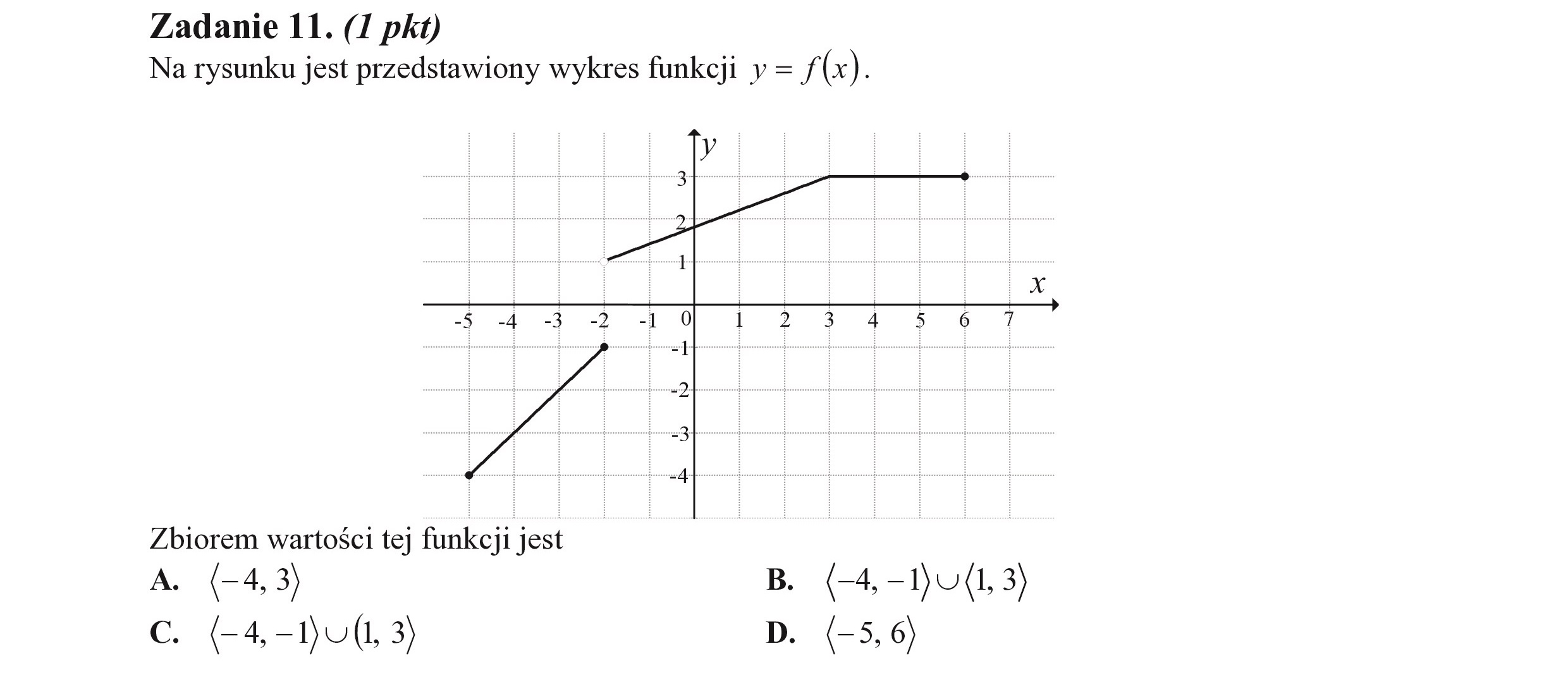
Zadanie 11. (I pkt) Na rysunku jest przedstawiony wykres funkcji y= f (x). Zbiorem wartości tej funkcji jest A. (-4,3) B Cc. (-4,-Dv(1 3) D. (-5,6)

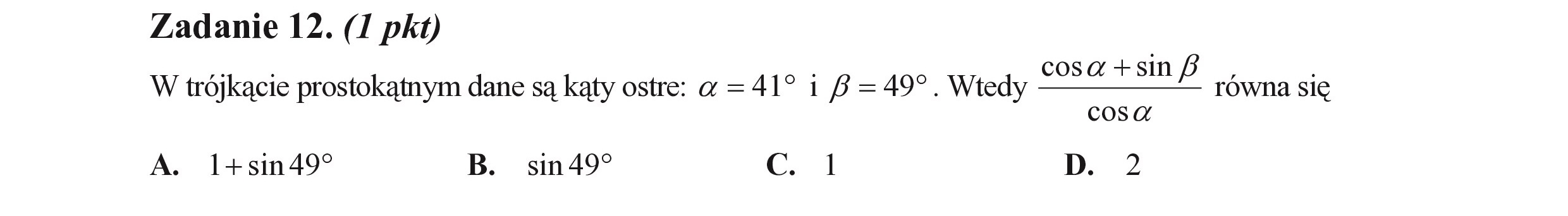
Zadanie 12. (I pkt) ś ; , +gi W trójkącie prostokątnym dane są kąty ostre: a = 41? i 8 = 497. Wtedy gosa + sin f równa się cosa A. 1+sin49? B. sin49? c l D. 2

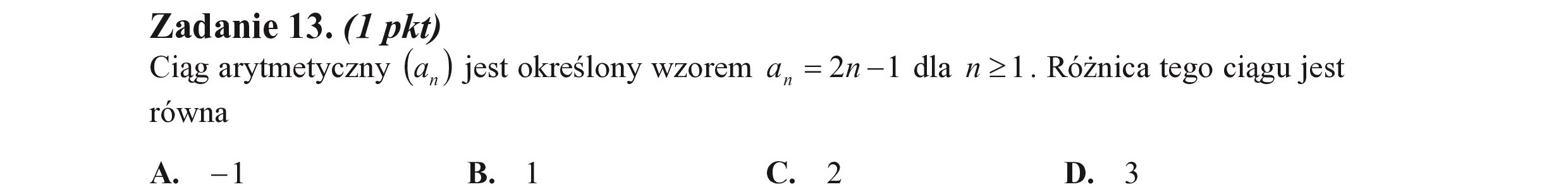
Zadanie 13. (I pkt) Ciąg arytmetyczny (a) jest określony wzorem a, =2n—1 dla n>1. Różnica tego ciągu jest równa A. -1 B. I GG 2 D. 3

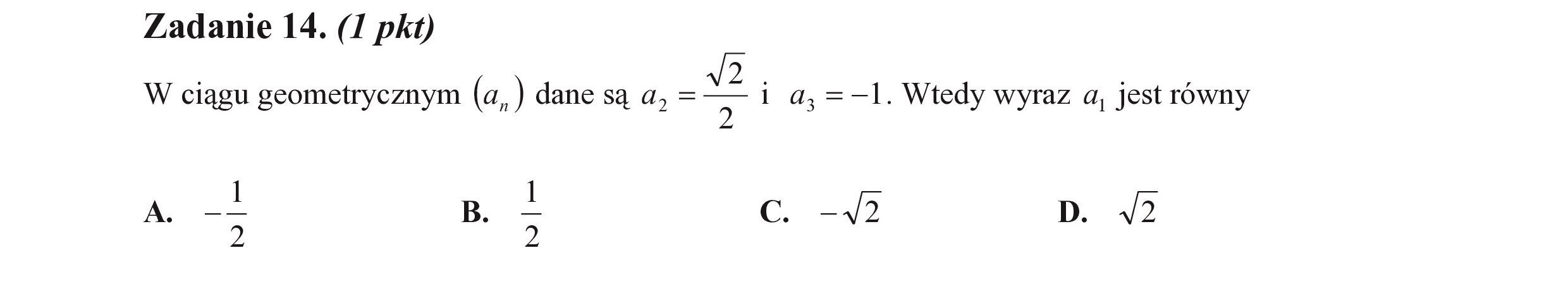
Zadanie 14. (I pkt) Ż . : : W ciągu geometrycznym (a, ) dane są a, = ra i a, =—1. Wtedy wyraz a, jest równy A. -5 B. > Cc. —W2 D. 42

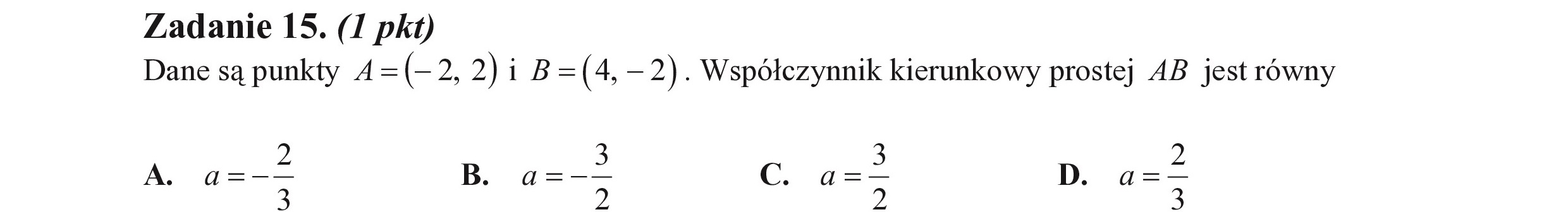
Zadanie 15. (I pkt) Dane są punkty A= (- 2, 2) 1iB= (4. — 2). Współczynnik kierunkowy prostej AB jest równy A. g=—— B. a=-—— CG g=Ć D. a ą 2 3

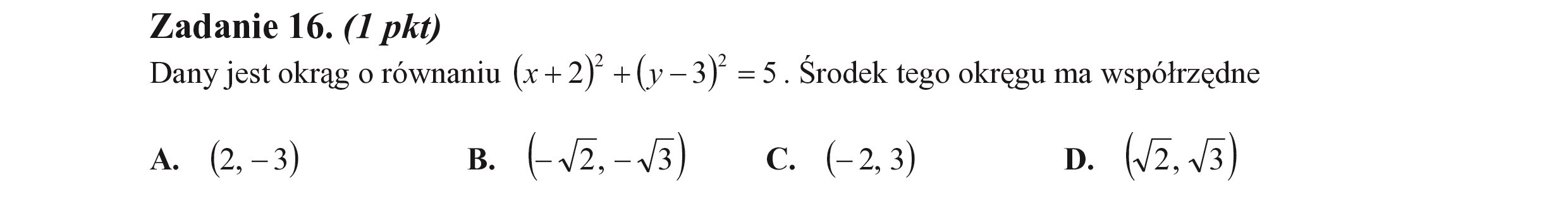
Zadanie 16. (I pkt) Dany jest okrąg o równaniu (x + 2) + (y — 3) = 5. Środek tego okręgu ma współrzędne A. (2,-3) B. 242-493) C. (-23) p. (42,43)


Zadanie 17. (I pkt) Obwód prostokąta jest równy 28. Stosunek długości jego boków jest równy 3:4. Dłuższy bok tego prostokąta jest równy A. 14 B. 8 CG 7 D. 6


Zadanie 18. (I pkt) Dany jest trójkąt prostokątny o przyprostokątnych 6 i 8. Promień okręgu opisanego na tym trójkącie jest równy A. 14 B. 8 Cc Ó D. 5


Zadanie 19. (I pkt) Dane są dwa okręgi o promieniach 12 i 17. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa A. 5 B. 12 CG. 17 D. 29


Zadanie 20. (I pkt) Stożek powstał w wyniku obrotu trójkąta prostokątnego o przyprostokątnych 6 i 13 wokół krótszej przyprostokątnej. Promień podstawy tego stożka jest równy A. 6 B. 13 C. 6,6 D. 3

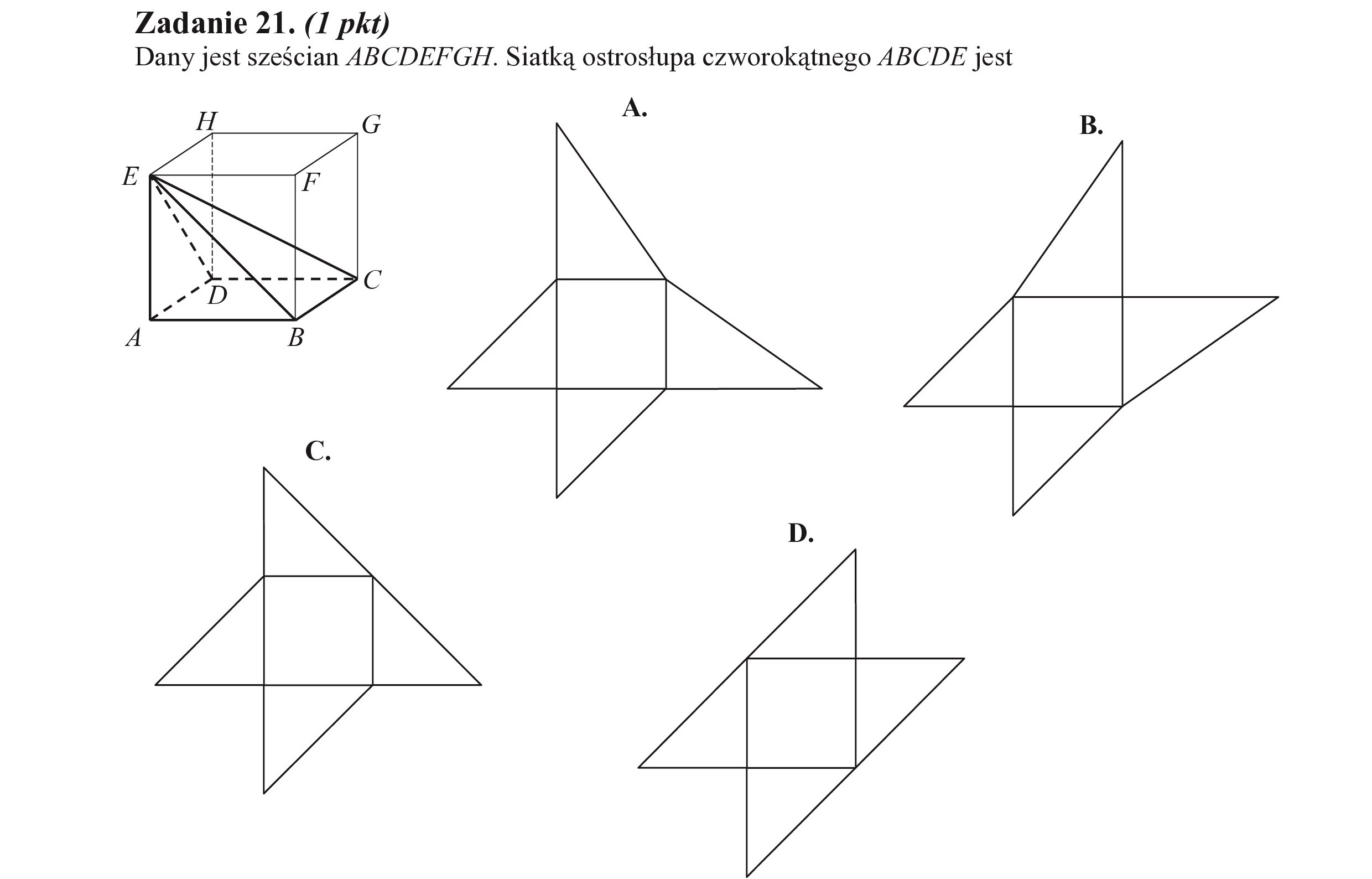
Zadanie 21. (I pkt) Dany jest sześcian ABCDEFGH. Siatką ostrosłupa czworokątnego ABCDE jest A.


Zadanie 22. (I pkt) Jeżeli A jest zdarzeniem losowym takim, że P(4)=6-P(4'), oraz A' jest zdarzeniem przeciwnym do zdarzenia A, to prawdopodobieństwo zdarzenia A jest równe NE B. — e p. 5 6 6 jj 7


Zadanie 23. (2 pkt) Rozwiąż nierówność 2x +2x4+24>0,

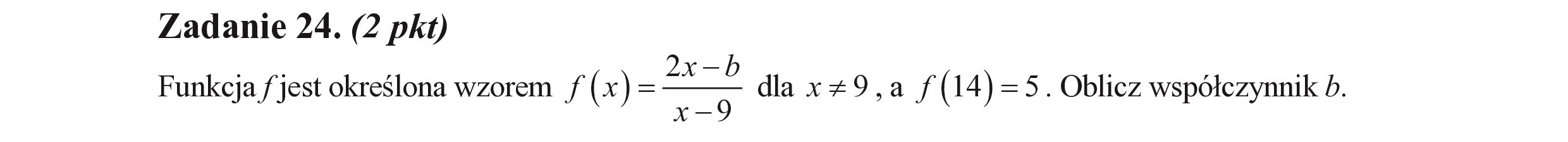
Zadanie 24. (2 pkt) = ŻX Funkcja f jest określona wzorem /(x)= x-9 m dla x =9,a /(14)=5. Oblicz współczynnik b.

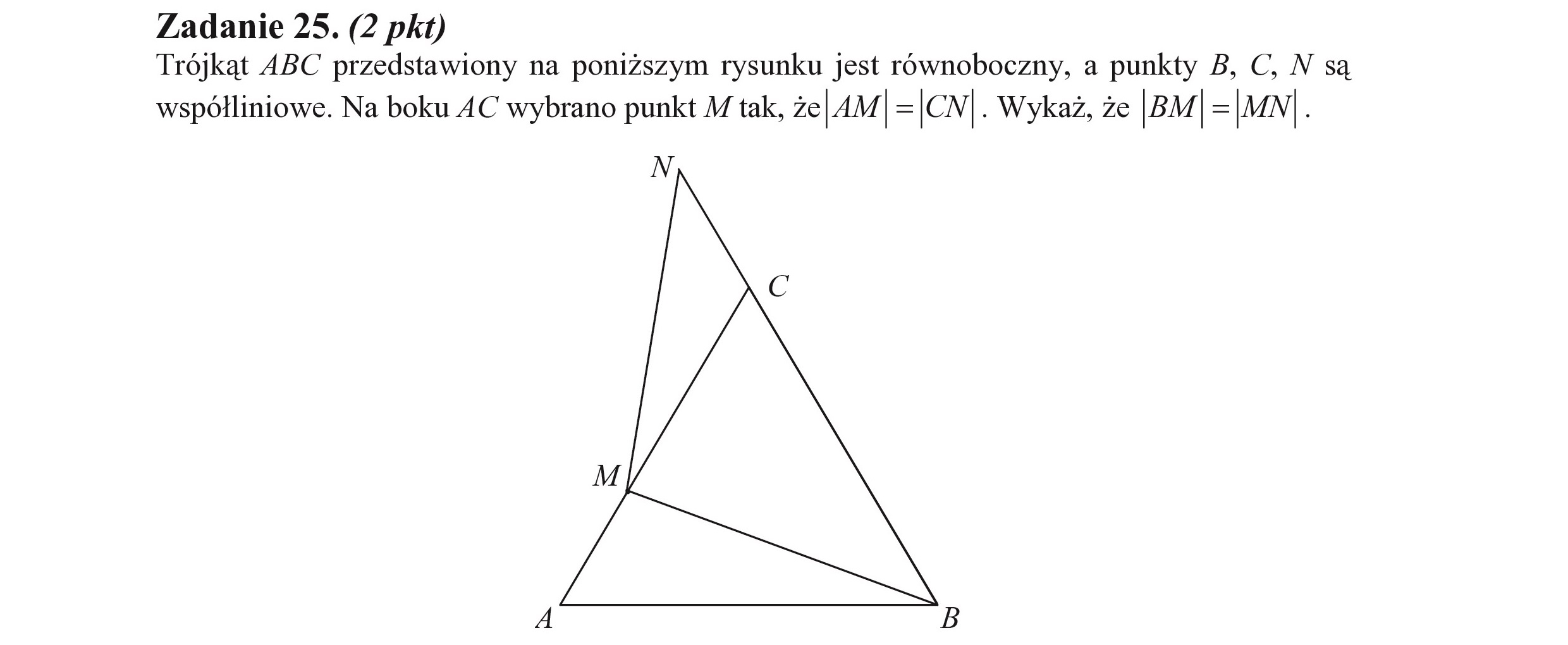
Zadanie 25. (2 pkt) Trójkąt ABC przedstawiony na poniższym rysunku jest równoboczny, a punkty B, C, N są współliniowe. Na boku AC wybrano punkt M tak, że|AM | = |CN | . Wykaż, że |BM | = |MN | 3 N

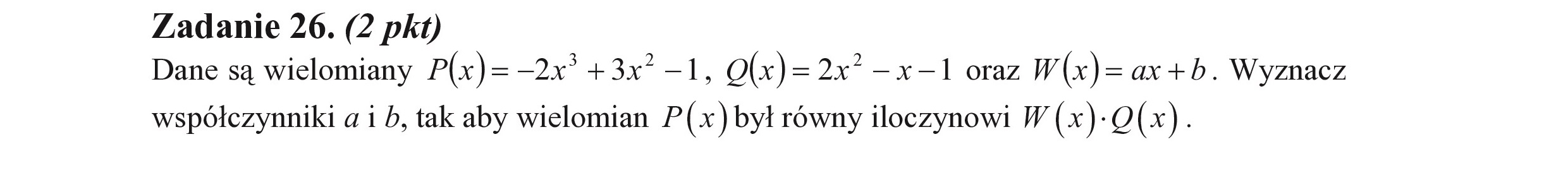
Zadanie 26. (2 pkt) Dane są wielomiany P(x)=—2x +3x -1, Q(x)=2x* —x-1 oraz W(x)=ax+b. Wyznacz współczynniki a i b, tak aby wielomian P(x ) był równy iloczynowi W (x)-O(x).

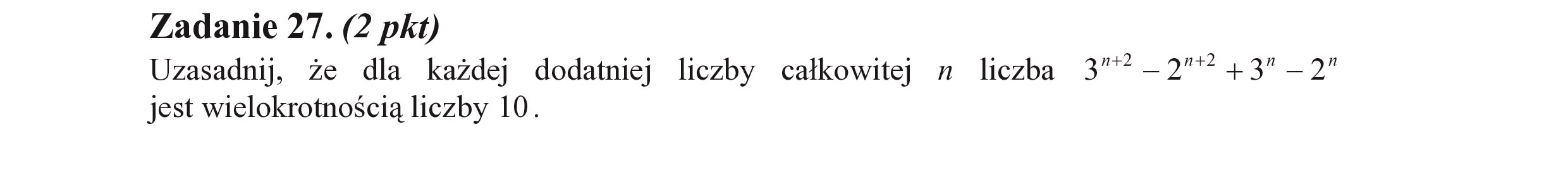
Zadanie 27. (2 pkt) Uzasadnij, że dla każdej dodatniej liczby całkowitej mn liczba 37-27 +3" -2" jest wielokrotnością liczby 10.


Zadanie 28. (2 pkt) Tabela przedstawia wyniki uzyskane na sprawdzianie przez uczniów klasy III. Oceny Liczba uczniów Oblicz medianę i średnią arytmetyczną uzyskanych ocen.


Zadanie 29. (2 pkt) Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że liczba oczek w pierwszym rzucie jest o I mniejsza od liczby oczek w drugim rzucie.


Zadanie 30. (2 pkt) Liczby 27, x,3 są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz ósmy wyraz tego ciągu.


Zadanie 31. (4 pkt) Oblicz sumę wszystkich liczb trzycyfrowych zapisanych wyłącznie za pomocą cyfr 1, 2, 3, 4 (cyfry mogą się powtarzać).


Zadanie 32. (4 pkt) Podstawą ostrosłupa ABCDS jest romb ABCD o boku długości 4. Kąt ABC rombu ma miarę 120%, |ASJ=|CS|=10 i |BS|=|DS|. Oblicz sinus kąta nachylenia krawędzi BS do płaszczyzny podstawy ostrosłupa.


Zadanie 33. (4 pkt) Wyznacz równanie okręgu przechodzącego przez punkt A= (I, 8) i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.

MATEMATYKA 2011 CZERWIEC MATURA PODSTAWOWA

Zadanie 1. (I pkt) Liczbę 20 można przedstawić w postaci A. 54/2 B. 54/4 245


Zadanie 2. (I pkt) -5 Potęga (>| (gdzie a i b są różne od zera) jest równa 5 > A. -5-7 B. [2] c. a


Zadanie 3. (I pkt) Liczba log, 8 jest równa 2 A. -3 B. a a

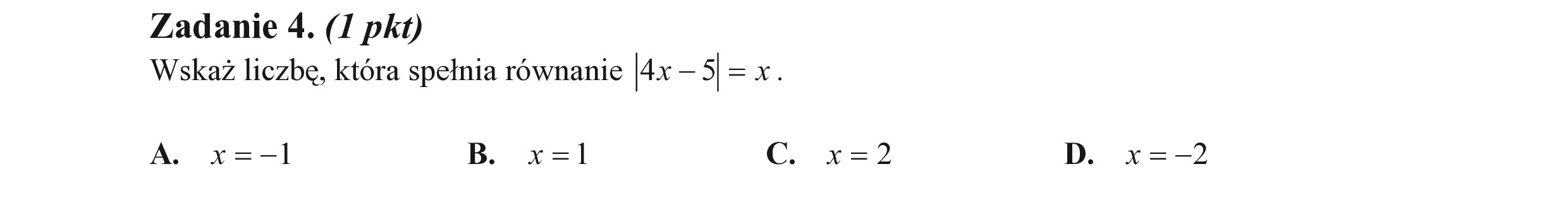
Zadanie 4. (I pkt) Wskaż liczbę, która spełnia równanie dx — 5 =xX. A. x=-l B. x=l1 c.


Zadanie 5. (I pkt) Cenę pewnego towaru najpierw obniżono o 20%, a następnie nową cenę podwyższono o 10%. W wyniku obu tych zmian cena towaru zmniejszyła się w stosunku do pierwotnej o A. 88% B. 15% c. 12% D. 10%

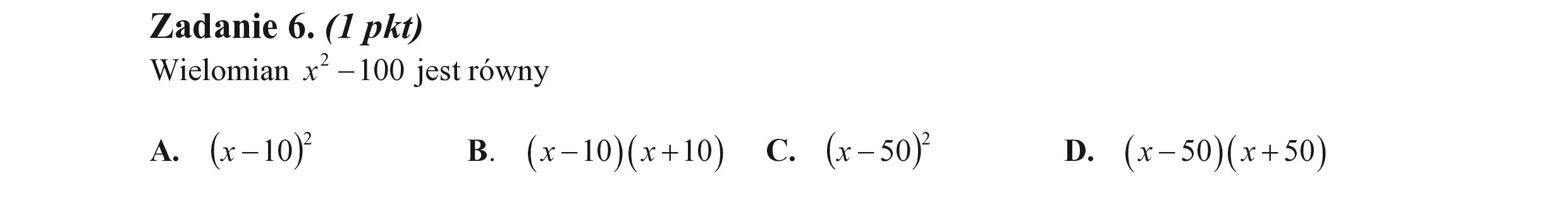
Zadanie 6. (I pkt) Wielomian x* —100 jest równy A. (x-10) B. (x-10)(x+10) C. (x-50) D. (x-50)(x+50)


Zadanie 7. (I pkt) , . x +25 Równanie = IE A. nie ma rozwiązań. B. ma dokładnie jedno rozwiązanie. C. ma dokładnie dwa rozwiązania. D. ma dokładnie trzy rozwiązania.

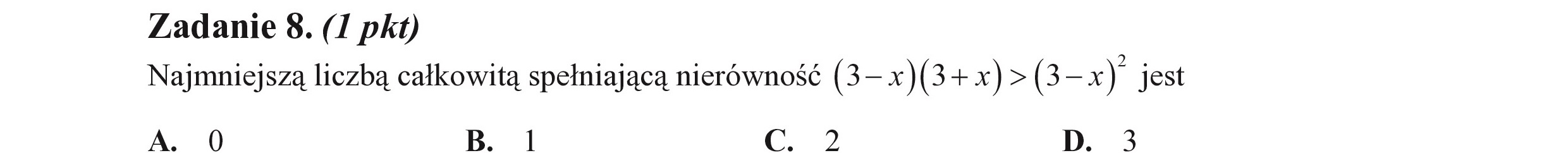
Zadanie 8. (I pkt) Najmniejszą liczbą całkowitą spełniającą nierówność (3— x)(3+ x) >(3-»x) jest A. 0 B. | Cc. 2 D. 3


Zadanie 9. (I pkt) Funkcja liniowa /(x)= x +3 A. jest rosnąca i jej wykres przechodzi przez punkt (0, Śj. B. jest malejąca i jej wykres przechodzi przez punkt (0, —3). Cz D. jest malejąca i jej wykres przechodzi przez punkt (0, 3). jest rosnąca i jej wykres przechodzi przez punkt (0, —3).

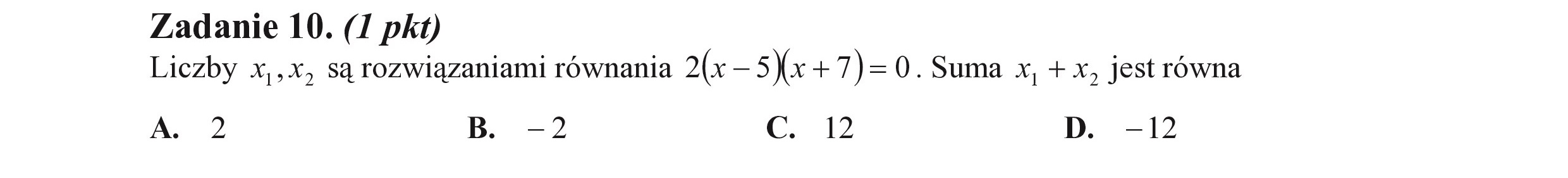
Zadanie 10. (I pkt) Liczby x,,x, są rozwiązaniami równania 2(x s 5) +7)=0. Suma x, + x, jest równa A. 2 B. -2 c. 12 D. -12


Zadanie 11. (I pkt) Na rysunku jest przedstawiony wykres funkcji y= f (x). Zbiorem wartości tej funkcji jest A. (-4,3) B Cc. (-4,-Dv(1 3) D. (-5,6)

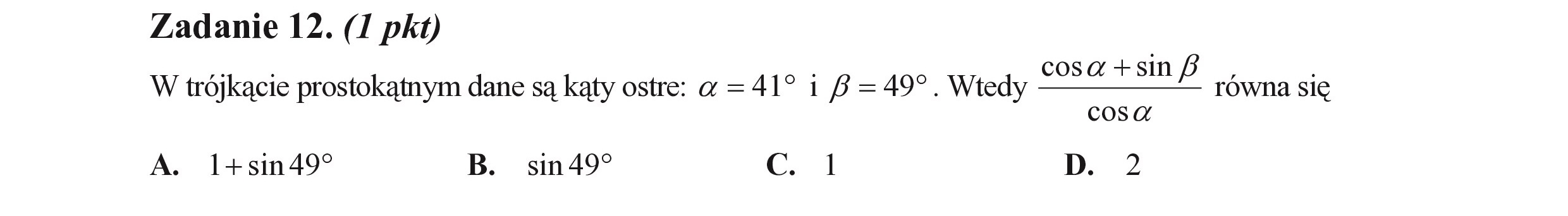
Zadanie 12. (I pkt) ś ; , +gi W trójkącie prostokątnym dane są kąty ostre: a = 41? i 8 = 497. Wtedy gosa + sin f równa się cosa A. 1+sin49? B. sin49? c l D. 2

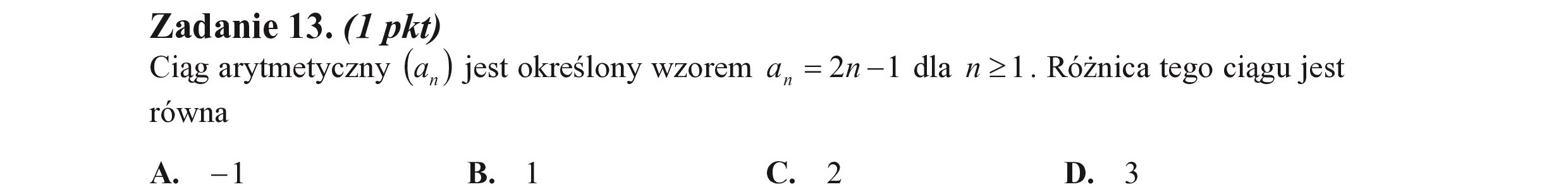
Zadanie 13. (I pkt) Ciąg arytmetyczny (a) jest określony wzorem a, =2n—1 dla n>1. Różnica tego ciągu jest równa A. -1 B. I GG 2 D. 3

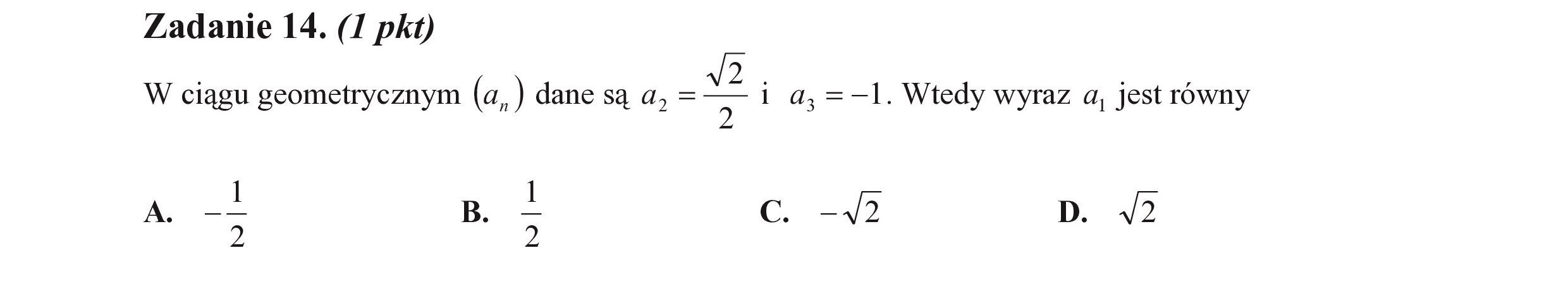
Zadanie 14. (I pkt) Ż . : : W ciągu geometrycznym (a, ) dane są a, = ra i a, =—1. Wtedy wyraz a, jest równy A. -5 B. > Cc. —W2 D. 42

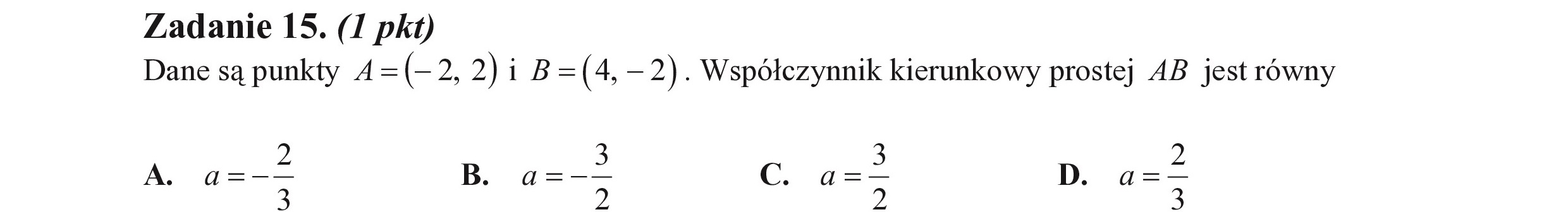
Zadanie 15. (I pkt) Dane są punkty A= (- 2, 2) 1iB= (4. — 2). Współczynnik kierunkowy prostej AB jest równy A. g=—— B. a=-—— CG g=Ć D. a ą 2 3

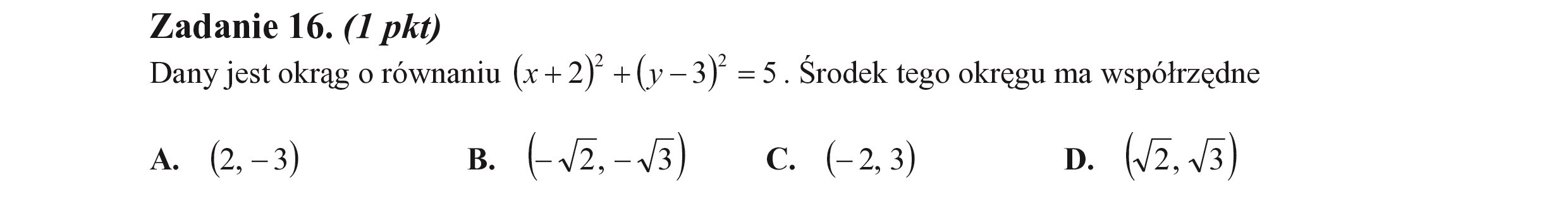
Zadanie 16. (I pkt) Dany jest okrąg o równaniu (x + 2) + (y — 3) = 5. Środek tego okręgu ma współrzędne A. (2,-3) B. 242-493) C. (-23) p. (42,43)


Zadanie 17. (I pkt) Obwód prostokąta jest równy 28. Stosunek długości jego boków jest równy 3:4. Dłuższy bok tego prostokąta jest równy A. 14 B. 8 CG 7 D. 6


Zadanie 18. (I pkt) Dany jest trójkąt prostokątny o przyprostokątnych 6 i 8. Promień okręgu opisanego na tym trójkącie jest równy A. 14 B. 8 Cc Ó D. 5


Zadanie 19. (I pkt) Dane są dwa okręgi o promieniach 12 i 17. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa A. 5 B. 12 CG. 17 D. 29


Zadanie 20. (I pkt) Stożek powstał w wyniku obrotu trójkąta prostokątnego o przyprostokątnych 6 i 13 wokół krótszej przyprostokątnej. Promień podstawy tego stożka jest równy A. 6 B. 13 C. 6,6 D. 3


Zadanie 21. (I pkt) Dany jest sześcian ABCDEFGH. Siatką ostrosłupa czworokątnego ABCDE jest A.


Zadanie 22. (I pkt) Jeżeli A jest zdarzeniem losowym takim, że P(4)=6-P(4'), oraz A' jest zdarzeniem przeciwnym do zdarzenia A, to prawdopodobieństwo zdarzenia A jest równe NE B. — e p. 5 6 6 jj 7


Zadanie 23. (2 pkt) Rozwiąż nierówność 2x +2x4+24>0,

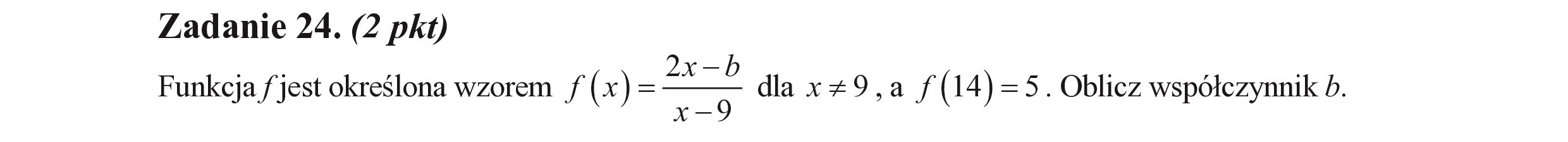
Zadanie 24. (2 pkt) = ŻX Funkcja f jest określona wzorem /(x)= x-9 m dla x =9,a /(14)=5. Oblicz współczynnik b.


Zadanie 25. (2 pkt) Trójkąt ABC przedstawiony na poniższym rysunku jest równoboczny, a punkty B, C, N są współliniowe. Na boku AC wybrano punkt M tak, że|AM | = |CN | . Wykaż, że |BM | = |MN | 3 N

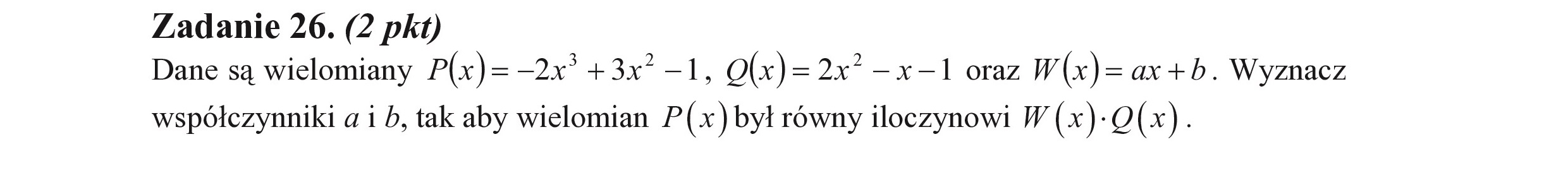
Zadanie 26. (2 pkt) Dane są wielomiany P(x)=—2x +3x -1, Q(x)=2x* —x-1 oraz W(x)=ax+b. Wyznacz współczynniki a i b, tak aby wielomian P(x ) był równy iloczynowi W (x)-O(x).

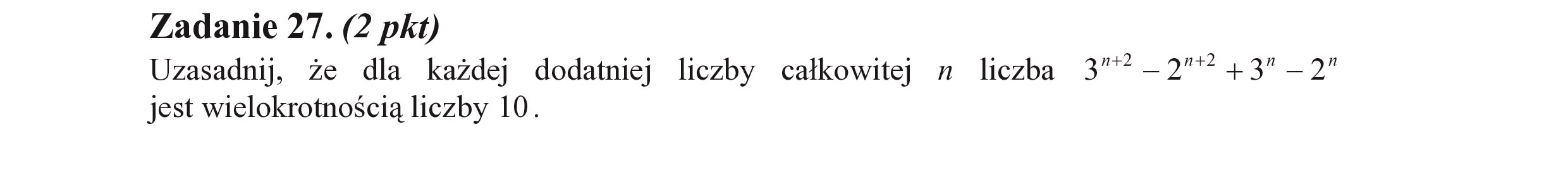
Zadanie 27. (2 pkt) Uzasadnij, że dla każdej dodatniej liczby całkowitej mn liczba 37-27 +3" -2" jest wielokrotnością liczby 10.


Zadanie 28. (2 pkt) Tabela przedstawia wyniki uzyskane na sprawdzianie przez uczniów klasy III. Oceny Liczba uczniów Oblicz medianę i średnią arytmetyczną uzyskanych ocen.


Zadanie 29. (2 pkt) Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że liczba oczek w pierwszym rzucie jest o I mniejsza od liczby oczek w drugim rzucie.


Zadanie 30. (2 pkt) Liczby 27, x,3 są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz ósmy wyraz tego ciągu.


Zadanie 31. (4 pkt) Oblicz sumę wszystkich liczb trzycyfrowych zapisanych wyłącznie za pomocą cyfr 1, 2, 3, 4 (cyfry mogą się powtarzać).


Zadanie 32. (4 pkt) Podstawą ostrosłupa ABCDS jest romb ABCD o boku długości 4. Kąt ABC rombu ma miarę 120%, |ASJ=|CS|=10 i |BS|=|DS|. Oblicz sinus kąta nachylenia krawędzi BS do płaszczyzny podstawy ostrosłupa.


Zadanie 33. (4 pkt) Wyznacz równanie okręgu przechodzącego przez punkt A= (I, 8) i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.






























