Graficzna prezentacja zbiorów

Zbiór to uporządkowany zbiór elementów. Zapisujemy go w nawiasach klamrowych, np. Zbiór A = {1, 2, 3}.

Suma (A ∪ B) to wszystkie elementy, które należą przynajmniej do jednego ze zbiorów.

Iloczyn (A ∩ B) to elementy wspólne dla obu zbiorów.

Różnica (A \ B) to elementy, które są w A, ale nie w B.

Zbiór pusty (∅) to zbiór bez żadnych elementów.

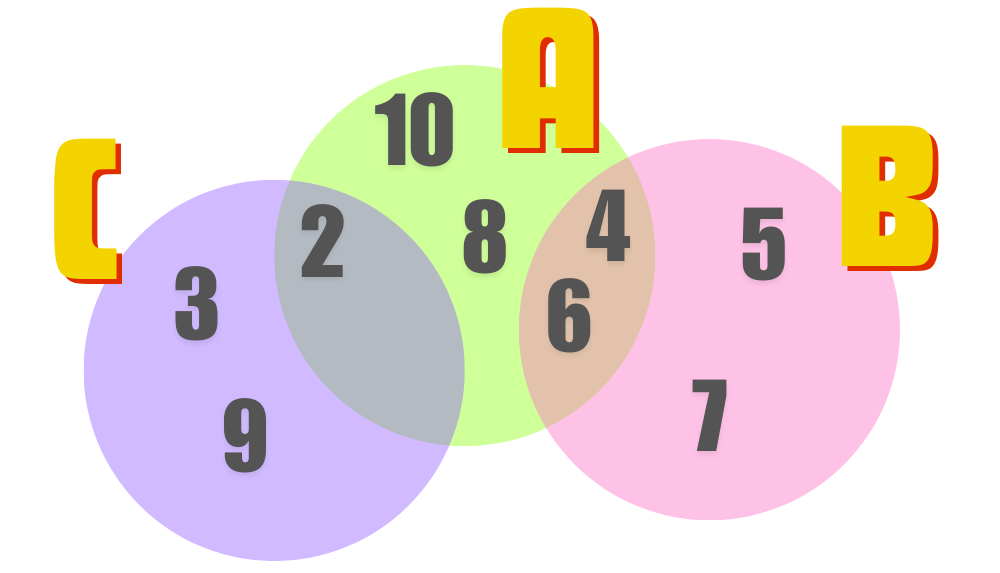
Zbiór A = {2, 4, 6, 8, 10}

Zbiór B = {4, 5, 6, 7}

Zbiór C = {2, 3, 9}

Przykład operacji na zbiorach
Zbiory A oraz B Zbiory A oraz C Zbiory B oraz C
  • A ∪ B = {2, 4, 5, 6, 7, 8, 10}
  • A ∩ B = {4, 6}
  • A \ B = {2, 8, 10}
  • B \ A = {5, 7}
  • A ∪ C = {2, 3, 4, 6, 8, 9, 10}
  • A ∩ C = {2}
  • A \ C = {3, 4, 6, 8, 10}
  • C \ A = {3, 9}
  • B ∪ C = {2, 3, 4, 5, 6, 7, 9}
  • B ∩ C = ∅
  • B \ C = {4, 5, 6, 7}
  • C \ B = {2, 3, 9}