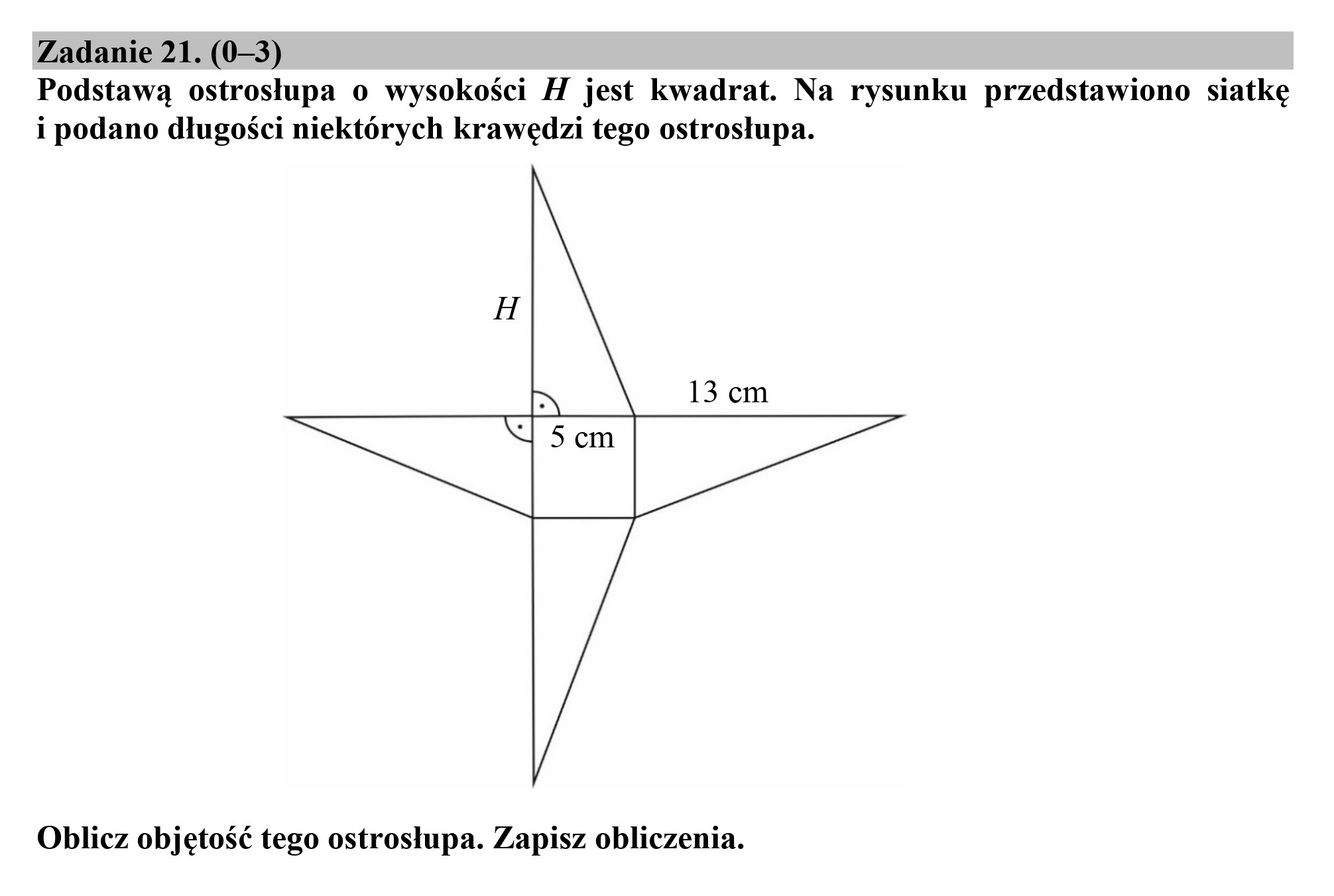
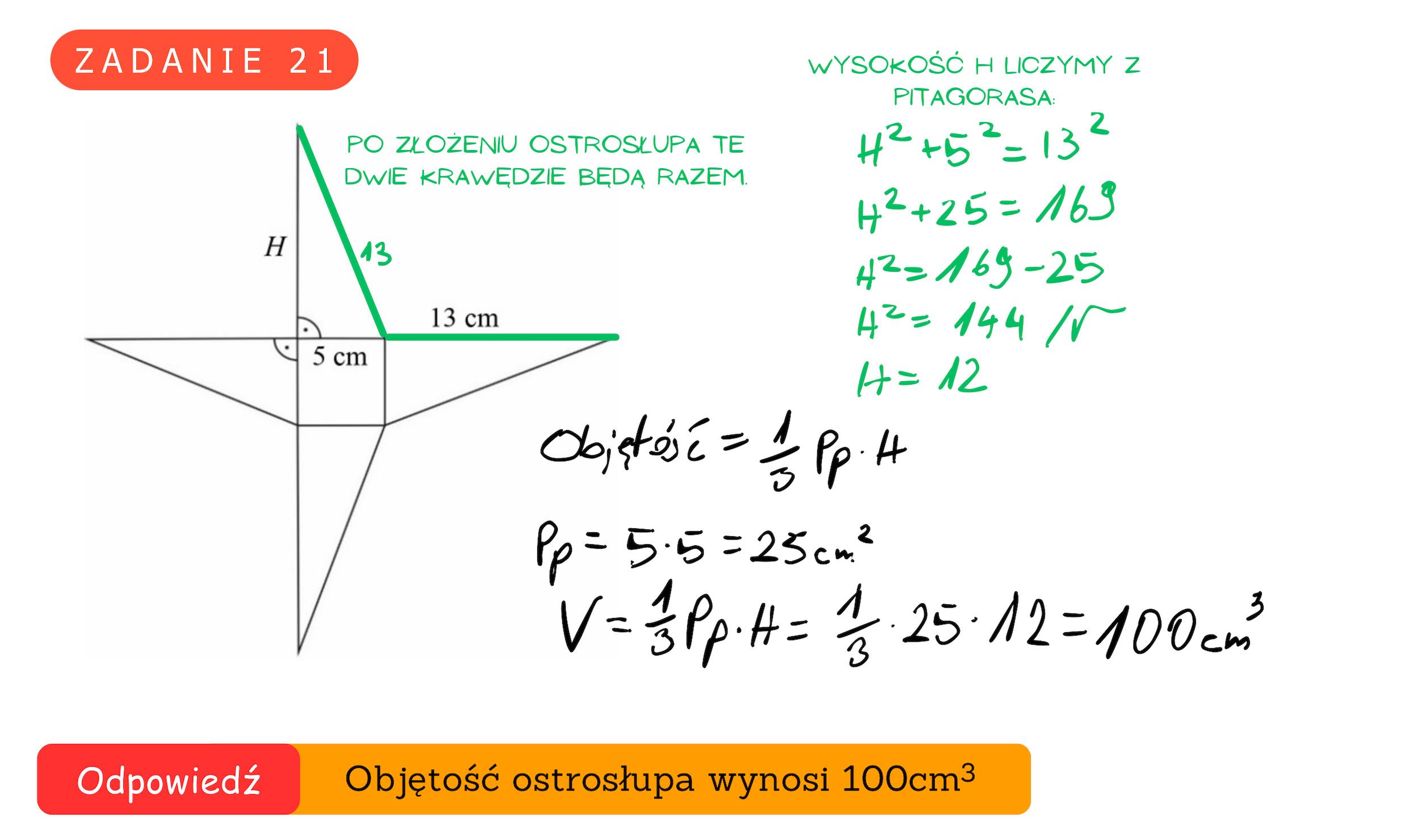
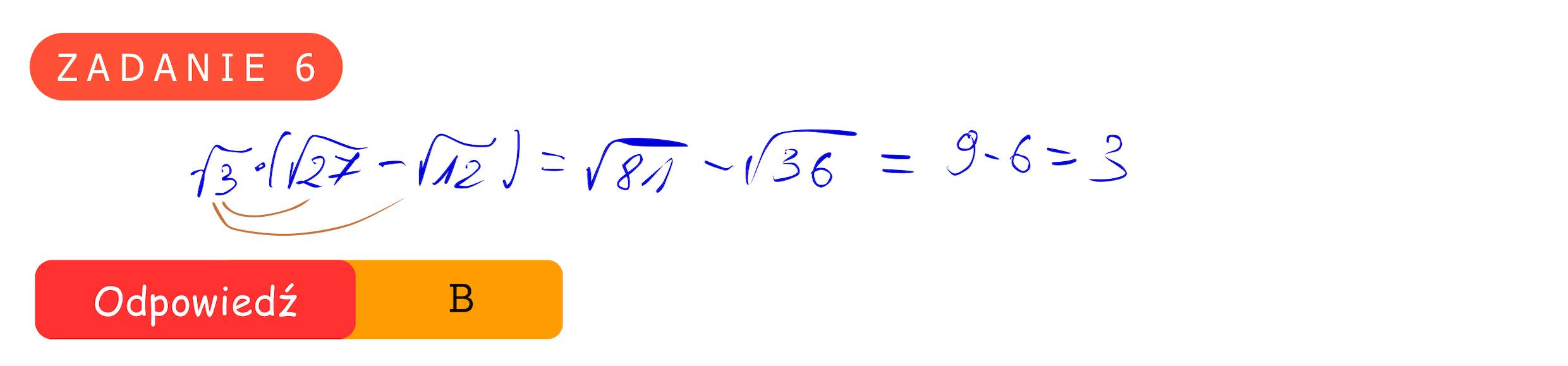EGZAMIN ÓSMOKLASISTY Z MATEMATYKI - TERMIN GŁÓWNY 2020
100%



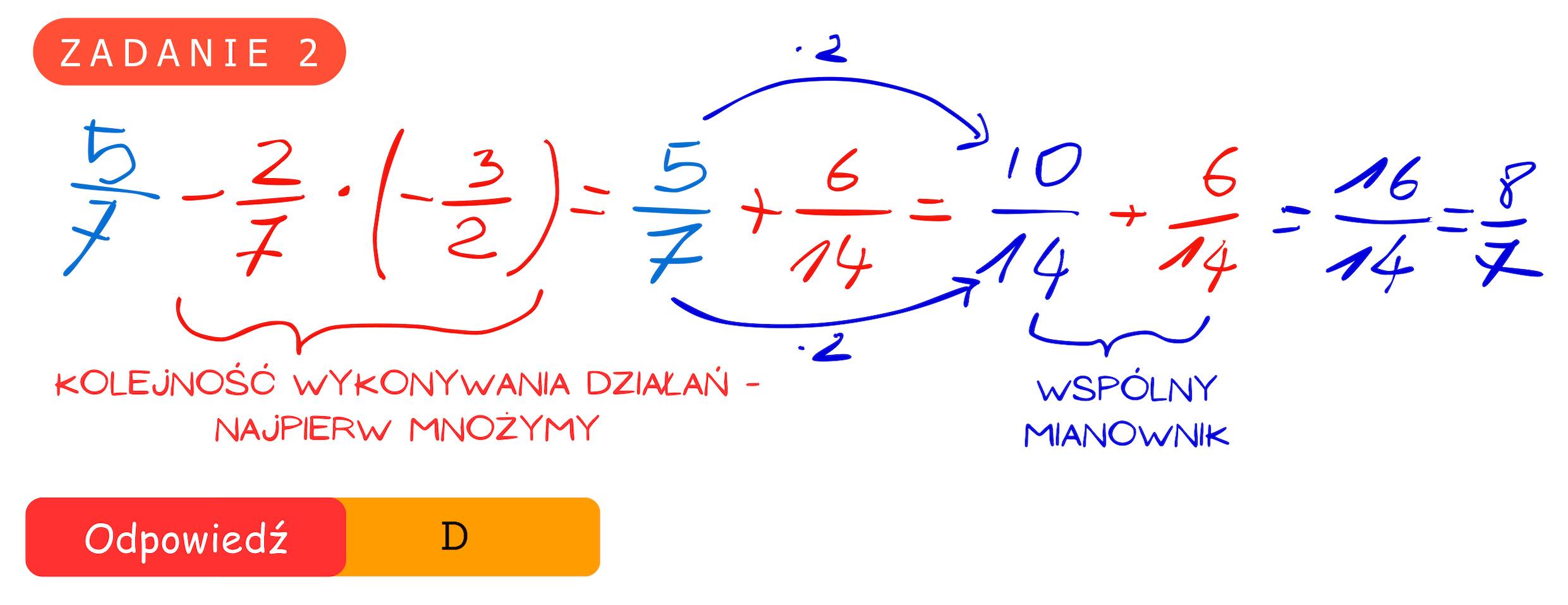

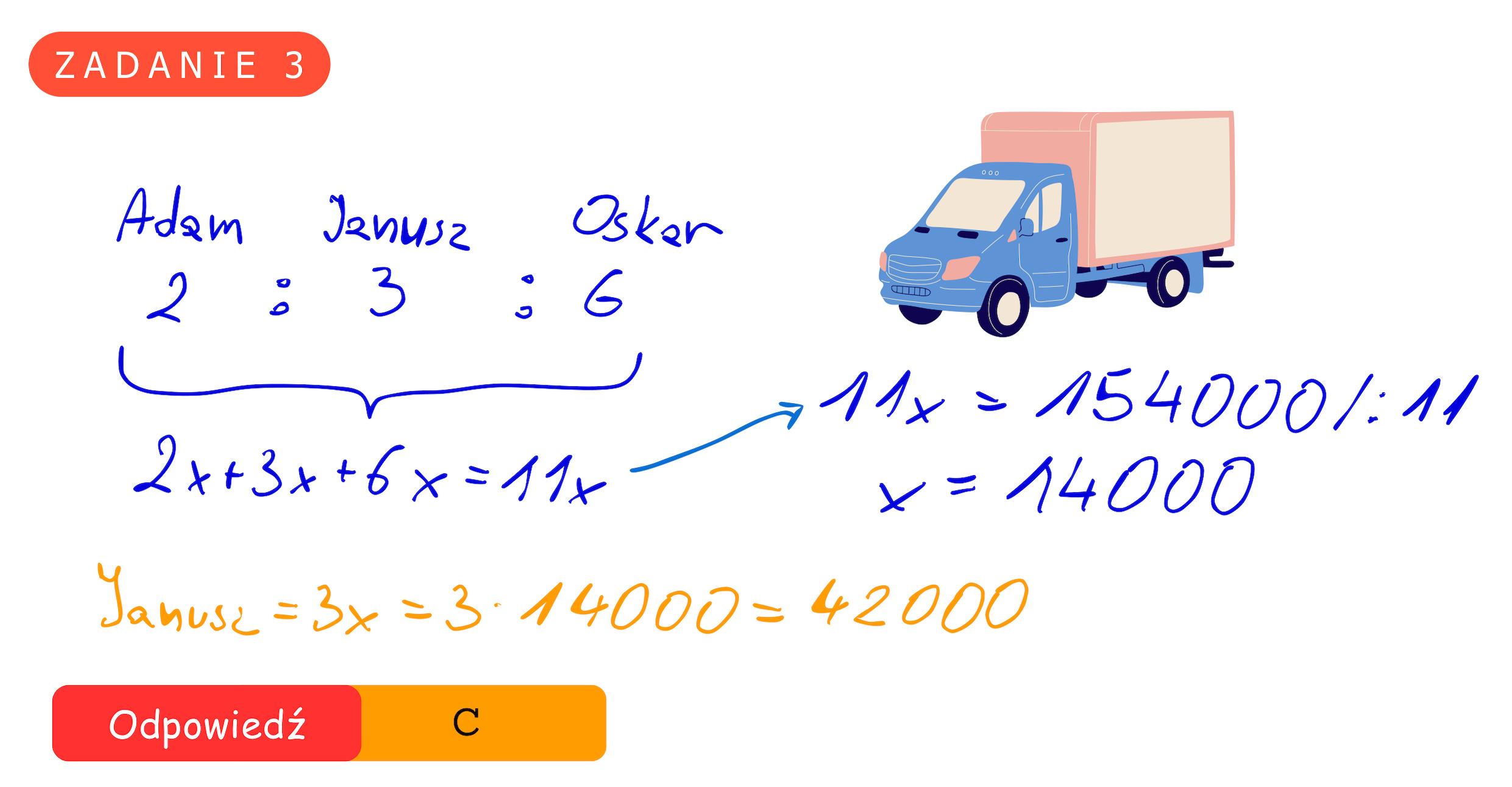


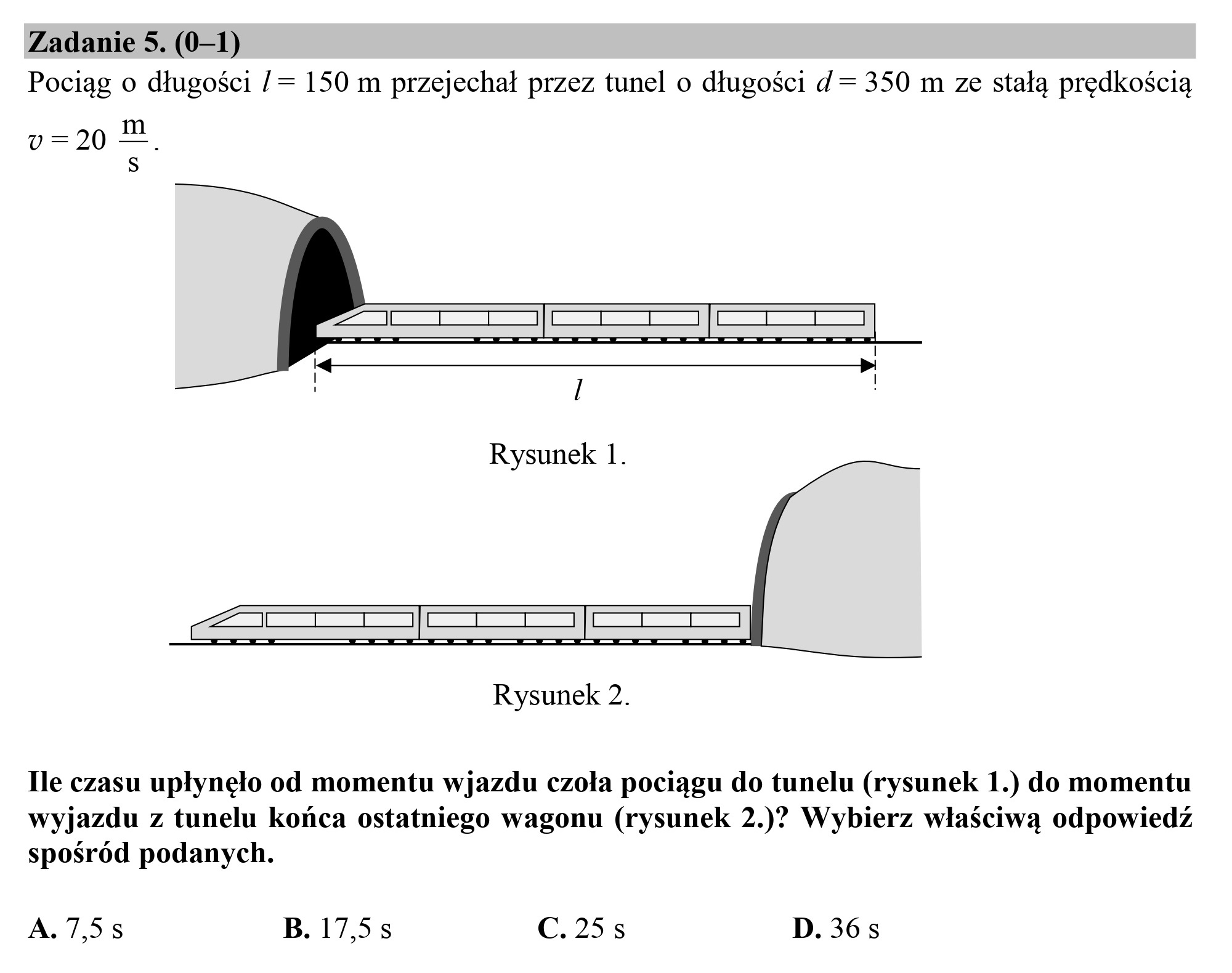















EGZAMIN ÓSMOKLASISTY Z MATEMATYKI - TERMIN GŁÓWNY 2020
100%