EGZAMIN ÓSMOKLASISTY Z MATEMATYKI - TERMIN GŁÓWNY 2024
100%




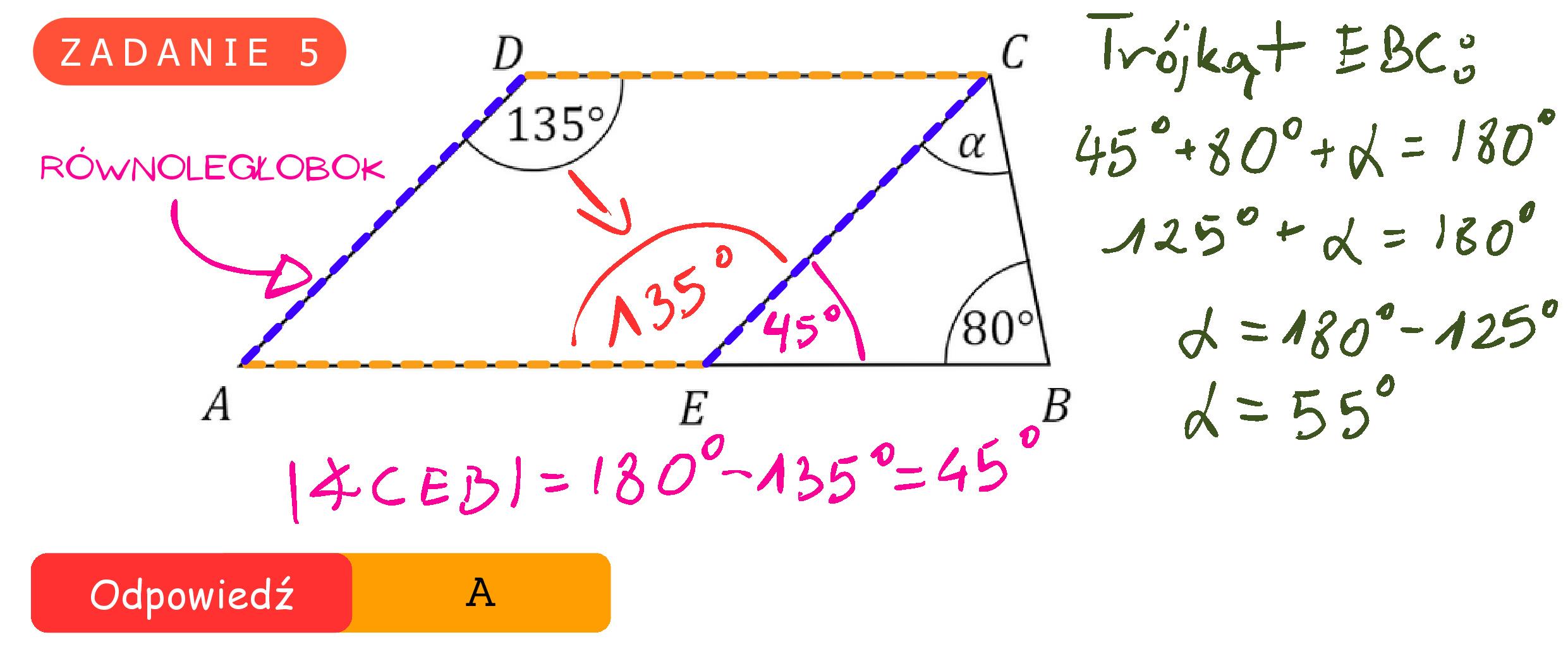
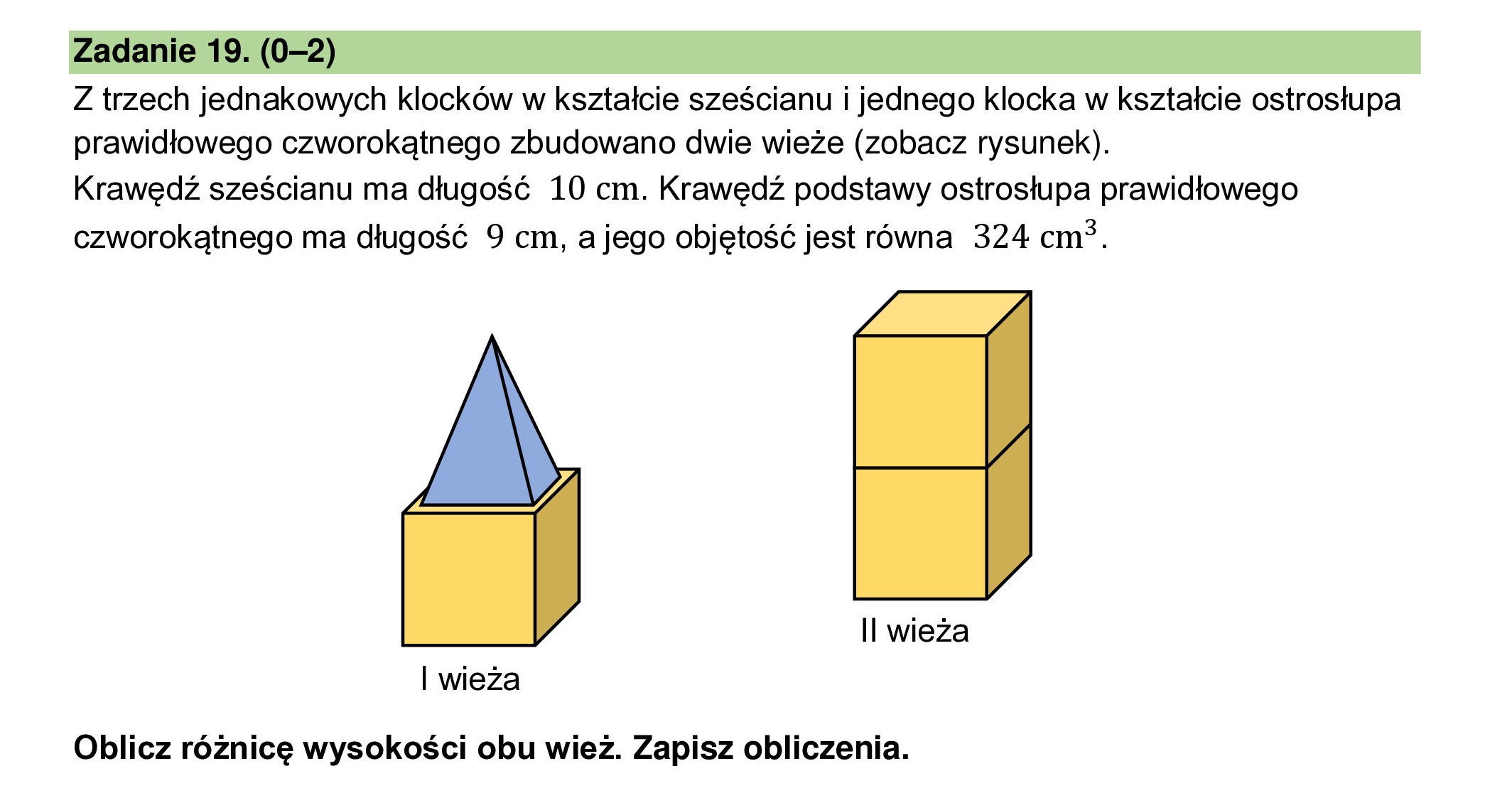
![Dany jest trapez ABCD, w którym bok AB jest równoległy do boku DC. W tym trapezie
poprowadzono odcinek EC równoległy do boku AD, podano miary dwóch kątów oraz
oznaczono kąt a (zobacz rysunek).
D C
G35) Ga]
80?
A E B
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt a ma miarę
A. 557 B. 50? C. 459 D. 20?](https://firebasestorage.googleapis.com/v0/b/zdalnaszkola-images.appspot.com/o/egzamin_%C3%B3smoklasisty%2F2024_EGZAMIN_ZADANIE_5.jpg?alt=media)









EGZAMIN ÓSMOKLASISTY Z MATEMATYKI - TERMIN GŁÓWNY 2024
100%







![Dany jest trapez ABCD, w którym bok AB jest równoległy do boku DC. W tym trapezie
poprowadzono odcinek EC równoległy do boku AD, podano miary dwóch kątów oraz
oznaczono kąt a (zobacz rysunek).
D C
G35) Ga]
80?
A E B
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt a ma miarę
A. 557 B. 50? C. 459 D. 20?](https://firebasestorage.googleapis.com/v0/b/zdalnaszkola-images.appspot.com/o/egzamin_%C3%B3smoklasisty%2F2024_EGZAMIN_ZADANIE_5.jpg?alt=media)